au sommaire
- À lire aussi
La découverte du boson de Higgs au Cern s'inscrit dans une étude du monde au niveau fondamental, où les symétries jouent un rôle essentiel. © Cern
L'élégante efficacité des symétries
Les symétries sont au cœur de la physique et des mathématiques. En saisissant l'essentiel, elles nous aident par exemple à comprendre les propriétés qui émergentémergent à grande échelle quand un nombre important d'éléments interagissent.
Les symétries, entre harmonie et esthétisme
Il y a longtemps que la notion de symétrie est intimement liée à l'esthétique. Le mot, mais certainement pas l'idée, tacitement présente dans les artefacts et même dans les mythes les plus anciens conservés par la mémoire humaine, est issu du grec -- sum (avec, accord) metron (mesure, proportion) -- et sera repris en latin par le mot « commensurable ».
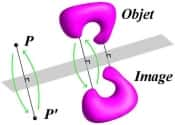
La symétrie miroir, une symétrie du quotidien
Pour en revenir à l'esthétique, en particulier dans les arts plastiquesplastiques, commençons par un peu de géométrie. L'une des symétries les plus naturelles est sans doute la symétrie miroir ou symétrie plane. À chaque point P d'un objet, on associe son image P' par un miroir plan, appelé plan de symétrie.
Les quatre facettes de la notion de symétrie
Pour tenter de comprendre les raisons du rôle cardinal joué par les symétries en physique, il nous faut d'abord préciser les multiples sens que recouvre la notion de symétrie. En s'en emparant, les physiciensphysiciens ont donné à celle-ci une envergure considérable au fur et à mesure que l'on découvrait, tout au long du XXe siècle, sa féconditéfécondité et sa pertinence.
Les mathématiques derrière les symétries
Mathématiquement, les correspondances qui définissent une symétrie se traduisent par des applications TT : E → E internes à l'ensemble E des éléments que l'on cherche à décrire.
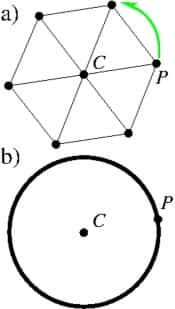
Exemples de transformations de symétrie
Les transformations géométriques comme la symétrie miroir ou une rotation s'appuient exclusivement sur l'espace sans jamais faire intervenir le facteur temps. Les physiciens enrichissent cette panoplie de transformations en lui ajoutant des transformations dépendantes du temps (transformations dynamiques).
Invariance et transformations : d'un rôle descriptif à un rôle constructif
Par constructionconstruction, chaque classe S est un ensemble invariant sous l'action de la transformation T. Mais les règles qui définissent T ne sont pas forcément connues à priori.
Les symétries, outil transdisciplinaire
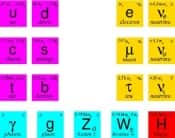
Des grottes de Blombos aux souterrains du Cern où a été découvert le boson de Higgsboson de Higgs (pierre angulaire du modèle standardmodèle standard des particules élémentairesparticules élémentaires construit essentiellement sur la notion de groupe de symétrie), les symétries et les notions intimement reliées à elles forment une matrice indispensable à toute forme de pensée.
Pour aller plus loin : les ouvrages d’Amaury Mouchet
Nous vous recommandons la lecture de L'élégante efficacité des symétries, un ouvrage d'Amaury MouchetAmaury Mouchet, aux éditions Dunod. Pour en savoir plus sur la physique quantiquephysique quantique, découvrez également L'étrange subtilité quantique, du même auteur.