Visitez les multivers de Max Tegmark : les univers parallèles d'Everett

Le multivers de niveau III est probablement celui qui fascine le plus Max Tegmark, avec celui de niveau IV, et pas seulement parce qu'il semble émerger des travaux fondateurs de Erwin SchrödingerErwin Schrödinger en mécanique quantique, l'un des physiciensphysiciens que Tegmark admire particulièrement avec Richard FeynmanRichard Feynman et John Wheeler. Une admiration compréhensible car Schrödinger était un esprit foncièrement original dont la pensée embrassait de vastes domaines. Beaucoup connaissent la fameuse équation portant son nom et qu'il a découverte en 1926. Mais peu, sans doute, savent qu'il a été le premier à réaliser que la mécanique quantique conduisait au phénomène de la création de particules en cosmologie relativiste, bien avant les travaux de Zel'dovich, Starobinsky et Hawking, et qu'il était un concurrent d'EinsteinEinstein dans les années 1940 et 1950, avec des tentatives d'unification des lois relativistes de la gravitation et de l'électromagnétisme.

Schrödinger (on peut l'écouter parler dans une vidéo) se passionnait aussi pour les grandes questions philosophiques comme dans son ouvrage intitulé Qu'est ce que la vie ? qui a tant influencé les fondateurs de la biologie moléculairebiologie moléculaire et les découvreurs de l'ADN. Max Tegmark lui emboîte d'ailleurs le pas en proposant une théorie de la conscience en mécanique quantique. Tout comme Schrödinger avait d'emblée éliminé toute interprétation vitaliste, comme celle de l'élanélan vital de Bergson, en postulant une identité absolue des lois qui président à la mise en forme de la matièrematière, qu'elle soit inerte ou vivante, Tegmark fait de même pour la théorie de la conscience qu'il expose dans son livre Notre univers mathématique. Nous y reviendrons dans son interview.

L'un des pères de la mécanique quantique, le prix Nobel de physique Erwin Schrödinger. Sa mécanique des ondes de matière gouvernées par l'équation portant son nom a permis de comprendre les propriétés des atomes et des molécules. © Cern

L'équation de Schrödinger et la cosmologie quantique

Il se trouve que dans le cadre de l'interprétation de la mécanique quantique dite de Copenhague, l'observation se trouve dotée d'un statut particulier. On pourrait dire qu'elle interdit de parler de l'existence de l'ordinateurordinateur sur lequel vous lisez ces mots en l'absence d'observateurs pour constater sa présence dans la pièce où il se trouve. Certains ont même été beaucoup plus loin en introduisant l'idée que la conscience intervenait directement dans l'existence même et les caractéristiques d'un objet physiquephysique observé.

Schrödinger, tout comme Einstein, était particulièrement insatisfait de cette interprétation ainsi que des probabilités qu'elle introduisait dans la mesure d'un système physique. Il a montré que les bizarreries de la mécanique quantique ne pouvaient pas être confinées au monde des atomesatomes et que l'on devait les retrouver dans la vie de tous les jours, ce que l'on connaît aujourd'hui sous le nom du paradoxe du chat de Schrödingerchat de Schrödinger.

On sait en partie le résoudre avec la théorie de la décohérence mais le problème lié à ce que l'on appelle la théorie de la mesure en mécanique quantique persiste et il devient particulièrement troublant dans les questions de cosmologie quantique.

Pour le comprendre, quelques notions de mécanique quantique sont indispensables. Considérons une pièce dans un jeu de pile ou face. Une description quantique de ce jeu fait mathématiquement intervenir un plan avec deux axes perpendiculaires dont l'un représente l'état pile de la pièce et l'autre l'état face. Imaginons un cercle de rayon unité dont le centre O coïncide avec l'intersection des deux axes. L'équation de Schrödingeréquation de Schrödinger décrit l'évolution dans le temps d'une flèche (que l'on peut appeler l'amplitude de probabilité pour des raisons qui vont devenir claires un peu plus loin) partant de O et dont l'extrémité se trouve sur le cercle. Elle peut se déplacer selon un mouvementmouvement arbitraire ou rester immobile.

Bryce Seligman DeWitt (1923-2004) était un extraordinaire physicien théoricien surtout connu pour ses travaux de pionnier en gravitation quantique. Ils l'ont conduit à soutenir la théorie des mondes multiples d'Everett pour donner sens à ses travaux en cosmologie quantique. © University of Texas

La théorie des mondes multiples d'Everett

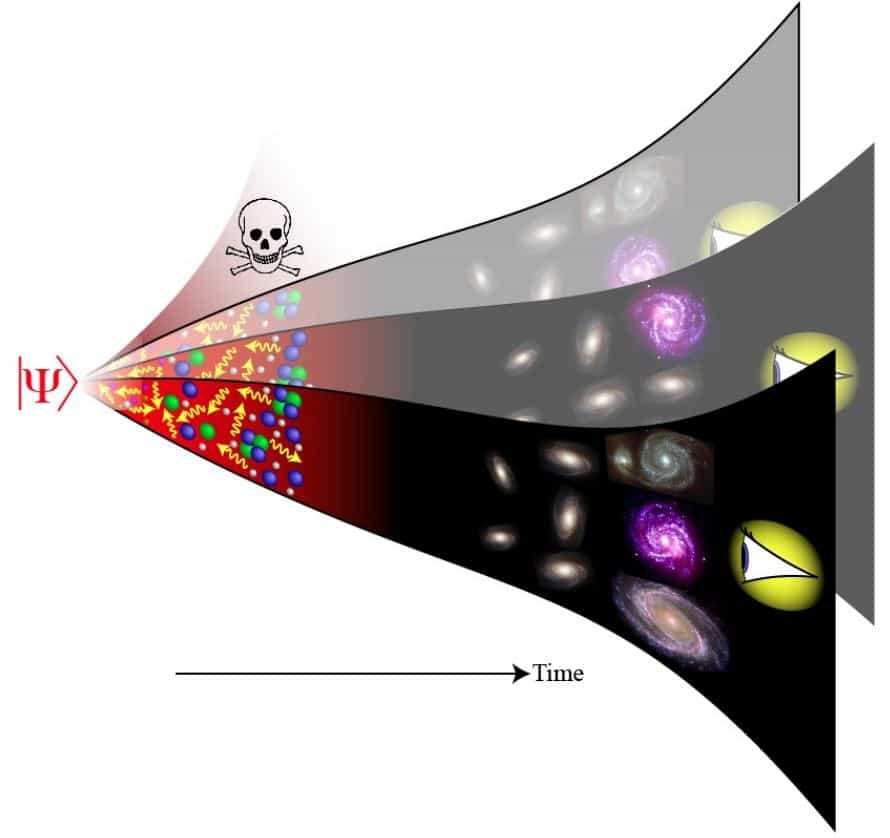
En l'absence d'un observateur, la flèche peut ne pas coïncider avec l'un des axes et la pièce se retrouve dans une superposition d'état à la fois pile ou face, ce qui ne ressemble pas au comportement des pièces que nous connaissons. Elle peut même, on l'a dit, se trouver dans un état fixe dans le temps correspondant à une telle superposition. Mais quand on l'observe, la flèche saute brusquement sur l'un des axes. La probabilité d'observer lors d'une mesure un état pile, ou face, est donnée par le carré de la longueur de la projection de la flèche sur chaque axe. Il y a donc deux lois, celle qui décrit l'évolution de la flèche dans le temps de façon déterministe en l'absence de mesure et celle qui décrit un brusque saut quantique lors d'une mesure et qui ne permet que d'estimer des probabilités d'obtenir une pièce pile ou face.

Cette description est censée être valable pour tous les systèmes quantiques, il suffit de considérer une flèche dans un espace abstrait avec n axes pour n état possibles pour le système, par exemple les 6 faces d'un dé. La première loi s'appelle l'équation de Schrödinger et la seconde le postulatpostulat de la mesure. En considérant l'universunivers en entier vu comme un système quantique, qui contient donc l'observateur et le reste de l'univers, on se retrouve bien gêné puisque son évolution doit alors être décrite par une équation de Schrödinger. Comme, par définition, il n'existe pas d'observateur extérieur à l'univers il pourrait par exemple se retrouver dans un état de superposition entre un mouvement d'expansion et de contraction, sans qu'aucune actualisation dans l'un ou l'autre de ces états ne soit réelle.

C'est parce qu'ils ont été confrontés à ce genre de problème que des théoriciens de la cosmologie quantique, comme John Wheeler et Bryce DeWitt, se sont tournés vers une autre interprétation de la mécanique quantique proposée en 1957 par l'un des élèves de Wheeler, Hugh Everett. On lui a donné le nom de many-worlds interpretation (MWI), soit interprétation des mondes multiples. Selon Everett, il n'y a pas deux lois en mécanique quantique mais une seule.

Pour reprendre l'image du jeu de pile ou face quantique, l'univers évolue de façon déterministe selon l'équation de Schrödinger en se scindant en quelque sorte en deux avec un univers dans lequel la pièce est devenue pile et un autre où elle est devenue face. Il en est de même pour l'observateur qui se scinde en deux copies de lui-même dont chacune n'observe qu'une seule des deux histoires. Les probabilités ne sont que relatives aux copies des observateurs qui se retrouvent clonés dans un ensemble d'univers qui se ramifient selon toutes les histoires possibles associées à des systèmes physiques. La fonction d'onde (c'est-à-dire la solution de l'équation de Schrödinger donnant la probabilité d'obtenir une valeur pour une grandeur physique mesurée) n'effectue en fait jamais de saut quantique. Elle décrit des répartitions de probabilités caractérisant des ensembles d'univers possibles.

Hugh Everett III (1930–1982) a été l'élève d'Eugène Wigner et John Wheeler à Princeton. Son nom reste attaché à une interprétation radicale du formalisme de la théorie quantique éliminant le postulat de la mesure, celle des mondes multiples. © University of California, Irvine

Pendant longtemps, la théorie MWI, pourtant défendue par DeWitt et pendant un temps par Wheeler, n'a pas eu bonne presse. Elle était considérée comme une possibilité assez excentrique et trop radicale pour être prise au sérieux. Mais depuis une dizaine d'années, elle ne cesse de gagner en respectabilité, au point de rivaliser avec l'interprétation de Copenhagueinterprétation de Copenhague et de faire des adeptes. Max Tegmark en fait partie et il a donc appelé multivers de niveau III l'ensemble des univers parallèles, avec des histoires alternatives, qu'introduit la théorie d'Everett.

Remarquablement, on peut se souvenir que c'est Einstein qui fut le premier à introduire le calcul des probabilités en mécanique quantique avec sa théorie des transitions dans l'atome de Bohratome de Bohr. C'est cette théorie qu'Heisenberg a prise pour base pour découvrir sa mécanique matricielle. Einstein n'était donc pas foncièrement opposé à l'usage des probabilités en physique quantiquephysique quantique, contrairement à ce que l'on le dit souvent. Dans une lettre à Pauli, paraphrasant Caton l'Ancien devant le sénat romain, il a clairement formulé sa pensé en disant : « Je ne dis pas probabilitatem esse delendam, mais probabilitatem esse deducendam, ce qui est très différent » (les deux expressions latines peuvent se traduire par il faut éliminer les probabilités et il faut déduire les probabilités).

Que voulait-il dire ? Pour Einstein (qui était sans doute aussi profondément insatisfait du conflit entre les conceptions de l'espace et du temps selon la mécanique quantique et selon sa théorie de la relativité généralerelativité générale), les vraies lois de la physique quantique doivent expliquer pourquoi le calcul des probabilités est nécessaire à la compréhension des orbitalesorbitales atomiques. Il ne voulait par modifier la théorie pour en éliminer (delendam) le caractère probabiliste mais en trouver une plus profonde d'où on pourrait le déduire (deducendam). L'interprétation des mondes multiples offre donc la possibilité d'expliquer d'où proviennent les fameuses amplitudes de probabilité de la mécanique quantique.

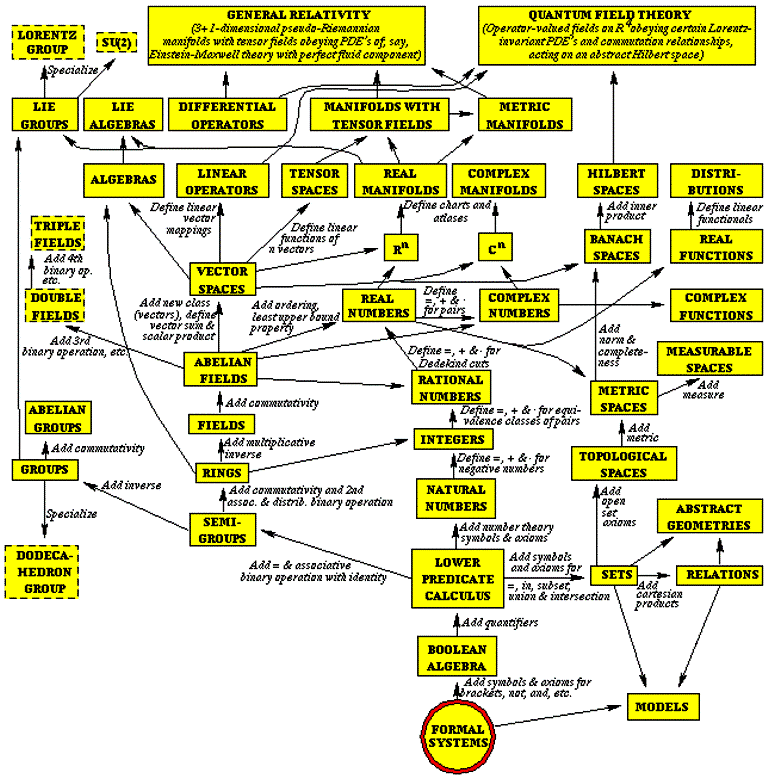
Une carte de l'univers mathématique et de ses multiples emboîtements de structures et embranchements tel que nous le connaissons aujourd'hui. Il contient les deux piliers de la physique théorique, la relativité générale et la théorie quantique des champs (quantum field theory). © Max Tegmark

L'univers mathématique, le multivers ultime

Le multivers de niveau IV est de l'aveu même de Max Tegmark celui qui est le plus spéculatif. Il postule que la totalité de ce qui existe n'est rien d'autre qu'une forme mathématique et qu'inversement, toutes les constructionsconstructions mathématiques possibles sont aussi réelles que notre univers observable. Il en découle que les briques fondamentales de la réalité ne doivent pas être cherchées sous forme de particules élémentairesparticules élémentaires, ou de théorie quantique des champs, mais bien dans le cadre des mathématiques.

Or, des années 1890 aux années 1930 environ, les mathématiciensmathématiciens ont cherché à construire une sorte de théorie fondamentale unifiée de toutes les constructions mathématiques possibles. Les travaux de Cantor, Frege, Russell, Whitehead et Hilbert se signalent particulièrement à cette époque avec les développements modernes du calcul des propositions, des classes et des relations. La théorie des ensembles, où l'on met l'accent sur la notion de structure et de relation, qu'elles soient algébriques ou topologiques, apparaît alors comme le cadre le plus efficace pour unifier et développer LA mathématique comme le montreront notamment les mathématiciens membres du groupe Bourbaki. Ensembles, structures et relations sont donc en quelque sorte les atomes de toutes les constructions mathématiques possibles.

Ces constructions débordent très largement celles des sciences naturelles et même des théories concernant le multivers de niveau II. Comme Max Tegmark identifie ce qui existe à des formes mathématiques, il en découle premièrement que notre univers doit fondamentalement être un ensemble d'éléments ayant des relations et organisés par de multiples structures mathématiques mais que deuxièmement, lui-même n'est qu'une sorte de point dans l'espace des constructions mathématiques possibles toutes aussi réelles que lui. Le multivers IV doit donc aussi contenir les multivers I, II et III.