Les théories actuelles de l'univers jeune comprennent une période d'inflation, juste après le Big Bang, pendant laquelle l'échelle caractéristique de l'univers augmente de 60 ordres de grandeur en moins d'une seconde. Récemment, une équipe internationale comprenant des chercheurs de l'Observatoire de Paris, a proposé d'interpréter les modèles d'inflation en les considérant dans le cadre de la superconductivité, des phénomènes critiques et des transitions de phase. Dans cette nouvelle approche, la forme précise du potentiel de l'inflation est construite à partir des données de WMAP, et des prévisions sont faites quant au modèle d'inflation qui ajuste le mieux les données actuelles.

au sommaire

    L'inflation a été proposée il y a plus de 25 ans pour résoudre le problème de la platitude de l'univers et le problème de l'horizon, entre d'autres ; c.-à-d. expliquer pourquoi on observe des régions dans le ciel qui, bien qu'éloignées de beaucoup plus que le trajet de la lumière depuis le Big BangBig Bang (la taille de l'horizon), ont exactement la même température de rayonnement. Ces régions apparemment ne devraient pas être reliées entre elles, et paradoxalement elles sont remarquabelement homogènes. L'inflation suppose qu'elles viennent de la même région causalement reliée, dont la taille a gonflé considérablement.

    Quel est le phénomène à l'origine de l'inflation ? La Théorie de Grande d'Unification (GUT) donne une explication. GUT unifie l'interaction forte avec l'interaction faible et électromagnétique. Cette unification devrait se produire aux températures de TT = 1029K, seulement disponibles très tôt dans l'univers. Au-dessus et autour de cette température, les particules sont soumises seulement à la force unifiée, et quand l'univers se refroidit au-dessous de cette température, la symétrie entre les forces est brisée, produisant une transition de phasetransition de phase, qui libère une énergieénergie colossale. Cette énergie formidable serait le moteur de l'inflation.

    L'inflation fournit un mécanisme générique pour produire des perturbations scalaires (densité) et tensorielles (ondes gravitationnellesondes gravitationnelles). Un aspect caractéristique des perturbations dûes à l'inflation est qu'elles proviennent de fluctuations quantiques. Lorsque leur longueur d'ondelongueur d'onde devient plus grande que le rayon de HubbleHubble (l'horizon), ces fluctuations sont amplifiées et se développent, devenant classiques et se découplant des processus microphysiques causaux. Ensuite, pendant l'ère actuelle où la matièrematière domine le rayonnement, l'horizon les rattrape à nouveau, et ces perturbations classiques sont la cause des inhomogénéités qui produisent les structures cosmologiques par effondrementeffondrement gravitationnel. L'inflation prévoit de façon générique un spectrespectre de fluctuations primordiales quasi-adiabatiquesadiabatiques (scalaire et tensoriel) gaussien et presque invariantinvariant d'échelle. Ce spectre est parfaitement compatible avec les données riches et précises fournies par la sonde Wilkinson Microwave Anisotropy Probe (WMAPWMAP).

    L'inflation simple est décrite par un champ scalaire (l'inflatoninflaton) qui conduit la dynamique du facteur d'échelle de l'univers, plus de petites fluctuations quantiques. Dans les données de WMAP, les départs à l'invariance d'échelle et à la gaussianité sont déterminés par les départs à la platitude du potentiel, qui peut être mesurée par ses dérivées. Ces dérivées peuvent être combinées dans une hiérarchie de paramètres sans dimension variant lentement.

    Prédictions pour r (le rapport entre perturbations scalaires et tensorielles) en fonction de l'index du spectre scalaire n<sub>s</sub> pour différentes valeurs de l'asymétrie |h| du potentiel. Une valeur maximum de n<sub>s</sub> est trouvée: n<sub>s</sub>max = 0.961528 et la valeur correspondante r est r max = 0.114769. La valeur maximale de r est r absolute-max = 0.16 et correspond à un potentiel purement quadratique. Pour n<sub>s</sub> = 0.95 (valeur centrale observée), 0.03 < r < 0.04 .

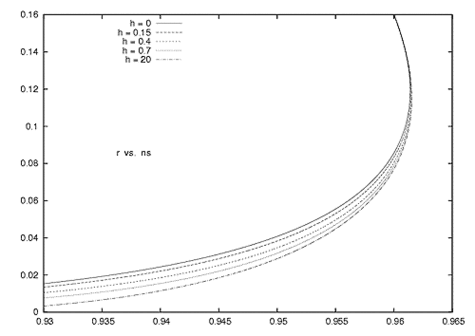
    Prédictions pour r (le rapport entre perturbations scalaires et tensorielles) en fonction de l'index du spectre scalaire ns pour différentes valeurs de l'asymétrie |h| du potentiel. Une valeur maximum de ns est trouvée: nsmax = 0.961528 et la valeur correspondante r est r max = 0.114769. La valeur maximale de r est r absolute-max = 0.16 et correspond à un potentiel purement quadratique. Pour ns = 0.95 (valeur centrale observée), 0.03

    L'équipe propose un modèle simple et réaliste pour étudier l'inflation de base, un potentiel en forme de polynômepolynôme. Dans tous les cas, une formule est trouvée, reliant la massemasse m de l'inflaton aux observables du fond cosmique de rayonnement micro-onde (CMBCMB) : ces observables du CMB sont le rapport des perturbations scalaires et tensorielles, r, et l'index spectral ns des perturbations scalaires. Pour un spectre de fluctuations avec l'index ns s, r.

    Ceci permet de mettre des contraintes sur les modèles d'inflation selon les données actuelles du CMB + LSS (Large Scale Structures). En particulier : (i) Le modèle qui ajuste le mieux les données est le potentiel trinôme avec une limite de masse négative et une petite amplitude initiale d'inflaton. (ii) Pour la valeur centrale ns = 0.95, les valeurs prévues pour r et dérivée de ns sont : 0.03s/d ln k smax = 0.961528 est trouvée, et une valeur maximum correspondante pour le rapport r : rmax = 0.114769. De façon surprenante, le rapport r a deux branches: c'est-à-dire, r est une fonction à deux valeurs de l'index spectral ns dans l'intervalle observable intéressant 0.96s