Un nouveau modèle de Big Bang cyclique récemment proposé éliminait des difficultés avec l'entropie du cosmos observable et permettait de penser un Univers sans début et sans fin dans le temps. Mais, en utilisant des concepts déjà mobilisés par Roger Penrose et Stephen Hawking, même si on peut maintenir la solution qu'il donne à l'énigme de l'entropie du Big Bang, deux cosmologistes pensent avoir montré que ce modèle doit tout de même avoir un début dans le temps même si son futur est infini.
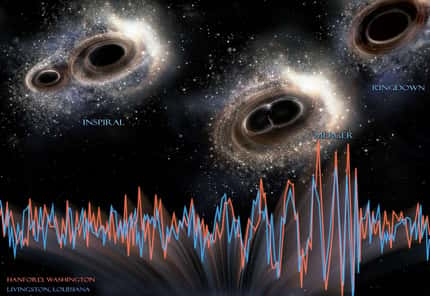
En 1965, le prix Nobel de physique Roger Penrose a publié un théorème démontrant que les équations de la théorie de la relativité générale d'EinsteinEinstein impliquaient que l'effondrementeffondrement gravitationnel d'une étoile suffisamment massive devait nécessairement conduire à une singularité de l'espace-tempsespace-temps entourée d'un horizon des événementshorizon des événements et donc à l'intérieur d'un trou noirtrou noir. Avant lui, on pensait que cette occurrence était un artefact de solutions idéalisées des équations d'Einstein. En 1969, il publiait avec Stephen HawkingStephen Hawking une version améliorée d’un théorème produit par ce dernier qui avait appliqué les méthodes mathématiques et les idées de Penrose à la cosmologie relativiste pour démontrer l'occurrence du même phénomène avec le Big Bang. On pouvait en effet considérer que bien des solutions des équations d'Einstein décrivant un UniversUnivers en expansion étaient plus ou moins équivalentes, en renversant le sens de l'écoulement du temps, à celle décrivant une étoile en effondrement gravitationnel.
Sous des conditions très générales, les équations d'Einstein impliquaient donc que l'espace et le temps avaient un début, début pendant lequel la densité et la température de son contenu, ainsi que la courbure de l'espace-temps, tendaient vers l'infini au fur et à mesure que l'on se rapprochait asymptotiquement d'un instant zéro.
Le prix Nobel Roger Penrose expliquant ses travaux en 2021. Pour obtenir une traduction en français assez fidèle, cliquez sur le rectangle blanc en bas à droite. Les sous-titres en anglais devraient alors apparaître. Cliquez ensuite sur l'écrou à droite du rectangle, puis sur « Sous-titres » et enfin sur « Traduire automatiquement ». Choisissez « Français ». © Tencent WE Summit
Mais déjà, dans l'esprit de Hawking et de ses collègues à cette époque, cela ne devait être qu'un artefact d'un traitement non quantique de l'espace-temps et peut-être aussi tout simplement des équations d'Einstein. Il est en effet possible de considérer des équations différentes gouvernant un espace-temps courbe et lorsqu'un volumevolume du cosmoscosmos observable était beaucoup plus petit au début de l'expansion, son contenu devait se comporter comme un atomeatome quantique. Or, on sait bien que les lois de la mécanique quantiquemécanique quantique assurent justement une taille finie à un atome en supprimant tout effondrement de ses couches d'électronsélectrons sur son noyau. De fait, dès la fin des années 1960, Bryce DeWitt avait posé les fondements d’une théorie quantique de la gravitation applicable en cosmologie.
Les travaux de cosmologiecosmologie quantique qui allaient suivre, par exemple ceux de Stephen Hawking et plus récemment de Carlo Rovelli, allaient revisiter des questions déjà abordées dans les années 1920 et 1930 par Alexandre Friedmann, Georges LemaîtreGeorges Lemaître et Richard Tolman pour l'essentiel.
Entre les mains de ces hommes, il était devenu clair que les équations d'Einstein contenaient des modèles d'univers dans lesquels l'expansion de l'espace finissait par se ralentir avant de s'inverser, ramenant son contenu à une densité infinie. Une nouvelle phase d'expansion pouvait alors débuter et on pouvait donc considérer que la nature avait peut-être « choisi » de se manifester sous forme d'une cosmologie cyclique sans début ni fin, oscillant perpétuellement entre un Big BangBig Bang et un Big CrunchBig Crunch - pour reprendre une terminologie qui n'apparaîtra qu'après la Seconde Guerre mondiale et qui est aujourd'hui bien connue du grand public.
La thermodynamique du Big Bang
Mais, dès les années 1930, l'États-unien Richard Tolman, qui avait commencé sa carrière en chimiechimie physique avant de devenir une sommité mondiale en mécanique statistique, qu'elle soit classique ou quantique, et en relativité, avait posé les bases de réflexions qui allaient montrer qu'il y avait potentiellement un problème avec la thermodynamiquethermodynamique de la cosmologie cyclique relativiste. Un problème qui allait s'aggraver après la découverte du rayonnement fossilerayonnement fossile en 1965.

En effet, Tolman avait donc réussi à transposer dans le cadre des espaces-temps courbes de la cosmologie relativiste les lois de la thermodynamique et en particulier celles reliées étroitement à l'entropieentropie, l'une des fonctions d'état les plus fondamentales de la thermodynamique. Il en résulta finalement par la suite qu'à chaque nouvelle phase d'une cosmologie cyclique, l'entropie de son contenu en matièrematière et rayonnement devait croître (on peut l'estimer avec la mesure du rapport du nombre de photonsphotons au nombre de baryonsbaryons dans le cosmos observable ainsi qu'avec son contenu en trous noirs). C'était difficile à réconcilier avec la constatation que l'entropie mesurée aujourd'hui est non seulement finie mais très loin d'être maximale, si l'on croit qu'il y a aussi bien un nombre infini de cycles dans le passé que dans le futur, comme l'explique le prix Nobel Steven Weinberg à la fin de son fameux livre Les trois premières minutes de l'univers.
La question de ce qui se passe avec l'entropie pour des univers cycliques et de ce qu'en pensait Tolman est plus complexe que ce que l'on vient d'expliquer, mais on continue à réfléchir aux difficultés qu'elle soulève. Il y a quelques années, le célèbre cosmologiste et physicienphysicien théoricien Paul Steinhardt a revisité ces questions avec sa collègue Anna Ijjas.
Les deux chercheurs ont publié des articles sur arXiv faisant intervenir un champ scalaire, comme celui du boson de Higgs, et des équations gouvernant une interaction entre ce champ et l'expansion du cosmos observable. Ce champ scalaire, parfois dit de quintessence, peut servir à décrire la nature de l’énergie noire et il autorise l'accélération de l'expansion du cosmos à se changer en décélération avec contraction.
En soi, ce n'est pas nouveau, mais dans les scénarios similaires étudiés jusqu'à présent suivis d'une phase de rebond, un Big Bounce comme on dit en anglais, la phase de contraction conduisait à la densité de PlanckPlanck et, peu avant de l'atteindre, à une fusionfusion des trous noirs formés pendant la phase. Cette fusion pourrait rendre impossible le rebond et surtout, le passage par une phase quantique devrait faire débuter la phase suivante par un état très élevé de l'entropie du cosmos observable, ce que l'on n'observe pas.
Anna Ijjas explique son travail avec Paul J. Steinhardt sur une cosmologie cyclique. Pour obtenir une traduction en français assez fidèle, cliquez sur le rectangle blanc en bas à droite. Les sous-titres en anglais devraient alors apparaître. Cliquez ensuite sur l'écrou à droite du rectangle, puis sur « Sous-titres » et enfin sur « Traduire automatiquement ». Choisissez « Français ». © Dr Brian Keating
Une cosmologie cyclique sans rebond quantique
Anna Ijjas et Paul J. Steinhardt ont alors montré qu'avec le modèle de champ scalaire qu'ils ont introduit, la contraction s'arrête bien avant d'arriver à la densité de Planck et le cosmos rebondit. Mais il rebondit avec un facteur d'expansion plus grand que lors de la précédente phase, alors que ce facteur est oscillant périodiquement en reprenant ses valeurs dans les précédents modèles de cosmologie cyclique.
Ce faisant, l'entropie supplémentaire produite par la phase précédente est en quelque sorte diluée et repoussée en dehors de ce que l'on appelle l'horizon cosmologiquehorizon cosmologique. Pour un observateur sous cet horizon, il n'y a plus une augmentation continuelle à chaque phase de l'expansion du cosmos observable et il n'y a plus de contradiction entre l'entropie mesurée et un Univers déjà infiniment vieux avec un nombre infini de cycles dans le passé.
Mais, deux autres cosmologistes de l'université de Buffalo aux États-Unis, William Kinney et Nina K. Stein, viennent de jeter un pavé dans la mare. Selon eux, comme ils l'expliquent dans une publication en accès libre sur arXiv, même l'univers cyclique de Ijjas et Steinhardt doit avoir un début dans le temps avec une singularité initiale.
Les deux chercheurs ont repris les raisonnements déjà avancés il y a plusieurs années par Arvind Borde, Alan H. Guth et Alexander Vilenkin, inspirés par ceux de Penrose et Hawking, qui montraient que même la fameuse théorie de l'inflation qui était aussi censée permettre d'éviter une singularité initiale et d'éviter de se poser des questions sur le concept de début de l'Univers, ne pouvait en fait pas faire l'économie de ces deux idées.
Techniquement, il s'agit de la démonstration d'un théorème portant sur ce que l'on appelle la complétude des géodésiques d'un espace-temps. Ces géodésiques sont les trajectoires que doivent prendre des rayons lumineux et des particules de matière sous l'effet seul de la courbure de l'espace-temps. William Kinney et Nina K. Stein, tout comme Arvind Borde, Alan H. Guth et Alexander Vilenkin sont arrivés à la conclusion que des géodésiques dans la cosmologie de Ijjas et Steinhardt ne pouvaient pas être paramétrisées par une variable pouvant atteindre l'infini, ce qui montrait dans le jargon de la géométrie différentielle que ces géodésiques sont incomplètes dans le passé.

C'est pourquoi dans un communiqué de l'université de Buffalo, Kinney explique que : « Les gens ont proposé des univers rebondissants pour rendre l'Univers infini dans le passé, mais ce que nous montrons, c'est que l'un des types les plus récents de ces modèles ne fonctionne pas. Dans ce nouveau type de modèle, qui traite des problèmes d'entropie, même si l'univers a des cycles, il doit encore avoir un début. »
Tout en précisant que : « Malheureusement, on sait depuis près de 100 ans que ces modèles cycliques ne fonctionnent pas car le désordre, ou l'entropie, s'accumule dans l'Univers au fil du temps, de sorte que chaque cycle est différent du précédent. Ce n'est pas vraiment cyclique. Un modèle cyclique récent contourne ce problème d'accumulation d'entropie en proposant que l'Univers se dilate à chaque cycle, diluant l'entropie. Vous étirez tout pour vous débarrasser des structures cosmiques telles que les trous noirs, qui ramènent l'Univers à son état homogène d'origine avant qu'un autre rebond ne commence.
Mais, pour faire court, nous avons montré qu'en résolvant le problème de l'entropie, vous créez une situation où l'Univers devait avoir un commencement. Notre preuve montre en général que tout modèle cyclique qui supprime l'entropie par expansion doit avoir un début. »
Kinney concède cependant : « Notre preuve ne s'applique pas à un modèle cyclique proposé par Roger Penrose, dans lequel l'Univers se dilate à l'infini à chaque cycle. Nous travaillons sur cette question. »