au sommaire

Viggo Brun
Les nombres premiers
La plupart des nombres peuvent se décomposer en un produit d'entiers plus petits : tel est le cas de 28 = 7 × 4 ou de 703 = 37 × 19 par exemple. Mais dès l'antiquité grecque, il était connu que ce n'est pas le cas pour certains nombres tels que 2, 3, 5, 7, 11, 13, 17... Ces nombres indécomposables ont été baptisés nombres premiers, au sens d'élémentaires. Car les nombres premiers permettent en effet de reconstruire n'importe quel entier par multiplication : c'est un théorème important, démontré par Gauss en 1801 dans ses célèbres Disquisitiones arithmeticae.
Le fait qu'il existe une infinité de nombres premiers figure déjà dans les Éléments d'EuclideEuclide. Bien plus tard, Euler redémontre ce résultat par une voie bien différente : en supposant que les nombres premiers sont en nombre fini, la somme de leurs inverses
devrait par conséquent être finie. Or ce n'est pas le cas. bien que la croissance de la série soit très lente, puisque comparable à celle du logarithme itéré log(log(x)).
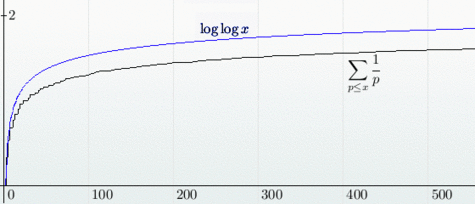
La série des inverses des nombres premiers diverge vers l'infini comme le logarithme itéré log(log(x)).
Crédits : S. Tummarello
Les nombres premiers jumeaux
Les nombres premiers balisent la suite des entiers de manière très irrégulière : tandis qu'il existe de longues plages sans nombre premier1, certains entiers sont immédiatement encadrés par deux nombres premiers, que l'on qualifie alors de jumeaux. Deux nombres premiers sont donc jumeaux si la distance qui les sépare vaut exactement 2, comme pour 3 et 5, ou bien 29 et 31. Les premiers couples jusqu'à 500 sont représentés sur le graphique suivant.
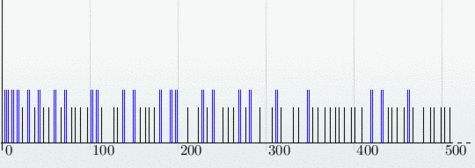
Répartition des nombres premiers : chaque pixel en abscisse représente un entier, une barre verticale indique qu'il est premier, et deux barres verticales bleues qu'il s'agit d'un couple de nombres premiers jumeaux.
Crédits : S. Tummarello
La paire de nombres premiers jumeaux découverte par le projet Twin Prime Search s'écrit 2 003 663 613 × 2195 000±1 et ces deux nombres admettent chacun 58 711 chiffres ! La vérification a été menée à l'aide du test de Lucas-Lehmer et d'un crible préalable (NewPGen). Naturellement, la question est désormais de savoir si ce record peut être battu. Or, bien que les mathématiciensmathématiciens s'accordent à penser depuis environ un siècle qu'il existe une infinité de nombres premiers jumeaux, personne n'est parvenu à ce jour à démontrer cette conjecture malgré de nombreuses tentatives (y compris récemment sur le site arxivarxiv.org).
En particulier, une idée simple consisterait à reprendre le schéma de la démonstration d'Euler : en supposant que la somme des inverses des nombres premiers jumeaux
diverge, les nombres jumeaux ne pourraient être en quantité finie. Toutefois le mathématicien norvégien Viggo Brun a mis fin à cet espoir en prouvant (1919) que cette série est toujours convergente, quand bien même les nombres premiers jumeaux seraient en nombre infini. En son honneur, la somme de cette série s'appelle la constante de Brun et vaut approximativement :
Un projet collaboratif exemplaire
Évidemment l'intérêt de ce nouveau record ne déborde pas pour l'instant du cadre strictement mathématique et, avouons-le, relève pour une large part de l'anecdote. Cependant, il met en exergue le formidable succès du calcul distribué. Le principe en est simple : plutôt que de construire des super-calculateurs trop onéreux, il suffit de tirer profit des ressources non-utilisées des ordinateursordinateurs connectés à InternetInternet. Par suite, et notamment à l'aide de la plate-forme BOINC, chacun peut donc contribuer à la recherche scientifique, simplement en offrant une part de la puissance de calcul de sa machine.
Twin Prime Search (associé à Prime Grid) figure ainsi parmi de nombreux autres projets en cours sur la plate-forme BOINC, qui vont de la détection de signaux extra-terrestres artificiels à l'étude des protéinesprotéines, en passant par la simulation de modèles climatiquesmodèles climatiques. Vous êtes tenté ? Rejoignez l'équipe de Futura-Sciences !
1 Ces plages peuvent être arbitrairement longues, comme il suffit de le constater en considérant la suite n!+2, n!+3, n!+4, ..., n!+n constituée exclusivement de nombres composés (non premiers). Note : n! est la factorielle de n.