au sommaire

Kazimierz Kuratowski (1896 - 1980).
Eau, gaz, électricité... et graphes !
Une énigme bien connue (en tout cas des habitués des forums FSG ;) ) est celle des « trois maisons » : comment, sur une feuille de papier, relier trois maisons à trois services (traditionnellement l'eau, le gaz et l'électricité) de sorte que les conduites et câbles ne se coupent pas ?
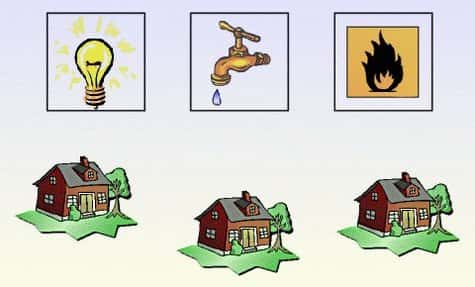
Le problème des trois maisons - trois services : comment alimenter chaque maison en eau, gaz et électricité sans que deux conduites ne se chevauchent ?
Crédits : S. Tummarello
Si vous faites quelques essais au brouillon, vous ne tarderez pas à tomber sur quelques difficultés... Et pour cause : le problème n'admet pas de solution ! En termes mathématiques, on dit que le graphe qui modélise le problème (noté K3,3) n'est pas un graphe planaire. La démonstration réside sur le fait que pour un graphe planaire sans triangle, le double du nombre de sommets est supérieur de quatre au nombre d'arêtes (2s ≥ a+4), ce qui n'est pas le cas de K3,3.
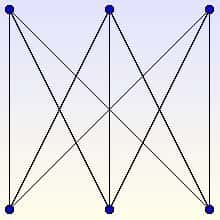
Le graphe K3,3 n'est pas un graphe planaire.
Crédits : S. Tummarello
Dans la même veine, on pourrait se demander comment relier deux à deux 5 villes (données en position générale, i.e. sans alignement) sans utiliser ni pont ni tunnel : il s'agirait donc de savoir si le graphe complet K5 est planaire, les graphes complets (notés Kn où n est le nombre de sommets) étant précisément ceux dont tous les sommets sont reliés deux à deux. Les premiers graphes complets sont illustrés ci-dessous : on peut démontrer sans difficulté que leur nombre d'arêtes vaut n(n-1)2" alt=" " /> où n est le nombre de sommets.
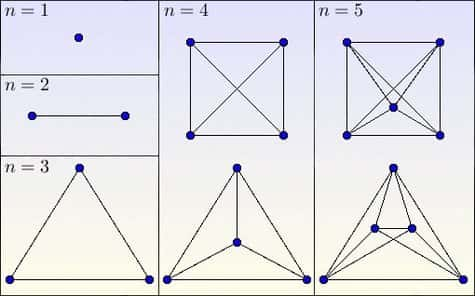
Quelques exemples de graphes complets (n est le nombre de sommets).
Crédits : S. Tummarello
Vous l'aurez compris : de même que pour les trois maisons, un graphe complet admet au moins un croisement dès que le nombre de sommets est supérieur ou égal à 5. Si ces facétieux casse-têtes semblent relever de l'anecdote, les graphes K3,3 et K5 sont pourtant les « prototypes » des graphes non-planaires, ce que le mathématicienmathématicien Kazimierz Kuratowski (1896 - 1980) a démontré en 1930. Les questions deviennent par ailleurs beaucoup plus sérieuses lorsqu'il s'agit d'assembler un grand nombre de composants électroniques sur un circuit imprimé, ou de modéliser des réseaux informatiques ! La théorie des graphes a ainsi toute légitimité à figurer parmi les autres branches des mathématiques, en dépit des critiques qui lui sont parfois adressées.
Le projet Rectilinear Crossing Number
L'équipe de O. Aichholzer s'est intéressé aux graphes complets du plan dont les arêtes sont rectilignes (des segments de droites). Puisque l'on sait qu'au delà de 5 sommets il y au moins un croisement, la question se pose naturellement de déterminer quel est le nombre minimum d'intersections. En 2000, A. Brodsky, S. Durocher et E. Gether de la University of British ColumbiaColumbia (Canada), et indépendamment O. Aichholzer, F. Aurenhammer et H. Krasser. de la Graz University of Technology (Autriche), parviennent à montrer que le graphe complet à 10 sommets admet au moins 62 croisements dans le plan. Si l'équipe de O. Aichholzer renchérit en 2004 en déterminant le nombre d'intersections (102) pour un graphe complet à 11 sommets, la quête de ces « nombres de croisement » en serait restée là sans le calcul distribué.
En effet, la méthode de O. Aichholzer consiste grossièrement à examiner au cas par cas l'ensemble des configurations possibles. Or leur nombre croît exponentiellement avec le nombre de sommets : il y en a déjà 14 millions pour le graphe complet à 10 sommets, et plus de deux millards pour 11 sommets ! Malgré les améliorations apportées à la procédure afin d'éliminer d'emblée une bonne partie des configurations, on comprend que la puissance de calcul du réseau informatiqueréseau informatique universitaire ne pouvait plus suffir. Aussi O. Aichholzer a lancé en 2004 le projet Rectilinear Crossing Number, par lequel chaque internaute peut ainsi mettre à contribution les ressources non-utilisées de son ordinateurordinateur.
18 sommets, 153 arêtes : 1029 croisements
Ce projet s'est avéré très productif car en deux ans, les nombres de croisements ont été calculés pour tous les graphes comprenant jusqu'à n=17 sommets ! Une nouvelle étape vient d'être franchi, en janvier dernier, avec la résolutionrésolution du cas n=18 : les 153 arêtes (rectilignes) d'un graphe complet à 18 sommets se coupent en au moins 1029 points. La figure ci-dessous en montre un exemple où le nombre de croisements est minimum (et donc égal à 1029).
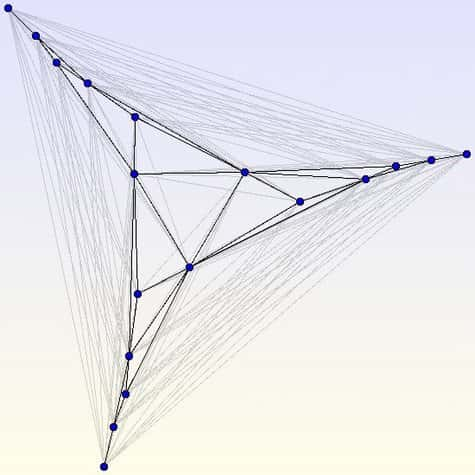
Un graphe complet à 18 sommets comptant exactement 1029 points d'intersection.
Pour plus de clarté, la structure générale du graphe a été mise en valeur.
Crédits : S. Tummarello
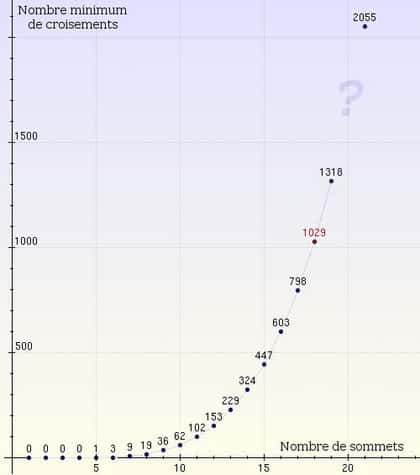
Nombre de croisements en fonction du nombre de sommets : à ce jour, la relation entre les deux n'est pas connue.
Crédits : S. Tummarello
L'équipe de O. Aichholzer prévoit par ailleurs que les nombres de croisements pour n=19 et 21 sont respectivement 1318 et 2055 (la publication est à venir). Néanmoins seuls des encadrements sont connus pour les autres valeurs de n : on sait par exemple que le nombre de croisements est compris entre 1652 et 1657 si n=20. Par conséquent, la prochaine étape sera probablement de mener les calculs pour ce cas, et sûrement d'autres, avant de pouvoir conjecturer une formule générale.
BOINC : La plate-forme de calcul distribué
Le principe du calcul distribué est simple : plutôt que de construire des super-calculateurs trop onéreux en coût et en maintenance, les universités peuvent tirer profit des ressources non-utilisées des ordinateurs connectés à InternetInternet. Chacun peut donc contribuer à la recherche scientifique, simplement en partageant le surplus de puissance de calcul de sa machine. Vous êtes tenté ? Rejoignez l'équipe de Futura-Sciences !