au sommaire

Autoportrait de Léonard de Vinci. © Domaine public
On ne présente plus le génie de la Renaissance qu'était Léonard de VinciLéonard de Vinci. En bon platonicien, celui-ci cherchait des lois mathématiques dans les manifestations de la nature. Mais contrairement à Platon, l'expérience et la pratique de l'ingénieur étaient d'une importance considérable pour Léonard dans ses investigations du monde naturel. Il était donc très moderne en combinant ces deux approches à la base de la croissance de la connaissance scientifique.
On trouve dans les carnets de Léonard de Vinci une fascinante observation que l'on peut traduire par une équation mathématique. Une illustration l'accompagnait (que l'on peut voir ci-dessous) montrant que Léonard avait découvert une loi que l'on relierait aujourd'hui à la géométrie fractale de la nature selon les mots de Benoît Mandelbrot.
Mathématiquement, cette loi dit que lorsqu'une branche se divise une première fois en plusieurs autres branches, le carré du diamètre de cette branche est égal à la somme des carrés des diamètres des branches secondaires. La même loi reste valable pour chacune des branches secondaires. Au final, c'est le carré du diamètre du tronc d'un arbre qui doit être égal à la somme des carrés des diamètres de ses branches terminales.
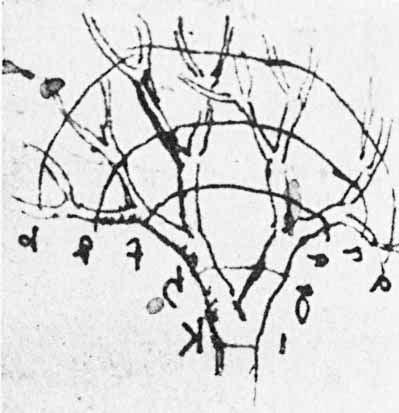
Dessin extrait d'un des carnets de Léonard de Vinci illustrant sa découverte de la loi mathématique gouvernant les diamètres des branches d'un arbre. © Domaine public
Expérimentalement, on sait que la règle de Léonard est presque vraie et qu'elle s'applique à de nombreux arbresarbres. Plus précisément l'exposant des diamètres des branches n'est pas rigoureusement égal à 2 mais varie entre 1,8 et 2,3. Toujours est-il que l'on est bien en présence d'une loi fractale comme on en rencontre souvent dans la nature, par exemple dans les solides quantiques ou le vent solaire.
Mais quelle est l'origine physique de cette loi ?
Comme elle fait intervenir en gros le carré d'un diamètre, c'est-à-dire que l'on peut la relier à une égalité entre des sommes de surfaces des sections des branches, il est tentant de faire intervenir des considérations d'hydrodynamique. La loi biomathématique de Léonard pourrait ainsi simplement exprimer la conservation du flux d'eau, du tronc à la ramure.
Un problème de résistance des matériaux
Comme d'autres avant lui, Christophe Eloy n'est pas satisfait par cette explication et a entrepris d'en trouver une autre. Il vient d'exposer sa théorie dans un article de Phys. Rev. Lett.
Le chercheur s'est attelé à ce problème de biologie théorique en utilisant bien entendu un modèle fractal à la base. Mais cette fois, ce qui est entré en jeu, c'est la physique de la résistancerésistance mécanique des matériaux à une contrainte donnée. Le réseau de branches peut ainsi être considéré comme une série de structures en porteporte-à-faux comme on peut en trouver en architecture. Dans ces cas-là, les ingénieurs du génie civil se posent le problème de la résistance au ventvent.
Christophe Eloy a donc effectué une simulation sur ordinateurordinateur dont le but était de déterminer quelle était la meilleure structure pour des branches capables de résister au vent. Remarquablement, la simulation numériquesimulation numérique reproduit précisément la règle de Léonard de Vinci avec des exposants qui varient entre 1,8 et 2,3.
Nul doute, ce résultat aurait enchanté l'ingénieur et le mathématicienmathématicien qu'était Léonard.