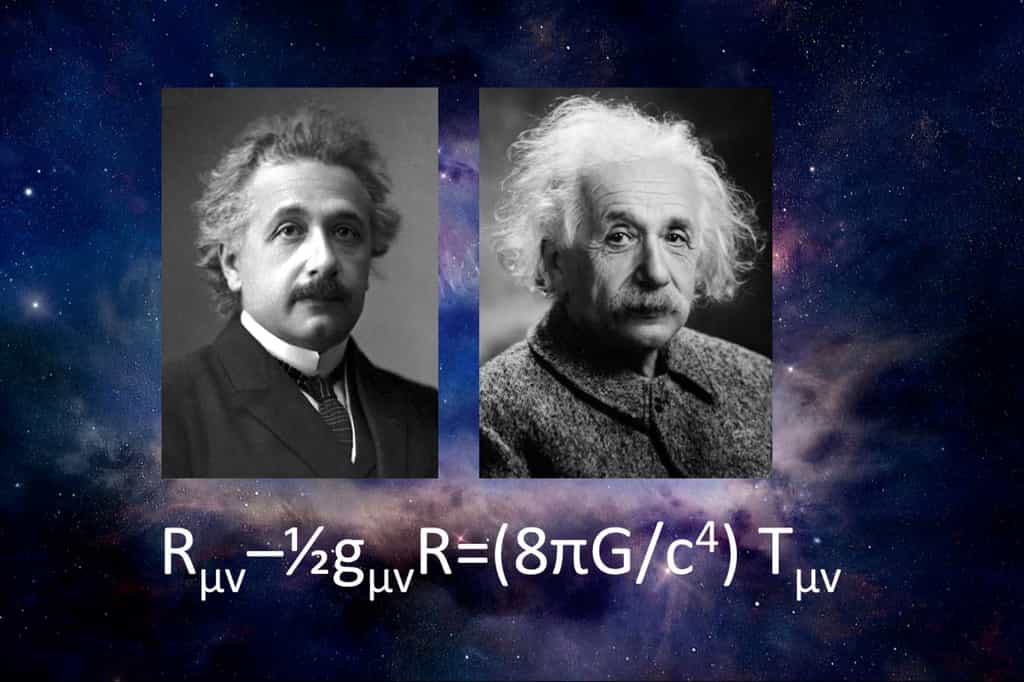La théorie de la relativité intriquée succédera-t-elle à la théorie de la relativité d'Einstein ? (1/2)

On explique souvent qu'EinsteinEinstein a été inspiré par ce qu'il a appelé lui-même le principe de Mach aussi bien pour la découverte de la théorie de la relativité générale que pour la constructionconstruction du premier modèle de cosmologie relativiste en 1917. Dans l'article qu'il publie à ce sujet cette année-là, Einstein introduit dans les équations de sa théorie relativiste de la gravitation une constante, la fameuse constante cosmologique. Il y aurait beaucoup à dire sur les raisons exactes qui ont poussé Einstein à introduire cette constante, notée Λ, dont l'origine peut s'interpréter de diverses manières, mais notamment afin de satisfaire le principe de Mach, tel qu'il l'écrivit par la suite à de Sitter.

Mais de quoi parle le principe de Mach en fait ? Généralement, on l'introduit de la façon qui va suivre, comme peuvent en témoigner certains passages de deux introductions célèbres à la cosmologie relativiste Principles of cosmology and gravitation de Michael Berry, et Introduction to cosmology de Jayant Narlikar.

Il y a environ quatre siècles, pour rendre compte du fait que les expériences sur Terre ne semblaient pas manifester le mouvement de révolution de la Terre autour du Soleil et sans doute aussi à aider à interpréter les mouvements apparentsmouvements apparents des planètes dans le référentielréférentiel lié à la Terre dans le cadre du modèle héliocentriquehéliocentrique de CopernicCopernic, GaliléeGalilée fut conduit à postuler que les lois de la mécanique étaient les mêmes pour tous les observateurs en mouvement pouvant être considérés à une excellente approximation comme rectilignes et uniformes. Les vitessesvitesses étaient donc relatives à un observateur donné et on pouvait formuler simplement le principe d'inertieinertie, fondement de  la mécanique.

Les principes d'inertie et de relativité, des fondements de la physique

Mais, comme NewtonNewton allait le montrer, si la vitesse semble relative selon le principe d'invariance de Galilée pour les lois de la mécanique, l'accélération semblait bel et bien absolue et des expériences de mécanique permettaient de montrer que l'on se trouvait dans un référentiel accéléré, ou pas, et donc de découvrir le mouvement de la Terre même sous un ciel nuageux ne montrant pas les mouvements des étoilesétoiles et du Soleil, ce que Foucault démontrera avec sa fameuse expérience avec un pendule. Newton expliquait aussi que lorsque l'on mettait en rotation un seau d'eau, la force centrifugeforce centrifuge déformant sa surface pour lui donner la forme d'un paraboloïde montrait bien le caractère absolu de l'accélération, accélération qui indiquait l'existence d'un repère absolu à partir duquel on pouvait donner une valeur tout aussi absolue à la force d'accélération centrifuge, à savoir l'espace lui-même.

Ni le mathématicienmathématicien et philosophe allemand Gottfried Leibniz du temps de Newton ni plus tard au cours de la seconde moitié du XIX^e siècle le physicienphysicien et philosophe autrichien Ernst MachErnst Mach ne furent convaincus. Ils trouvaient vide de sens l'idée d'un espace vide absolu car comment pouvait-on vraiment lui rapporter un mouvement, contrairement à ce que fournit un corps matériel, par exemple la surface de la Terre.

Mach ébaucha une solution pour rendre invariante les équations de la mécanique pour tous les référentiels, accélérés ou pas, et rendre donc l'accélération tout aussi relative que la vitesse. Si l'on reprend l'expérience du seau d'eau de Newton, ce qu'il faut bien considérer selon Mach, c'est d'abord que l'eau se trouve en mouvement par rapport aux étoiles à longues distances dans le cosmoscosmos observable et surtout ensuite que ces étoiles exercent une force sur l'eau en cas de mouvement d'une portion de matièrematière s'éloignant de certaines de ses étoiles pour se rapprocher d'autres. L'ensemble des forces exercées en provenance par exemple d'une coquille sphérique d'étoiles attirant dans toutes les directions produirait alors la force d'inertie de cette portion de matière et sa persistance dans un mouvement rectiligne et uniforme en l'absence d'une source de force proche et plus intense, par exemple la Terre. On obtiendrait une explication de l'inertie d'un corps, des particules de matière le composant, c'est-à-dire sa tendance à persister dans un état de repos ou de mouvement rectiligne uniforme en l'absence de forces (à part la somme des forces de gravitationforces de gravitation exercées par les étoiles et autres distributions de matière dans tout le cosmos observable).

Selon Mach, si l'on retirait toutes les étoiles et plus généralement tous les corps matériels à l'exception du seau de Newton en rotation, les forces d'inertie et donc a fortiori la force centrifuge, et même la massemasse de l'eau, disparaîtraient. Il serait donc impossible de mettre en évidence la rotation sur lui-même du seau non seulement par une expérience de mécanique mais aussi parce que nous n'aurions aucun objet pour constater un mouvement, comme par exemple celui des étoiles sur la voûte céleste si nous remplaçons le seau de Newton par la Terre isolée et unique dans l'espace avec nous à sa surface. Une autre façon de présenter l'idée proposée par Mach est de dire qu'en principe aucune expérience ne permet de dire si la Terre tourne par rapport à une coquille d'étoiles, ou de galaxiesgalaxies, fixes absolument, ou si c'est la Terre qui est fixe et la coquille de matière qui est en rotation autour d'elle car dans les deux cas, les forces en présence proviennent de toute la matière dans l'UniversUnivers en ce qui concerne ce que l'on appelle des forces inertielles en relation avec de la matière douée de masse.

Einstein pensait avoir obtenu une forme concrète des idées de Mach via sa théorie de la relativité généralerelativité générale dont certains calculs suggéraient bien que l'inertie entre les corps dépendait de leurs interactions gravitationnelles au sens de la relativité générale. Il alla même jusqu'à déclarer que l'existence de l'espace-tempsespace-temps lui-même était si étroitement liée à celle de la matière que supprimer le contenu matériel de l'Univers devait conduire à la disparition de l'espace-temps. Mais sur ce point, il a dû revoir son opinion lorsque l'astronomeastronome néerlandais Willem de Sitter lui démontra que la théorie de la relativité générale contenait bel et bien des solutions cosmologiques d'Univers... sans  matière !

Jusqu'à la fin de sa vie, Einstein travaillera cependant sur des théories unifiées et non dualistes généralisant sa théorie relativiste de la gravitation. Il s'agissait non seulement de prouver que le champ électromagnétiquechamp électromagnétique était lui aussi une manifestation d'une certaine géométrie de l'espace-temps mais que les particules de matière elles-mêmes devaient être des concentrations d'énergieénergie, et donc de masse selon son équation E=mc², d'un seul et unique champ unitaire englobant la gravitation et l'électromagnétismeélectromagnétisme.

Plusieurs théories relativistes de la gravitation sont possibles

Après sa mort en 1955, les recherches sur le principe de Mach et des théories unitaires de la physiquephysique se sont poursuivies et elles ont conduit à partir des années 1960 à proposer des théories dites tenseurtenseur-scalaires comme celle de Carl Brans et Robert Dicke, appelée théorie de Brans-Dicke et qui peut aussi émerger des théories de Kaluza-Klein, comme l'a montré Pascual Jordan, un des fondateurs de la mécanique quantiquemécanique quantique et pionnier des théories de KK.

Dans le cas de la théorie de Brans-Dicke inspirée par le principe de Mach et les idées du directeur de thèse de Stephen HawkingStephen Hawking, Dennis Sciama (voir les livres de Berry et Narlikar précédemment cités), la constante de la gravitationconstante de la gravitation de Newton dépend du contenu de l'Univers et peut varier dans l'espace et le temps comme le feraient des champs scalaires dont les exemples les plus simples à comprendre sont ceux de la température ou de la pressionpression sur Terre.

Comme la théorie de la gravitation fixe la géométrie de l'espace-temps avec un champ défini là aussi en tout point de l'espace-temps mais sous la forme d'un tenseur, on parle plus généralement des théories de la gravitation cousine de celle de Brans-Dicke comme des théories tenseur-scalaires. On peut les tester en étudiant les mouvements des corps matériels, la trajectoire des rayons lumineux et plus généralement la propagation des ondes électromagnétiquesondes électromagnétiques en espace-temps courbes et aussi avec les ondes gravitationnellesondes gravitationnelles émises par des systèmes binairessystèmes binaires d'astresastres compacts (trous noirstrous noirs ou pulsarspulsars).

Toutes les théories alternatives à la théorie de la gravitation d'Einstein peuvent se formuler en utilisant un cadre très général pour la physique découvert il y a plus de deux siècles par le grand mathématicien Lagrange et reposant sur ce que l'on appelle le principe de moindre action. Appliqué à la physique moderne, il conduit à considérer ce que l'on appelle des lagrangienslagrangiens (voir pour s'en convaincre les cours de physique théorique du grand physicien russe Lev Landau) et c'est ainsi qu'il en existe un pour décrire les équations de la gravitation d'Einstein et un pour décrire les équations des autres champs de la physique décrivant les particules de matière et des autres forces (neutrinosneutrinos, quarksquarks, photonsphotons, gluonsgluons, etc.), y compris le champ du fameux boson de Brout-Englert-Higgs.

Désignons pour faire simple par R, le lagrangien de la théorie d'Einstein (R est relié aux fameux tenseurs de courbure de Riemann qui décrit la courbure de la géométrie d'espace à n dimensions) et L_m, le lagrangien du reste de la physique. Dans le cas du modèle standardmodèle standard de la physique bien établie, le lagrangien total résumant notre connaissance des particules du cosmos observable peut s'écrire en gros sous la forme suivante : R+L_m.

Des alternatives aux équations d'Einstein remplacent R par une fonction f(R) non linéaire pouvant se réduire à R lorsque la courbure de l'espace-temps n'est pas très forte. Ainsi, f(R) pourrait se réduire à aR+bR² par exemple, avec a et b qui sont des constantes fixées par la forme de la fonction f(R). Des théories non linéaires analogues faisant intervenir d'autres termes (tenseur de Ricci, tenseur de Riemann, tenseur métrique, etc.) issues de ce que l'on appelle la géométrie différentielle des espaces courbes existent. Là aussi, dans des conditions peu extrêmes, elles peuvent redonner la théorie d'Einstein avec certaines expressions de f, tout comme celle-ci redonne la physique de Newton avec des faibles densités et des vitesses lentes par rapport à celle de la lumièrelumière.

On a proposé de les utiliser pour rendre compte de la nature de l'énergie noireénergie noire, voire de la matière noirematière noire. Ces théories sont contraintes par des observations dans le Système solaireSystème solaire, les pulsars binaires mais aussi les galaxies manifestant des effets de lentilles gravitationnelleslentilles gravitationnelles notamment.

Malgré tout, bien des possibilités restent ouvertes qu'il reste à exploiter pour construire des alternatives aux équations de la relativité générale, unifier la physique et pour résoudre les problèmes les plus importants de la cosmologie et de la physique fondamentale, par exemple avec l'existence ou non de singularités de l'espace-temps au cœur des trous noirs ou à l'origine du Big BangBig Bang.

Nous voici en possession de quelques clés nécessaires pour aborder dans un second article la théorie de la relativité intriquée.