Une nouvelle expérience de physique quantique jette un nouveau pavé dans la mare de la réalité objective. Afin de ne pas laisser en reste ceux de nos lecteurs qui ne seraient pas familiers avec la physique quantique, nous reprenons tout de zéro, avec des termes simples.
au sommaire
Dans son livre The Character of Physical Law, le physicienphysicien Richard FeynmanRichard Feynman écrit : « Je pense pouvoir affirmer sans risque que personne ne comprend la mécanique quantique. » Si les ressorts de cette discipline encore jeune (à peine un siècle) questionnent profondément les rares esprits qui s'adonnent à son étude, l'on sait néanmoins que la physique quantique décrit avec une précision confondante les comportements les plus contre-intuitifs des atomes et des particules, posant souvent plus de questions qu'elle n'en résout. Bien qu'il ne fasse plus aucun doute que, pour le physicien classique, la mécanique quantique avance parfois à rebours du sens commun, la manière dont elle le fait demeure encore incertaine.
Néanmoins, une récente étude parvient aujourd'hui à apporter de nouveaux éléments de réponse que nous allons ici tenter d'expliquer dans les termes les plus simples et les plus clairs possibles.
« Être et ne pas être », disait le chat de Schrödinger
Pour les chercheurs travaillant en dehors du champ de la physique quantique, le monde possède deux qualités importantes. Il est à la fois :
réaliste, c'est-à-dire que la réalité est objective et ne dépend pas d'une mesure ou d'un observateur ;
déterministe, c'est-à-dire que la réalité n'est pas aléatoire mais le fruit d'un ensemble de variables produisant des résultats systématiques et prédictibles (pourvu que l'on dispose de toutes les informations nécessaires à sa compréhension).
Or, la physique quantique nous apprend qu'il en va bien autrement en deçà d'une certaine échelle, dans le monde exotiqueexotique des atomes et des particules, voire des molécules. Imaginons qu'une particule, un peu comme un interrupteur, admette deux états possibles, que nous baptiserons 1 et 0 pour un maximum de simplicité. Si l'on en croit l'interprétation de Copenhague, tandis qu'un interrupteur ne peut être que dans un seul état à la fois (allumé ou éteint), la particule, elle, se trouve dans ce que l'on appelle une superposition d'états, c'est-à-dire à la fois 1 et 0. Cette superposition ne disparaît que lorsqu'un observateur décide de mesurer son état, causant ainsi un effondrementeffondrement de la fonction d'onde. Cette première idée contredit la possibilité d'une réalité unique et objective pour notre particule, mais les choses ne s'arrêtent pas là.
En effet, toujours d'après la théorie quantique, la particule ne suit pas une logique déterministe mais probabiliste. On ne peut donc pas prédire l'état dans lequel elle sera, mais seulement calculer la probabilité d'obtenir un état ou un autre. Dans notre cas, et toujours par souci de simplicité, nous dirons que notre particule a une chance sur deux d'être dans l'état 1 ou 0.

L'effondrement est dans les yeux de celui qui regarde
Les scientifiques ignorent encore à ce jour par quel mécanisme la particule passe d'une superposition d'états à un état fixe. Certains ont suggéré que la fonction d'onde s'effondre au moment où la mesure est faite, d'autres encore que l'intervention d'un observateur conscient est nécessaire -- cette dernière notion a amené certains à tordre la physique quantique pour lui faire dire que nous pouvions modifier la fabrique de la réalité par la simple force de notre esprit, ce qui, pour autant que nous sachions, est complètement erroné.
Aujourd'hui, les chercheurs travaillant avec des systèmes quantiques complexes savent qu'un simple coup de ventvent peut causer l'effondrement du fragile château de carte qu'est la superposition quantique, susceptible à l'interaction avec les particules présentes dans l'air. La question de ce qui fait la valeur d'une mesure ou d'un observateur demeure donc encore en suspens.
Particules intriquées et messagerie instantanée
Introduisons désormais une nouvelle dose d'exotisme en abordant la notion d'intrication quantiqueintrication quantique. Nous savons d'ores et déjà que lorsque nous mesurons l'état d'une particule quantique, nous avons 50 % de chance de trouver 1 ou 0. En calculant les probabilités pour la mesure de deux particules, nous obtenons donc le tableau suivant :
| Particule 1 | |||
| 0 | 1 | ||
| Particule 2 | 0 | 25% | 25% |
| 1 | 25% | 25% | |
Mais les particules intriquées, elles, partagent une relation particulière. Liées l'une à l'autre (suite à une manipulation volontaire ou, plus rarement, accidentellement), elles forment un tout inséparable où l'état de l'une est dépendant de celui de l'autre. Plus simplement, les deux particules se trouvent chacune dans une superposition d'états (1 et 0) jusqu'à que l'une d'entre elles soit mesurée. Cette mesure cause un effondrement de la fonction d'onde simultané pour la paire, et chacune se fixe alors dans un état opposé, et ce, peu importe la distance qui les sépare. On obtient donc ce tableau :
| Particule 1 | |||
| 0 | 1 | ||
| Particule 2 | 0 | 0% | 50% |
| 1 | 50% | 0% | |
Cela signifie qu'en théorie, si vous placez une particule sur la LuneLune et sa jumelle sur Terre, la mesure de la particule terrienne (donnant par exemple l'état 1) provoquerait l'effondrement de la fonction d'onde de sa jumelle lunaire (qui acquerrait alors l'état 0) au même instant. Ceux qui se souviennent encore de leurs cours de physique protesteront alors en affirmant que cela est impossible car rien, même l'information, ne voyage plus vite que la lumièrelumière (qui met 1,3 seconde à nous parvenir de la Lune). Et à cela nous répondrons... que vous avez parfaitement raison. EinsteinEinstein n'était d'ailleurs pas le plus grand adepte de cette notion, qu'il surnommait la dérangeante (ou effrayante) action à distance.
Quand (Bell) sonne le glas
Dans les années 1960, le physicien John BellJohn Bell décide d'en apprendre plus sur cette communication manifestement instantanée entre les particules intriquées. Il part ainsi de deux principes initiaux, tirés d'une vision classique du monde :
principe de localité : les particules ne peuvent pas s'influencer mutuellement plus vite que la lumière ;
réalismeréalisme : les particules suivent un fonctionnement déterministe (et non probabiliste) que nous peinons simplement à prédire à cause de variables cachées.
Sur la base de ces deux postulatspostulats, Bell calcule l'ensemble des états possibles pour la mesure d'une paire de particules intriquées (dans un contexte un peu plus complexe que celui que nous avons présenté jusqu'ici) et obtient ainsi un seuil de corrélation théorique. Depuis, de nombreux « tests de Bell » ont été effectués dont les résultats ont infailliblement violé le seuil théorique calculé par Bell. Selon lui, une seule conclusion pouvait être tirée de ce constat : l'un de ses postulats de départ était faux. Mais lequel ?
Le paradoxe de Wigner
Faisons à présent une pause de quelques instants pour aborder une nouvelle expérience de pensée, proposée par le physicien Eugène Wigner à l'époque où Bell travaillait sur son théorèmethéorème. Quelque peu agacé par les questions sans réponses posées par la physique quantique, Wigner décide de jeter un pavé supplémentaire dans la mare en exposant le paradoxe suivant.
Imaginons qu'un ami de Wigner se tient assis dans un laboratoire où il s'apprête à mesurer l'état d'une particule. Le physicien, quant à lui, se trouve à l'extérieur du laboratoire et n'a aucun moyen de savoir ce qu'il s'y passe. En appliquant les équationséquations fournies par la mécanique quantique, nous savons que la particule se trouve dans une superposition des deux états (1 et 0) jusqu'à ce que l'ami de Wigner la mesure, causant à ce moment le fameux effondrement de la fonction d'onde. Mais ce n'est pas tout.
Dans notre expérience de pensée, l'ami de Wigner n'est pas le seul à effectuer une mesure. Wigner peut, à son tour, ouvrir la porteporte et demander à son ami quel résultat il a obtenu. Le laboratoire (et son ami à l'intérieur) est donc en quelque sorte contaminé par la particule et se retrouve lui aussi dans une superposition d'états tant que Wigner n'a pas eu sa réponse.
Wigner (le vrai, pas celui du paradoxe) pose alors la question suivante : quand l'effondrement de la fonction d'onde de la particule se produit-il ? au moment où son ami a pris connaissance du résultat ou lorsque ce dernier lui a été transmis ? Pour Wigner, la conscience de son ami suffisait à causer l'effondrement catégorique et définitif de la fonction d'onde, mais avait-il seulement raison ? Qu'en aurait-il été si son ami avait été un ordinateurordinateur ?

Symphonie pour quatre observateurs et deux particules
Venons-en désormais à l'expérience qui nous intéresse aujourd'hui. « Pour notre recherche, nous avons construit une version étendue du paradoxe de l'ami de Wigner, proposée pour la première fois par Časlav Brukner, de l'université de Vienne », écrit Eric Cavalcanti, coauteur de l'étude parue dans la revue Nature Physics. Dans ce nouveau scénario, nous faisons la connaissance d'Alice et Bob (dans le rôle de Wigner), de Charlie et Debbie (dans le rôle de son ami) et d'une paire de particules intriquées (dans le rôle de... la particule).
Charlie et Debbie se trouvent chacun dans leur propre laboratoire : tandis que Charlie a pour mission de mesurer la particule a de la paire intriquée, Debbie se charge de la particule b. (Rappelons que, conformément au principe d'intrication quantique, si Charlie mesure un état de 1, Debbie trouvera forcément 0 de son côté, et vice versa.) À l'extérieur, Alice et Bob (que nous qualifieront de superobservateurs) font chacun rouler un dé à trois faces (I, II, III) :
si le résultat est égal à I : le superobservateur ouvre la porte du laboratoire et demande à son acolyte quel résultat il a obtenu ;
si le résultat est égal à II ou III : le superobservateur laisse la porte fermée et choisit alors de mesurer la particule lui-même, en faisant fi du résultat obtenu par son acolyte.
Les duos suivent cette procédure sans se préoccuper l'un de l'autre et, à la fin de l'expérience, Alice et Bob comparent leurs résultats afin de calculer le taux de corrélation pour l'ensemble des paires de particules. Tout est clair ? Maintenant, abordons brièvement et le plus simplement possible la manière dont les chercheurs s'y sont pris pour tester ce paradoxe expérimentalement.
La parenthèse pratique
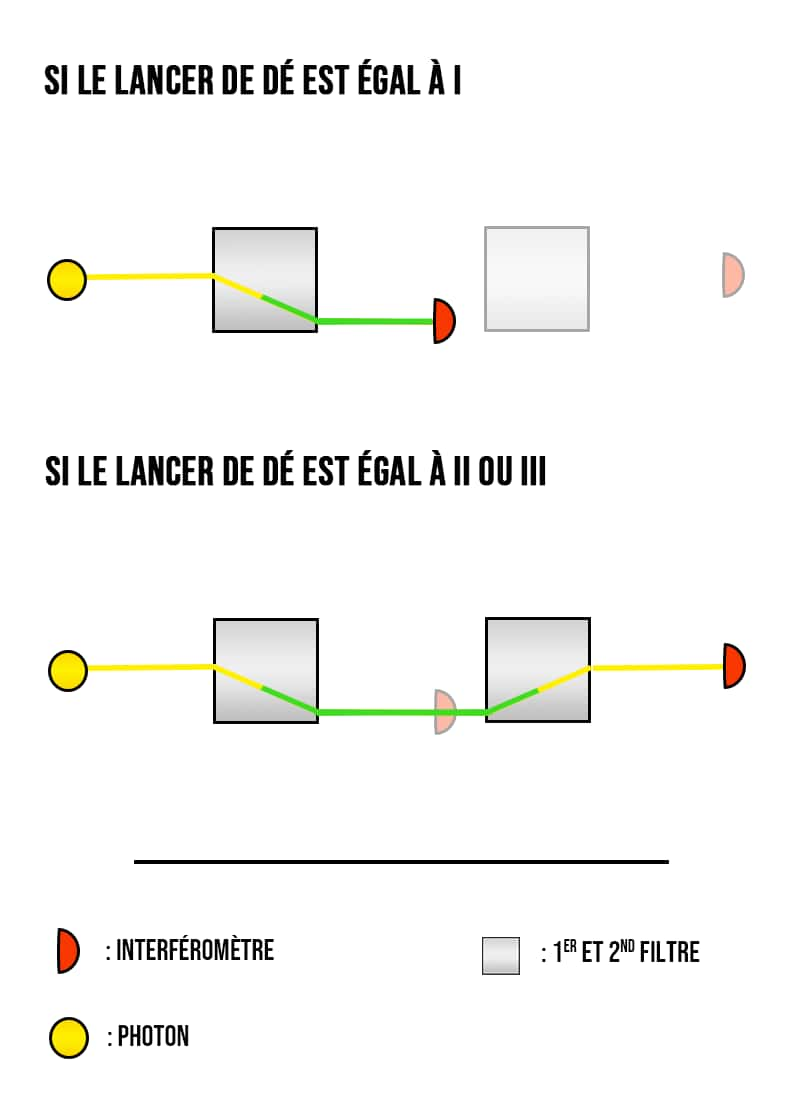
Dans ce contexte plus concret, une paire de photonsphotons polarisés et intriqués est générée et passe par un système complexe de filtres, de prismes, de miroirsmiroirs et de capteurscapteurs. La principale chose à comprendre est que le photon passe d'abord au niveau d'un filtre qui détermine sa trajectoire (par exemple gauche ou droite) en fonction de sa polarisation (1 ou 0). Il a ensuite deux options :
soit il poursuit sa route directement vers un interféromètreinterféromètre qui mesurera son état ;
soit il passe par un deuxième filtre qui annule l'effet du précédent avant que le photon ne parvienne à l'interféromètre.
Ici, le premier filtre désigne l'acolyte, tandis que l'interféromètre prend la place du superobservateur. Dans le premier cas, décrivant la situation où le lancer de dé est égal à I, le résultat obtenu par le filtre/acolyte est directement transmis à l'interféromètre/superobservateur (la porte est ouverte). Dans le second, où le lancer de dé est égal à II ou III, l'observation de l'acolyte est en quelque sorte effacée, et le photon est mesuré directement par le superobservateur (la porte reste fermée). Dans l'expérience, le lancer de dé est généré aléatoirement pour chaque interféromètre, à chaque nouvelle paire de photons.
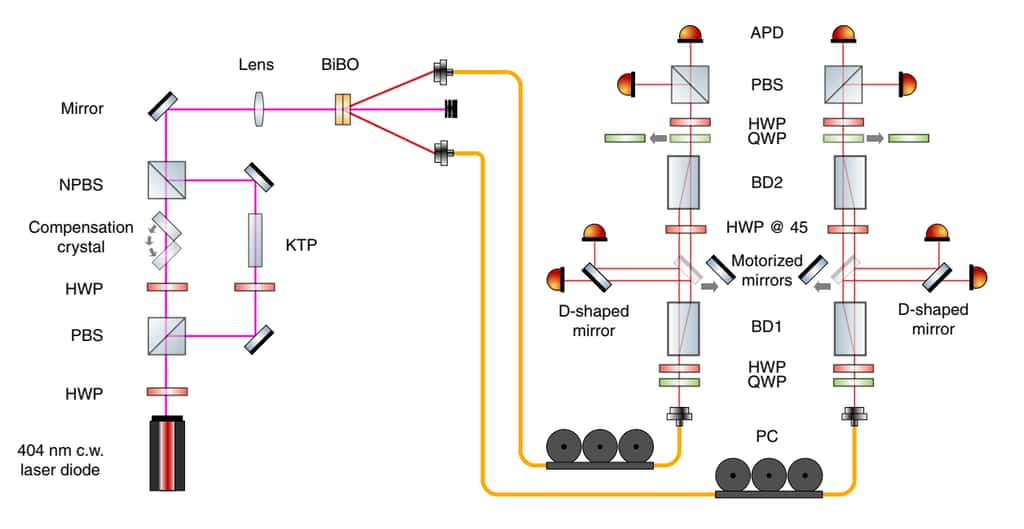
Voici ci-dessous une version très schématique d'une moitié de l'appareil, accompagnée de sa version originale et complète (on vous laisse nous dire laquelle vous préférez).
Trois postulats, avec un twist
Afin de confronter leurs résultats expérimentaux avec les prédictions de la physique classique, les chercheurs établissent leurs calculs théoriques sur trois postulats de base, formant ensemble un principe baptisé « amicabilité locale » par Cavalcanti :
absoluité des événements observés (AOE) : une fois la première observation faite, l'effondrement de la fonction d'onde est absolu est définitif, il n'y a pas de versions alternatives ou de modifications possibles ;
principe de localité : (rappel) les particules ne peuvent pas s'influencer mutuellement plus vite que la lumière ;
absence de superdéterminisme (NSD) : le libre arbitre et l'aléa sont préservés ; le résultat des lancers de dés, par exemple, ne saurait être influencé par un autre événement dans ou en dehors de l'expérience : il est entièrement aléatoire.
Une fois le seuil de corrélation théorique calculé, l'équipe a mené pas moins de 90.000 tests. Comme elle s'y attendait, les corrélations obtenues expérimentalement violent systématiquement les postulats de Bell. Mais, plus intéressant encore, les résultats ne violent le principe d'amicabilité locale (remettant en cause au moins l'un des trois postulats de départ ci-dessus) que lorsque l'intrication est suffisamment forte : en perturbant partiellement l'harmonie des paires de photons, les chercheurs ont constaté qu'au-delà d'un certain seuil, les résultats empiriques rejoignent les prédictions.
Cette distinction permet de démontrer que les postulats de Bell et ceux de l'amicabilité ne sont pas équivalents. Afin d'obtenir des résultats théoriques en accord avec les mesures effectuées dans la réalité, il nous faudra donc abandonner au moins l'un des trois postulats posés par le principe d'amicabilité locale. Et les implications d'une telle découverte sont profondes.
Faudra-t-il mettre à jour notre réalité ?
Comme nous le disions au début de notre article, la mécanique quantique avance parfois à rebours des postulats édictés par le sens commun ; « l'avancée dans ce cas est que nous discernons un peu mieux quels postulats nous devons abandonner », commente Ken Wharton, un physicien de l'université de San José, qui n'a pas pris part à l'étude. En attendant que de nouveaux résultats expérimentaux nous fournissent de plus amples éléments de réponse, les théories continueront de foisonner, certains scientifiques affirmant que les événements futurs peuvent affecter des observations passées (rétrocausalité), que chaque observation provoque la naissance d'universunivers parallèle (hypothèse des multivers), ou encore qu'il n'existe pas de réalité objective. Prochaine étape pour les chercheurs : reproduire l'expérience à des échelles de grandeur supérieure afin de voir jusqu'où la théorie quantique tient bon, et si ses conclusions s'appliquent à notre niveau de perception.
Merci à tous les lecteurs qui auront suivi cet article jusqu'au bout ! Je tiens à aussi remercier humblement Zeeya Merali, pour son article, publié dans Scientific American, qui m'a été d'une grande aide.
Et si la réalité objective n’existait pas ?
Article de Nathalie MayerNathalie Mayer, publié le 19 novembre 2019
Pour la plupart d'entre nous, un fait est un fait. Il peut être prouvé et correspond à une réalité objective unique. Mais le monde de la physique quantique s'apprête une fois de plus à ébranler nos certitudes. Ses lois particulières autoriseraient la coexistence de plusieurs réalités différentes.
« Vous avez droit à votre opinion, mais pas à vos propres faits. » C'est ce qu'avait déclaré à l'occasion d'une conférence de presse en fin d'année dernière, Paul Romer, prix Nobel d’économie 2018 pour ses travaux sur les vertus et les nuisancesnuisances de l'activité économique sur le climatclimat. Mais aujourd'hui, des chercheurs de l'université d'Édimbourg (Écosse) viennent remettre en cause cette affirmation. Selon eux, il existerait plus d'un seul monde objectif. D'un point de vue quantique, tout du moins.
Rappelons au préalable que la méthode scientifique repose par principe sur des observations et sur des mesures reproductibles. Un fait scientifique ne peut ainsi être qu'objectif et accepté par tous les observateurs. Car, dans notre monde, lorsqu'il arrive quelque chose, il arrive indéniablement quelque chose !
“Dans le monde quantique, les observateurs jouissent d’un grand pouvoir”
Rappelons qu'en revanche, dans le monde quantique, les observateurs jouissent d'un grand pouvoir. Il est en effet admis que le simple fait d'observer un système quantique provoque une sorte d'effondrement vers un état spécifique. Ainsi, une particule qui, selon la théorie, peut se trouver dans plusieurs états à la fois -- les chercheurs parlent de superposition -- choisit instantanément son camp dès qu'elle est observée.

Un ordinateur quantique et des photons pour démonter la réalité
En 1961, le physicien Eugène Wigner imagina une expérience de pensée intéressante. Il se demanda ce qu'il adviendrait si un observateur était lui-même observé. Dans une pièce fermée, un ami de Wigner effectue une mesure quantique. À l'extérieur de cette pièce, Wigner n'a pas accès au résultat de la mesure. Il en est réduit à décrire son ami et le système mesuré comme une superposition de tous les états possibles. Car les deux sont enchevêtrés. D'où le paradoxe. La réalité perçue par Wigner et son ami est différente. Pour en donner un exemple « concret », l'ami de Wigner saura si le chat de Schrödingerchat de Schrödinger est mort ou vivant alors que pour Wigner, il restera à la fois mort et vivant.
Cette expérience de l'existence, dans l'univers quantique, de deux réalités objectives, a aujourd'hui pu être testée par les physiciens de l'université d'Édimbourg grâce à un ordinateur quantiqueordinateur quantique constitué de trois paires de photons intriqués. Sur le principe proposé par Caslav Brukner, chercheur à l'université de Vienne (Autriche), de considérer deux couples « Wigner et son ami », les amis en question étant placés dans deux pièces différentes. La première paire de photons tient ainsi la place du système quantique mesuré. La deuxième paire figure les amis de Wigner et la troisième paire, enfin, les deux versions de Wigner lui-même.
Il aura fallu aux physiciens des semaines entières pour collecter suffisamment de données et arriver à la conclusion suivante : l'état du système mesuré par plusieurs observateurs peut être différent et ainsi, la mécanique quantique peut être incompatible avec la notion de faits objectifs. Mais ils soulignent toutefois que cette conclusion repose sur quelques hypothèses qui restent possiblement à valider. Comme le fait qu'un photon puisse être considéré comme un observateur.