Il existe des milliers de nœuds, utilisés dans la marine, la pêchepêche, l'escalade, la constructionconstruction, etc. La plupart des nœuds ont été élaborés de façon empirique et tout bon marin sait par exemple qu'un nœud de cabestan sert à amarrer un bateau ou qu'un nœud de Carrick permet d'assembler deux cordes.

Les modèles mathématiques classiques sont capables de prédire la solidité d'un nœud selon sa structure. Mais ces modèles théoriques ne prennent pas en compte les contraintes mécaniques, comme la force du serrage, le type de corde utilisée, la friction, etc. « Dans la théorie, vous ne vous souciez pas de savoir si vous avez une fibre rigide ou souple, c'est le même nœud du point de vue mathématique », explique Jörn Dunkel, professeur associé de mathématiques au MIT. Ce dernier s'est alors tourné vers son collègue Mathias Kolle, qui avait mis au point en 2018 une fibre spéciale dont la couleur change selon les contraintes de pression.

Grâce à une fibre spéciale dont la couleur change selon les contraintes qui lui sont appliquées, les chercheurs ont défini les paramètres qui rendent un nœud plus ou moins solide. © MIT

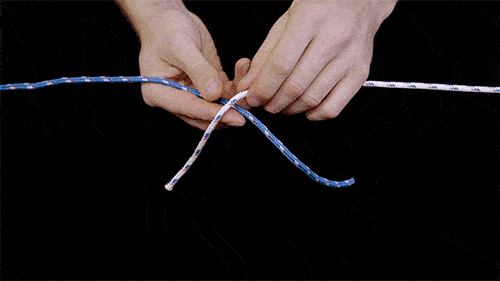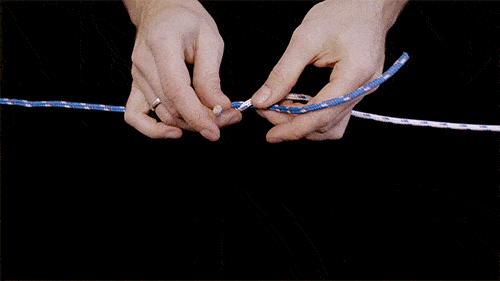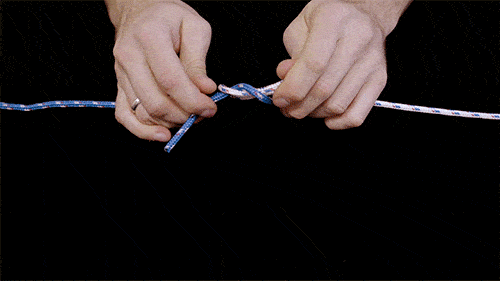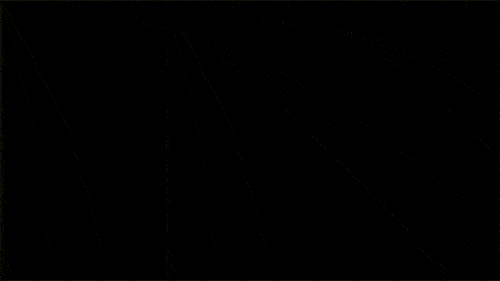
Les deux chercheurs ont noué différents types de nœuds courants utilisés dans la marine ou l’escalade, comme le nœud de huit ou le nœud de trèfle. Ils ont ensuite photographié chaque nœud et noté à quel endroit et quel moment la fibre changeait de couleur, indiquant ainsi la force s'appliquant à la corde.

Ces résultats ont été incorporés aux modèles mathématiques établis préalablement par Jörn Dunkel lorsqu'il étudiait... les spaghettis. Les chercheurs ont constaté que le comportement des nœuds était similaire à celui des spaghettis et ont pu construire un modèle fiable permettant de prédire la solidité d'un nœud.

Les trois grands principes d’un bon nœud

D'après leurs conclusions, décrites dans la revue Science, un bon nœud repose sur trois grands principes :

• un nombre élevé de croisements ;
• des croisements où les brins sortent dans des directions opposées ;
• des brins qui glissent tangentiellement en créant un frottement quand on les tire dans un sens opposé.

« Prenez par exemple le nœud de vachevache et le nœud plat, qui sont presque identiques en apparence. Lorsqu'on tire sur le nœud de vache, il se défait, tandis qu'en tirant les bouts d'un nœud plat, ce dernier va se serrer », explique Vishal Patil, doctorant au MIT et coauteur de l'étude au site NPR. De même, le nœud de Zeppelin est bien plus difficile à défaire que le nœud de vire (aussi appelé nœud de papillon alpin), car il comporte plus de croisements et de torsions.

Le nœud plat est l'un des nœuds les plus utilisés dans la marine, notamment pour fixer les voiles aux vergues. © MIT

Prédire les meilleurs nœuds pour chaque usage

« Nous sommes à présent en mesure d'expliquer pourquoi certains nœuds sont meilleurs que d'autres, se félicite Mathias Kolle. Notre modèle va permettre de décrire quel type de nœud est le plus adapté pour répondre à des contraintes particulières, en médecine (suture), en voile ou en escalade. Et même d'inventer de nouveaux nœuds auxquels que nous n'aurions pas encore imaginé ».

Vishal Patil avoue tout de même être épaté par l'inventivité dont ont fait preuve les humains pour créer autant de nœuds complexes. « J'imagine que quand vous passez un bout de temps en mer, trouver un moyen d'assembler deux cordes est une bonne occupation », présume-t-il.

Physique : le mystère de la solidité des nœuds enfin résolu

Article de Nathalie MayerNathalie Mayer publié le 16/09/2015

Les marins le savent depuis longtemps, à chaque situation correspond un nœud. Mais, qu'est-ce qui fait, au fond, qu'un nœud est plus solidesolide qu'un autre ? Après plusieurs années à se faire des nœuds, des chercheurs viennent enfin de mettre au point un modèle permettant de prédire la solidité d'un nœud.

Tous les vrais marins le savent : le nœud en huit est le plus solide des nœuds d'encordement. Mais, ce que les physiciensphysiciens aimeraient bien comprendre, c'est pourquoi ! La réponse pourrait bien venir des travaux réalisés récemment par Pedro Reis, ingénieur au Massachusetts Institute of Technology (MIT) et par Basile Audoly, expert de la mécanique au CNRS. Ils ont cherché à caractériser les forces qui agissent au cœur des nœuds. Et ils ont trouvé de quoi modéliser, et donc prédire, la solidité des nœuds... ou du moins, la solidité des nœuds simples. Ces nœuds dits d'arrêt qui décrivent une boucle dont les deux extrémités sortent à l'opposé l'une de l'autre.

Optimiser notre façon de nouer nos lacets de chaussures ou comprendre pourquoi les câbles des guirlandes électriques sont toujours emmêlés : ces questions peuvent sembler futiles mais il existe beaucoup d'autres domaines bien plus sérieux dans lesquels peuvent surgir des problèmes de nœuds. La génétiquegénétique en est un exemple. Être capable de calculer la solidité d'un nœud pourrait ainsi aider à comprendre le fonctionnement de processus impliquant les brins d'ADN. Car l'activité biologique de cette étrange moléculemolécule dépend largement de la façon dont elle est enroulée.

C'est peut-être pour ça que les mathématiciensmathématiciens s'intéressent depuis plus de 200 ans à la topologie des nœuds et à la manière dont les brins sont enchevêtrés. L'ennui, c'est qu'ils ne s'étaient encore jamais préoccupés des caractéristiques physiquesphysiques des nœuds. Et c'est en 2008 que Basile Audoly s'est penché pour la première fois sur la question et a établi une théorie permettant de décrire la force qui doit être mise en œuvre pour serrer un nœud simple. Une théorie dont s'est rapidement emparé Pedro Reis. Mais, au cours de ses expériences, menées sur des fils très élastiques en alliagealliage nickelnickel-titanetitane, mauvaise surprise : plus le nombre de boucles augmente, moins la théorie se révèle fidèle à l'observation. En résumé, pour serrer un nœud présentant 10 boucles, une force 1.000 fois supérieure à celle utilisée pour serrer un nœud d'une seule boucle était nécessaire.

Des physiciens du MIT et du CNRS se sont intéressés aux nœuds simples qui décrivent une boucle dont les deux extrémités sortent à l’opposé l’une de l’autre. Selon eux, leur solidité pourrait être prédite à partir de l’épaisseur du fil, de sa rigidité et du nombre de boucles dans le nœud. © Alexander Brock, Wikipedia, CC by-sa 3.0

Topologie du nœud et caractéristiques physiques du fil

En combinant expérimentation et travail théorique, topologie et interactions physiques, les deux chercheurs sont finalement parvenus à modéliser les forces à l'œuvre au cœur des nœuds. Sans grande surprise, ils nous apprennent que la force nécessaire à serrer un nœud dépend de trois variables initialement connues : l'épaisseur du fil, sa rigiditérigidité et le nombre de boucles dans le nœud. Mais le secret de l'efficacité de leur modèle repose sur un postulatpostulat nouveau : le poids des frottements. Car en effet, plus les fils font de boucles, plus les frottements sont importants.

Il aura fallu aux physiciens du MIT et du CNRS, plusieurs itérations entre théorie et expérience avant d'obtenir un modèle fonctionnel. Un modèle auquel on fournit les caractéristiques physiques des fils et la topologie du nœud et qui nous rend, en retour, la force nécessaire à le serrer et, du même coup, une idée fidèle de sa solidité.

Rappelons-le, le modèle des deux physiciens ne prétend pas s'appliquer à tous les types de nœuds mais seulement aux nœuds les plus simples. Ce modèle pourrait toutefois constituer la première pierre d'une théorie décrivant les propriétés physiques de nœuds plus complexes. Jusqu'à maintenant, les problèmes de nœuds étaient généralement abordés de manière empirique. En médecine, par exemple. Mais grâce à cette nouvelle approche, plus rationnelle et prédictive, peut-être les chirurgiens pourront-ils bientôt accorder le nombre de boucles nécessaire avec la solidité attendue de leurs nœuds.