- Consultez notre dossier complet sur la relativité générale

C'est en 1916 qu'Albert EinsteinEinstein a mis un point final à sa fameuse théorie de la relativité générale. Bardée d'équations tensorielles avec des forêts d'indices et faisant usage de la géométrie des espaces courbes à n dimensions, la théorie semblait formidable pour beaucoup. La légende raconte qu'Arthur Eddington, le célèbre astrophysicienastrophysicien ayant apporté la première preuve de la théorie de la relativité générale, se serait vu ainsi apostropher par un de ses collègues : « Eddington, vous devez être l'un des trois hommes sur Terre à comprendre la théorie d'Einstein ». Devant le silence de Sir Arthur, celui-ci ajouta : « Ne soyez pas modeste Eddington », et l'astrophysicien de répliquer : « Au contraire ! Je cherche qui peut bien être ce troisième homme ! ».
Certainement, la phrase attribuée à Sir Arthur n'était pas du tout le reflet de la réalité car dès 1916, plusieurs physiciensphysiciens, astronomesastronomes et mathématiciensmathématiciens ont commencé à publier des travaux importants sur le sujet. Il y eut d'abord Karl Schwarzschild, qui découvre la même année sa célèbre solution contenant en germegerme la théorie des trous noirs, ainsi que l'astronome hollandais Willem De Sitter qui prédit ce que l'on appelle aujourd'hui l'effet Einstein-De Sitter. Quelques années plus tard, Josef Lense et Hans Thirring découvrent que la rotation d'un objet génère un effet particulier sur l'espace-temps environnant.

Hans Thirring en 1925. © Bildarchiv ÖNB, Vienne / AEIOU
De même que le principe d'équivalence implique qu'il n'est pas possible de savoir localement si l'on est au repos dans un champ de gravitationgravitation ou dans un référentielréférentiel accéléré (par exemple à l'intérieur d'une fuséefusée), on ne devrait pas, d'une certaine façon, pouvoir faire de différence entre l'accélération que l'on subit sur un disque en rotation et celle générée par un corps en rotation sur des objets dans un référentiel au repos autour de ce corps. Il en résulte qu'un gyroscopegyroscope en orbiteorbite autour de la Terre en rotation subira des modifications de la direction de son axe initialement pointé vers une étoileétoile, comme s'il était dans un référentiel en rotation.
Des sphères de niobium supraconductrices en orbite
L'effet est minime, presque inobservable, mais il constitue une prédiction intéressante de la théorie de la relativité générale, effet qui peut même être différent selon les théories métriques de la gravitation concurrentes proposées à la place de celle d'Einstein. C'est pourquoi une mission spatiale a été lancée en 2004 pour faire l'expérience : Gravity Probe B (GPB).
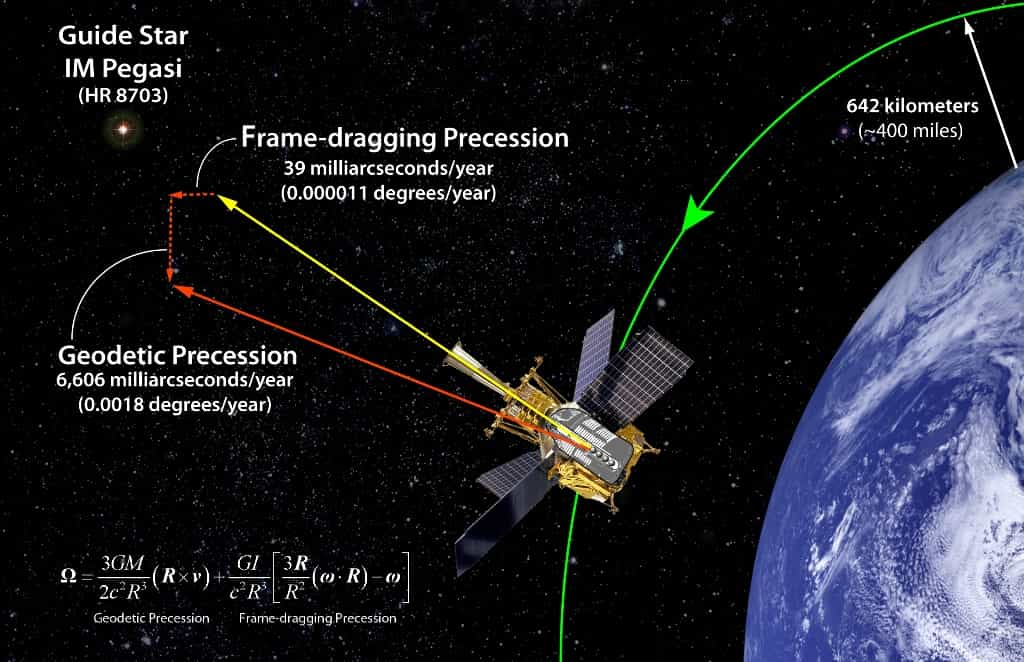
En 2007, les chercheurs annonçaient avoir observé l'effet Einstein de Sitter avec GPB, mais l'objectif principal, la détection de l'effet Lense-Thirringeffet Lense-Thirring, s'est révélé beaucoup plus difficile que prévu à cause de problèmes sur l'instrument de mesure lui-même. La NasaNasa vient cependant d'annoncer, ce 4 mai, que l'obstacle a finalement été surmonté et que l'effet Lense-Thirring, dit encore effet d'entraînement des référentiels (en anglais frame-dragging precession), est bien là, qui plus est conforme aux prédictions de la théorie d'Einstein. Le bilan des mesures, qui devrait bientôt être publié, a été donné.
Les observations montrent (aux erreurs de précision près) une modification de l'orientation de l'axe d'un gyroscope de -6,601 818 3 mas/an par effet Einstein-De Sitter et de -37,272 mas/an (milliseconde d'arc par an) par effet Lense-Thirring alors que relativité générale prévoyait une modification de -6,6061 mas/an et -39,2 mas/an respectivement (rappelons qu'une milliseconde d'arc vaut 4,848 10-9 radianradian).