Des boules mal rangées. Crédit : Roger Smith
En partie pour comprendre la structure de la matière à partir de la théorie atomique mais aussi pour savoir comment stocker le plus grand nombre de boulets de canon dans un volume donné, les mathématiciensmathématiciens et les physiciensphysiciens ont cherché depuis des siècles à déterminer comment empiler des sphères de la façon la plus efficace possible. C'est dans les écrits de Kepler que l'on trouve pour la première fois la conjecture portant son nom et qui ne fut démontrée, selon toute vraisemblance, qu'en 1998 grâce au mathématicien Thomas Hales.
D'après Kepler, l'empilement le plus efficace était celui donnant une structure cubique à face centrée que l'on connaît bien aujourd'hui en théorie des réseaux cristallins. Un tel « pavage » d'un volume par des sphères permet d'occuper environ 74% d'un volume donné.
De telles considérations sont utiles pour expliquer la densité d'un cristal par exemple, et prédire aussi dans quelle mesure on peut y introduire des atomes d'un type différent et occupant un volume sphérique plus petit que ceux ayant initialement servi pour constituer ce cristal. La conception d'alliages avec des propriétés données bénéficie des recherches sur ces questions.
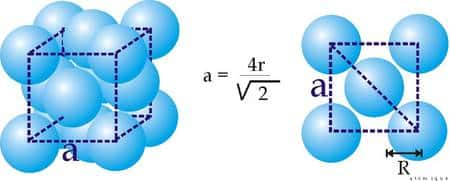
Réseau cubique à faces centrées. Crédit : Université du Québec
Le hasard fait mal les choses
Ces analyses sont pertinentes dans les cas où l'empilement des sphères peut être réalisé de façon parfaite et bien contrôlée. Mais que se passe-t-il lorsque l'on considère, par exemple, des milieux poudreux, comme des avalanchesavalanches de neiges, des cendres volcaniques qui se déposent suite à une nuée ardentenuée ardente, etc., qui sont des phénomènes chaotiques et turbulents ? Peut-on prédire et expliquer la compacité des dépôts observés ?
Le problème est équivalent à celui de considérer des sphères dures secouées dans un cube que l'on cesse ensuite d'agiter. En fonction des forces de frottement existant entre les sphères, quelle est la compacité de l'empilement qui se forme en moyenne ?
C'est à cette question que les physiciens Hernán Makse, Chaoming Song Wang PingPing et du City College de New York ont apporté une réponse possible. Ces trois chercheurs ont modélisé statistiquement ce processus aléatoire. D'après eux, le hasard est bien moins efficace que le vendeur d'oranges qui empile soigneusement ses fruits en suivant les conseils de Kepler. Selon leurs calculs, laissées à elles-mêmes, les sphères ne peuvent emplir plus de 63,5% de l'espace disponible.
Les chercheurs prévoient de mener des expériences pour tester la validité de leur modèle. En particulier, ils ont l'intention de fixer des polymères à la surface de minuscules sphères de silicesilice dans un colloïdecolloïde, de façon à obtenir des forces de frottements données entre les sphères.
Tout cela aurait certainement beaucoup intéressé Pierre-Gilles de Gennes dont on connaissait la passion pour la physiquephysique des milieux granulairesgranulaires que l'on retrouve aussi bien au niveau des dunes de sablesable que dans les poudres utilisées dans l'industrie.