au sommaire
En 1939, Robert Oppenheimer a posé le socle sur lequel les théories des étoiles à neutrons et celle de l'effondrementeffondrement gravitationnel conduisant à la formation d'un trou noir seront construites à la fin des années 1950 et au début des années 1960. Il s'agit des articles écrits en collaboration avec ses étudiants de l'époque : « On Massive Neutron Cores », avec Georges Volkoff, et « On Continued Gravitational Contraction », avec Hartland Snyder.
Avec les progrès de l'astrophysique nucléaire et le renouveau de la relativité générale, entraîné par la découverte des quasars et du rayonnement fossile, le problème de la détermination de l'état final de la matière dans le cas d'une étoile en fin de vie ayant épuisé son carburant nucléaire se posera alors avec plus d'acuité et d'urgence.
Mélangeant relativité générale, thermodynamiquethermodynamique et physiquephysique nucléaire, le plus important ouvrage traitant de ces questions à la fin des années 1960 est probablement celui de Harrison, Thorne, Wakano, et Wheeler : GravitationGravitation Theory and Gravitational Collapse, publié en 1965. Il traite par exemple du problème sur lequel la mesure récente de la massemasse du pulsarpulsar PSR J1614-2230 apporte une nouvelle lumièrelumière : celui de l'équationéquation d'état de la matièreétat de la matière nucléaire à des densités extrêmes.
On sait aujourd'hui que les pulsars sont des étoiles à neutrons en rotation et l'on pense, bien que cela ne soit nullement démontré, que les sursauts gamma courts se produisent à l'occasion de collisions entre deux étoiles à neutrons associées en un système binairesystème binaire. Lors de la collision de telles étoiles, on s'attend aussi à ce que des ondes gravitationnellesondes gravitationnelles soient émises.
Les étoiles à neutrons elles-mêmes sont le résidu de l'effondrement gravitationnel d'une partie de la matière d'une étoile massive explosant en supernovasupernova. Il faut pour cela que sa masse dépasse les 8 à 10 masses solaires. Mais on est loin de tout comprendre du processus et on pense qu'il conduit à la formation d'un trou noir pour des étoiles de quelques dizaines de masses solaires au moins. Il existe donc plusieurs raisons, d'un simple point de vue astrophysique, pour étudier les étoiles à neutrons.
Un laboratoire pour comprendre les forces nucléaires fortes
Surtout, il y a le fait que l'on peut espérer mieux comprendre les forces nucléaires avec ces objets insolites, qui peuvent contenir toute la masse du SoleilSoleil dans une sphère de quelques dizaines de kilomètres de diamètre seulement. En effet, même si l'on comprend assez bien les forces entre les quarksquarks constituant des protonsprotons et neutrons à très haute énergieénergie, les équations de la chromodynamique quantiquechromodynamique quantique (QCD) décrivant ces forces nucléaires fortes deviennent très difficiles à résoudre à plus basse énergie.
Paradoxalement, il est plus facile de déterminer à partir des équations de la QCD les détails d'une collision de deux protons au LHC que d'en dériver les forces entre ces protons et les neutrons au sein d'un noyau. Pire, le simple calcul ab initio de la masse du proton ne peut être fait de façon précise sans l'aide de puissants ordinateursordinateurs.
On peut contourner le problème en étudiant expérimentalement des gazgaz de nucléonsnucléons à haute densité ou température. Les étoiles à neutrons représentent un bon laboratoire pour cette étude. Leurs caractéristiques, comme leurs rayons et leurs masses, vont en effet dépendre de l'état de ce gaz dans leur intérieur.
En quoi le cas de la masse du pulsar PSR J1614-2230 est-il instructif sur toutes ces questions ?
C'est ce que nous avons demandé à Éric Gourgoulhon, directeur de recherche au CNRS et membre du laboratoire UniversUnivers et théories (LUTH), expert en physique des astresastres compacts que sont les naines blanchesnaines blanches, les trous noirs et bien sûr, les étoiles à neutrons.

Éric Gourgoulhon est un expert dans le domaine de l'astrophysique relativiste des astres compacts, comme les étoiles à neutrons et les trous noirs. © LUTH
Futura-Sciences : On trouve parfois dans la littérature une masse limite pour une étoile à neutrons qui est de l'ordre de 0,7 masse solaire. Or, le pulsar PSR J1614-2230 frôle les deux masses solaires, s'agit-il d'un premier conflit entre la théorie et l'expérience ?
Éric Gourgoulhon : Pas vraiment. Cette masse, à laquelle on donne le nom de limite d'Oppenheimer-Volkoff, avait été obtenue en 1939 par ces deux physiciensphysiciens en négligeant les forces que les neutrons pouvaient exercer entre eux. Comme dans le cas de la célèbre masse de Chandrasekharmasse de Chandrasekhar, la masse limite pour une naine blanche, la force de pressionpression qui s'opposait à la contraction gravitationnelle de l'étoile à neutrons provenait de ce qu'on appelle la pression de dégénérescencepression de dégénérescence d'un gaz de particules. Pour une naine blanche, il s'agissait d'un gaz d'électronsélectrons et pour une étoile à neutrons, d'un gaz de neutrons. C'est un effet quantique qui apparaît pour un gaz de fermionsfermions (on parle de gaz de Fermi) et qui trouve son origine dans le principe d'exclusion de Pauliprincipe d'exclusion de Pauli. Mais en fait, cette force de pression est négligeable devant celle résultant de l'interaction nucléaire forte entre les neutrons.
On le savait depuis longtemps. Dès les années 1960, des équations décrivant l'état de la matière nucléaire à forte pression et densité tenant compte des interactions entre les nucléons avaient été proposées. Mais comme ce sont des équations phénoménologiques et bien qu'elles prédisaient des masses supérieures à celle de la limite d'Oppenheimer-Volkoff, il était difficile de donner une valeur limite ferme.
Les observations ont d'ailleurs confirmé qu'il fallait tenir compte de ces forces entre les nucléons dans une étoile à neutrons. En général, celles que l'on observe ont des masses comprises entre 1,3 et 1,5 masse solaire.

De gauche à droite, Robert Oppenheimer, Enrico Fermi et Ernest Orlando Lawrence, l'inventeur du cyclotron utilisé pour sonder le noyau. © Wikipedia, domaine public
FS : Ne peut-on pas reproduire sur Terre les conditions de pression régnant dans une étoile à neutrons, par exemple avec des collisions d'ionsions lourds comme celle que l'on fait au Ganil à Caen ?
Éric Gourgoulhon : Si c'était possible, cela permettrait de lever les ambiguïtés sur l'état des gaz de nucléons dans des conditions extrêmes. Malheureusement, les températures que l'on atteint dans ces collisions sont trop élevées, 1012 K contre 107 K environ. Surtout, la matière nucléaire dans une étoile à neutrons est majoritairement composée... de neutrons, ce qui n'est pas du tout le cas dans les collisions d'ions lourds. On est donc dans une situation inverse, ce sont les observations sur les étoiles à neutrons qui peuvent nous servir à mieux comprendre les forces nucléaires et les paramètres liantsliants pression, température et densité pour l'équation d'état de la matière nucléaire.
En outre, certains des modèles proposés pour l'équation d'état impliquent que le cœur d'une étoile à neutrons n'est pas fait majoritairement de neutrons, comme on pouvait le penser. En plus de ce scénario, on en considère principalement 5 autres. On a ainsi des modèles de cœurs avec :
- un condensat de Bose-Einsteincondensat de Bose-Einstein de mésonsmésons pipi ;
- des kaons, une famille de mésons formés de paires de quarks contenant un (anti) quark étrangequark étrange ;
- des hypérons, une famille de baryonsbaryons formés d'un triplet de quarks légers contenant au moins un (anti) quark étrange ;
- un mélange de quarks légers déconfinés comme dans le plasma de quark-gluongluon ;
- un mélange de quarks légers déconfinés contenant environ 1/3 de quarks upquarks up, 1/3 de quarks downquarks down et 1/3 de quarks étranges. Au lieu d'une sorte de noyau atomique géant riche en neutrons, on aurait alors affaire à un baryon géant. On parle d'ailleurs, dans ce cas, d'étoile étrange.
Selon ces modèles, la masse maximale pour une étoile à neutrons n'est pas la même.

Différents modèles de composition de l'intérieur d'une étoile à neutrons. © Fridolin Weber et Éric Gourgoulhon
FS : Ce n'est pas la première fois que l'on parle d'une masse mesurée pour une étoile à neutrons qui atteint et même dépasse les 2 masses solaires. En quoi l'observation du pulsar PSR J1614-2230 est-elle particulière ?
Éric Gourgoulhon : Elle l'est à cause de la précision de la mesure grâce à l'effet Shapiro et des caractéristiques du système binaire contenant ce pulsar. Beaucoup des étoiles à neutrons dont on peut déterminer la masse ne permettent pas d'obtenir une précision inférieure à 20 %. Dans le cas présent, il y a le fait que l'on est en présence d'un système binaire à éclipseéclipse, l'étoile à neutrons qui tourne autour d'une naine blanche a un plan orbital dont la normale est fortement inclinée par rapport à l'axe d'observation depuis la Terre, 89,17° ±0,02°. Cela rend maximal l'effet Shapiro, lequel nous permet de déterminer précisément la masse de la naine blanche. On peut ensuite déterminer indirectement celle de l'étoile à neutrons comme on le fait dans le cas des systèmes binaires.
Comme l'effet Shapiro croît linéairement avec la masse de l'étoile compagnon du pulsar, on obtient un résultat supérieur de plusieurs ordres de grandeursordres de grandeurs à celui mesuré dans des situations similaires.
De plus, la mesure de masse effectuée ici repose essentiellement sur la relativité générale, ce qui n'est pas le cas des autres mesures de masses reposant sur des modèles astrophysiques. C'est donc un résultat particulièrement robuste.

Quelques-unes des masses des étoiles à neutrons connues en 2004. Remarquez qu'elles sont majoritairement très proches de 1,4 fois la masse du Soleil et que les incertitudes sur ces masses (les intervalles) sont assez grandes. © Éric Gourgoulhon
FS : Qu’est-ce que l’effet Shapiro ?
Éric Gourgoulhon : Il s'agit d'une conséquence des équations de la relativité générale d'Einstein déduite en 1964 par Irwin Shapiro. L'effet est similaire à celui de la déviation des rayons lumineux par un corps céleste comme le Soleil sauf que dans son cas, il se manifeste sous la forme d'un retard dans la propagation des ondes électromagnétiquesondes électromagnétiques, par rapport à une propagation en espace-tempsespace-temps plat. Lorsque la naine blanche éclipse le pulsar, la courbure de l'espace-temps autour d'elle ne permet plus une propagation en ligne droite des impulsions électromagnétiques provenant du pulsar. Les trajectoires de ces impulsions s'incurvent et provoquent un retard d'autant plus important dans le temps de propagation que l'objet responsable de cet effet est plus massif.
Dans le cas de PSR J1614-2230, la forte inclinaison du plan de l'orbiteorbite et la masse élevée de la naine blanche permettent de donner comme estimation de la masse de l'étoile à neutrons 1,97±0,04 M⊙ (masse solaire).
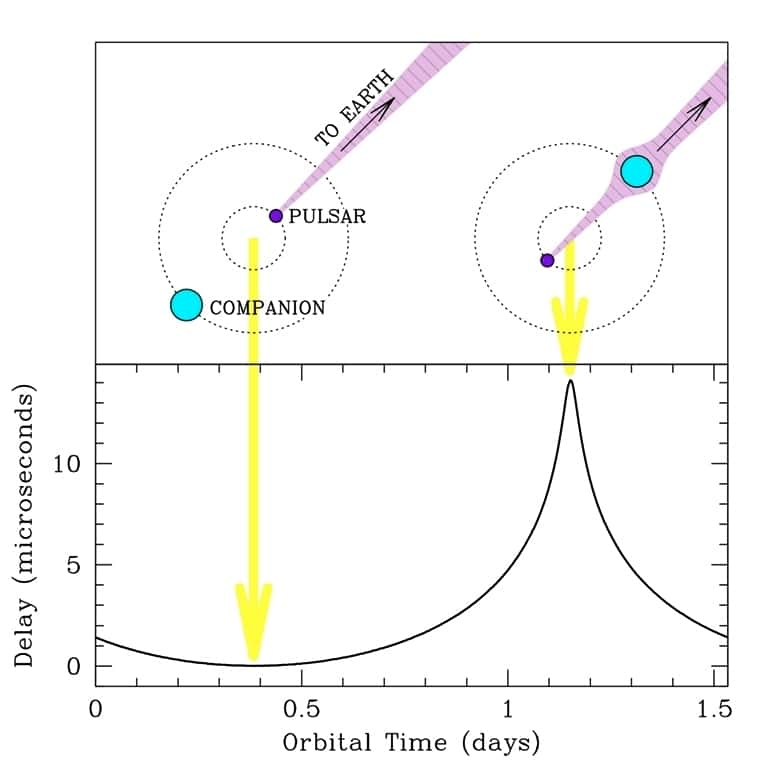
Le principe de l'effet Shapiro pour la détermination de la masse de l'astre compagnon d'un pulsar est illustré sur le schéma du haut. Lorsque se produit une éclipse du pulsar, les ondes radio qu'il émet sous forme d'impulsions n'arrivent plus en ligne droite sur Terre et un retard apparaît. C'est ce que l'on voit sur le graphique en bas avec en abscisse le temps pour la progression des astres en orbite et en ordonnée le retard mesuré sur Terre. © Naval Research Laboratory
FS : Quelles sont les conséquences pour l'équation d'état de la matière nucléaire (et en fait la composition interne du cœur d'une étoile à neutrons) que l'on peut tirer de la précision atteinte pour cette masse et de sa valeur élevée ?
Éric Gourgoulhon : Les modèles avec un cœur d'hypérons, de kaons ou de matière étrange en sortent très défavorisés. J'insiste sur le fait que bien que de nombreuses équations d'états de la matière nucléaire aient été proposées par différents auteurs, reposant sur différents schémas d'approximation de la QCD, il ne peut y avoir qu'une seule équation valable pour toutes les étoiles à neutrons.

Les énergies des masses de systèmes composées de quarks u, d et s (quark étrange). Lorsqu'on a affaire à un système lié, comme l'hypéron lambda en haut à droite, on le signale avec un cercle. En bas, le mélange de quarks libre u,d, s a la plus faible énergie, il est donc thermodynamiquement le plus stable et à priori le plus favorisé pour le cœur d'une étoile à neutrons par rapport aux autres états représentés sur ce schéma. © Éric Gourgoulhon
C'est une conséquence des lois de la thermodynamique et du fait qu'une étoile à neutrons doit représenter l'état d'équilibre final de l'évolution de la matière nucléaire. Les incertitudes sur les modèles de formation de ces étoiles ne doivent pas intervenir. On peut même dire que si une seule étoile à quarks étrange était découverte, toutes les étoiles que l'on appelle actuellement des « étoiles à neutrons » devraient en fait être des étoiles de ce genre, d'autant plus que ce modèle donnait l'état d'énergie final le plus bas et donc à priori le plus favorisé.
On peut encore soutenir des modèles de matière exotiqueexotique mais cela impose des contraintes sévères sur les paramètres de l'équation d'état, dépendants des caractéristiques des forces nucléaires, d'une façon qui n'est pas la plus communément admise. De nombreuses équations d'états, essentiellement parmi les plus exotiques, viennent donc d'être éliminées par cette découverte.