au sommaire
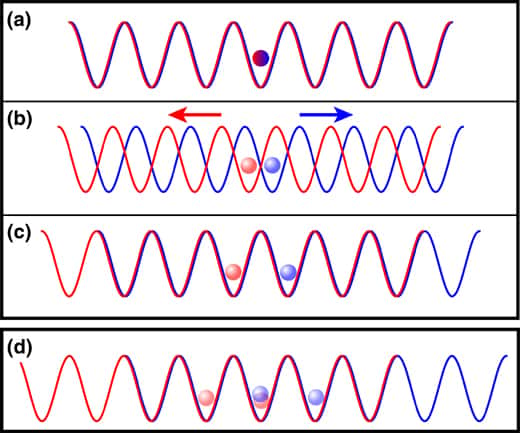
Le principe de l'expérience de marche aléatoire quantique utilisant un atome de césium et un réseau optique à lasers. Voir l'explication du schéma dans le texte. Crédit : Institut de physique appliquée, université de Bonn
Selon le prix Nobel de physique Richard FeynmanRichard Feynman, le cœur de la mécanique quantique repose sur le concept d’amplitude de probabilité. Dans le monde des atomes et des particules élémentaires, à tout processus physique imaginable correspond une amplitude de probabilité, généralement sous la forme d'un nombre complexe. Ces amplitudes interfèrent de façon mystérieuse, conduisant à des lois de probabilité d'observation de grandeurs physiques qui, bien que parfois mathématiquement semblables à celles de la physique classique, aboutissent à des phénomènes aussi étranges que l'effet tunnel ou l’intrication des particules dans l’effet EPR.
On peut illustrer de façon simple la singularité de la mécanique quantique en considérant ses prédictions pour le phénomène connu sous le nom de marche aléatoire (random walk en anglais), ou encore de marche de l'ivrogne comme l'aiment à l'appeler aussi les Anglo-saxons. Il s'agit de l'explication théorique du mouvement brownien. Pour le comprendre, il suffit de considérer une ligne sur laquelle peut se déplacer une particule et un pièce pour jouer à pile ou face.
Lançons la pièce et prenons comme règle que, selon le résultat, on déplacera la particule vers la droite ou vers la gauche. Si l'on répète un grand nombre de fois cette opération, et en supposant que les chances d'obtenir le côté pile ou le côté face sont les mêmes, l'ensemble des résultats possibles sera décrit par une loi de probabilité ayant la forme de la célèbre courbe en cloche de Gauss.
En moyenne, après N lancers de pièces, la particule sera très proche de sa position initiale, même si elle a suivi une trajectoire compliquée.
Dans un liquideliquide, le jeu des collisions aléatoires entre les particules ou entre les grains de pollenpollen, comme on voudra, conduira à l'agitation caractéristique du mouvementmouvement brownien. Dans le cas d'un ivrogne errant autour d'un réverbère, la suite de ses déplacements aléatoires, équiprobables selon toutes les directions, fera qu'en moyenne l'homme ne s'éloignera guère de son point de départpoint de départ. (Notons que, à strictement parler, l'homme n'est pas confiné autour du réverbère. Avec le temps, il finira par s'en éloigner de plus en plus, bien que moins rapidement que dans le cas quantique, car la courbe en cloche de Gauss s'applatit quand le nombre N augmente.)
Dans le monde quantique, en revanche, les choses sont différentes si l'on considère une particule ou un lancer de pièce quantique.
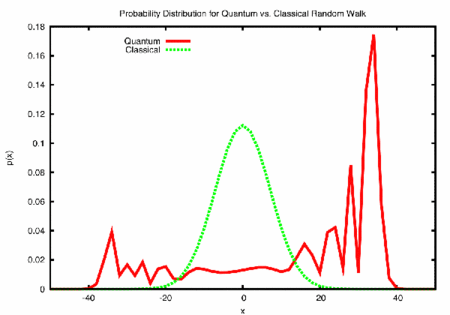
En vert, la courbe de Gauss en cloche donnant la probabilité classique de trouver la particule loin de sa position initiale après un grand nombre de lancers de pièce. En rouge, une distribution de probabilité possible pour une marche aléatoire du même type mais quantique. Crédit : Todd A. Brun
L'ivrogne quantique doit s'éloigner de son réverbère si on ne le regarde pas
S'il existe bien une amplitude de probabilité associée à un mouvement de la particule à gauche ou à droite, en l'absence d'observation de la position de la particule, les deux amplitudes coexistent et interfèrent. On est typiquement en présence de la fameuse superposition des états quantiques qui fait qu'une particule peut se retrouver simultanément en deux endroits à la fois.
Si l'on répète un grand nombre de fois l'opération de lancer de pièce quantique, toujours sans chercher à observer la position de la particule (c'est un point essentiel ), il existe une superposition complexe des amplitudes de probabilité. La particule quantique peut alors se trouver à des distances arbitrairement grandes et augmentant avec le nombre N de lancers de pièce.
Ce genre de phénomène était déjà connu du temps de Schrödinger, le découvreur de la fameuse équationéquation décrivant les ondes de matièrematière dans le monde quantique. Au départ, ce grand physicienphysicien pensait que son équation pouvait permettre de considérer les particules comme de simples paquetspaquets d'ondes, des sortes de crêtes de vaguesvagues stables sur une mer d'énergieénergie constituant un champ de matière.
Cette image particulièrement intuitive et unitaire du monde ne tarda pas à être battue en brèche par des théoriciens du calibre de Heisenberg. Ils montrèrent en effet que le paquet d'onde associé à un électronélectron devait s'étaler dans le temps et aucune individualité bien nette ne pouvait alors être associée à l'électron dans cette image purement ondulatoire.
Si l'on effectuait une observation au bout d'un certain temps, le résultat le plus probable n'était pas de trouver un électron à une distance assez proche de la position initiale du paquet d'onde mais bien de le trouver à une distance de plus en plus grande.
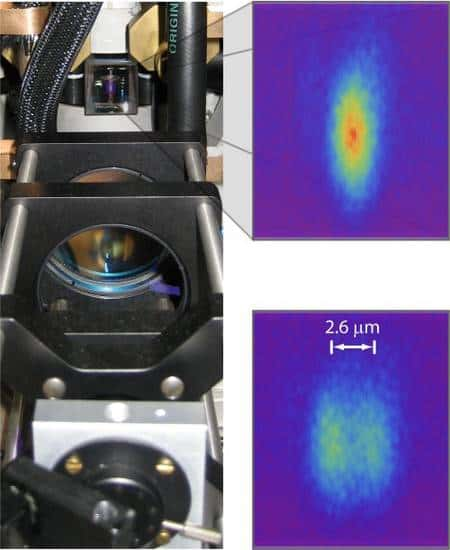
A gauche en haut se trouve la cellule en verre à ultravide où le réseau optique créé par le dispositif au premier plan piège un atome de césium et le soumet à une marche aléatoire quantique. En haut à droite, l'image montre la fonction d'onde initiale de l'atome de césium avec une probabilité de présence de plus en plus importante quand la couleur passe du bleu au rouge. En bas à droite, après un premier déphasage des lasers, la fonction d'onde de l'atome de césium indique déjà une dispersion de sa position possible.
Une belle expérience pour un théoricien, qui a aussi des applications potentielles
Une réalisation très concrète de ce phénomène vient d'être effectuée par un groupe de chercheurs de l'Institut de physique appliquée de l'université de Bonn. Les physiciens, parmi lesquels se trouve Artur Widera, ont simplement piégé un atome de césiumcésium dans un réseau optique constitué de creux et de bosses par les ondes lumineuses de plusieurs faisceaux laserlaser.
De cette manière, on peut considérer deux séries de bosses et de creux de deux sinusoïdes, une rouge et une bleue (voir les schémas en bas de l'article). En jouant sur les lasers, les deux sinusoïdes peuvent être en phase ou non.
L'atome de césium peut être traité comme une seule particule quantique et il est initialement dans un creux créé par les deux sinusoïdes en phase (schéma a).
En modifiant les faisceaux laser, on déphase lentement ces deux courbes, jusqu'à un état où les amplitudes de probabilités de la position de l'atome de césium se superposent. Ce corps a alors deux positions possibles à la suite d'une observation (schémas b et c).
En répétant l'opération, toujours sans faire d'observation entre chaque déphasage et après avoir rétabli une concordance de phase entre les deux sinusoïdes, on obtient une grande superposition quantique d'états de position (schéma d).
Au final, le plus probable sera de trouver l'atome de césium à une distance de plus en plus grande de sa position initiale au fur et à mesure qu'augmente le nombre des opérations de déphasage, les analogues du lancer de pièce.
Avec une amplitude de probabilité qui, en quelque sorte, sonde simultanément plusieurs états quantiques, ce genre d'expérience présente tout d'abord un intérêt théorique, montrant les différences entre monde quantique et monde classique. Ce travail a aussi des implications en physique de l'information quantique et même dans le domaine de la recherche d'information au sein d'une base de donnéesbase de données selon des algorithmes quantiques.
Les chercheurs allemands comme Widera imaginent même que l'on pourrait se servir de cette expérience pour mieux comprendre des processus biologiques comme la photosynthèse, qui font peut-être appel à ce genre de marche aléatoire quantique pour optimiser leur fonctionnement.