au sommaire
- À lire aussi
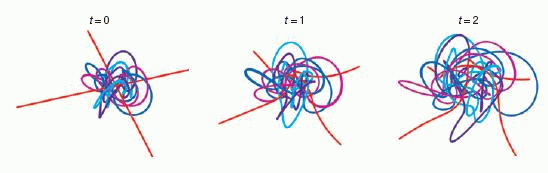
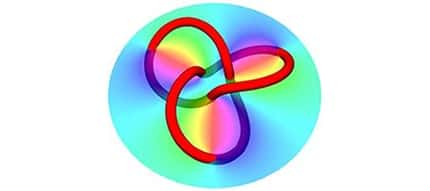
Des exemples de nœuds de lumière. Crédit : Irvine et Bouwmeester
William Irvine travaille avec le groupe de Dirk Bouwmeester à l'université de Santa-Barbara en Californie, là où œuvre également Steven Giddings, un des physiciensphysiciens ayant prédit la possible création de mini trous noirs au LHC. Irvin et son collègue Bouwmeester viennent de publier un article dans Nature dans lequel ils exposent une conclusion surprenante, issue d'une analyse mathématique profonde des célèbres équations du champ électromagnétique, découverte vers 1865 par James Clerk Maxwell.
Aussi incroyable que cela puisse paraître, ces équations possèdent des solutions correspondant à des faisceaux de lumière s'entrelaçant pour former des séries d'anneaux complexes ressemblant aux anneaux olympiques. En réalité, ce sont les lignes de champs électriqueschamps électriques et magnétiques qui adoptent ce genre de configurations stupéfiantes. Pour découvrir ces nouvelles solutions d'équations que l'on pensait bien connaître, les deux chercheurs se sont basés sur une branche extraordinaire des mathématiques, la topologie.
Baptisée la géométrie du caoutchouccaoutchouc, elle permet de classer des formes géométriques pouvant se transformer continûment les unes dans les autres. C'est ainsi qu'un topologiste ne fait pas de différence entre une tasse de café et un pneupneu de voiturevoiture. On peut en effet déformer la première en conservant un seul trou, celui de l'anseanse de la tasse, qui deviendra celui du pneu. En revanche, une sphère ne possédant pas de trou, il n'est pas possible de la déformer continûment en tore, c'est-à-dire en un pneu.
Outre de permettre de faire de la géométrie avec des objets plus complexes que des triangles et des polyèdres, cette branche des mathématiques est aussi très puissante pour démontrer des théorèmesthéorèmes d'existence et d'unicité des solutions des équations différentielles et aux dérivées partielles, omniprésentes en physiquephysique.

Dans les années 1930, un des grands noms de cette discipline toute jeune, remontant au travaux de Riemann et de Poincaré, était le mathématicienmathématicien allemand Heinz Hopf. En 1931, il découvrit une structure géométrique assez abstraite que l'on nomme la fibration de Hopf. Cette dernière a acquis une grande importance en topologie et même au-delà. On l'emploie en effet en relativité généralerelativité générale pour étudier des solutions des équations d'EinsteinEinstein et elle sert à construire la description mathématique des célèbres qubits des ordinateurs quantiquesordinateurs quantiques. Sa description nous entraînerait trop loin mais une série de vidéos remarquables, donnée en lien à la fin de l'article, permet relativement aisément au lecteur curieux de se familiariser avec la notion de fibration de Hopf.
Appliquée aux équations de Maxwelléquations de Maxwell, comme William Irvine et Dirk Bouwmeester l'ont découvert, elle implique bel et bien que des cercles de lumières enlacés sont possibles. Tout comme les récents travaux sur l’invisibilité, eux aussi basés sur une analyse puissante des équations de Maxwell, ce résultat magique prouve que même dans des domaines apparemment bien défrichés, nous ne sommes pas à l'abri de magnifiques surprises...
Les deux chercheurs réfléchissent actuellement à la manière de réaliser physiquement ces nœudsnœuds de lumière. La parenté du phénomène et des équations décrivant les tourbillonstourbillons complexes des lignes de courants dans un fluide turbulent, conduit à penser que cette découverte pourrait avoir des implications remarquables en mécanique des fluides. Ce pourrait être le cas, notamment, pour la fusion contrôléefusion contrôlée, où la stabilité de telles structures pourrait avoir son mot à dire.