au sommaire

Voilà plus d'un siècle, Joseph John Thomson (1856-1940) faisait la découverte de l'électron et mesurait sa masse. Bien avant Robert Brout, François Englert et Peter Higgs, les théoriciens de l'époque comme Lorentz et Poincaré avaient déjà entrepris de calculer la masse de l'électron. © Cavendish Laboratory, université de Cambridge
Dans son livre Le monde des particules, de l'électron aux quarks, le prix Nobel de physique Steven WeinbergSteven Weinberg explique comment son collègue Joseph John Thomson s'y est pris pour découvrir l'électron et mesurer sa masse en 1897. Weinberg ne fait pas que conter un événement important de l'histoire des sciences : il permet aux curieux et aux passionnés de physique en herbe de comprendre certains calculs simples mis en jeux dans les expériences de Thomson. Ce qu'il ne dit pas, en revanche, c'est que peu de temps après sa découverte, les théoriciens de l'époque étaient déjà occupés à calculer la masse de l’électron à partir de la théorie du champ électromagnétique.
Il était déjà clair pour eux qu'un électron devait exercer des forces électromagnétiques sur lui-même lorsqu'il était accéléré, et devait donc perdre de l'énergie et ralentir comme sous l'effet d'une force de frottement. Cela permettait de comprendre pourquoi les électrons, et plus généralement des particules chargées, émettent du rayonnement lorsqu'on les accélère. L'énergie du rayonnement provenait de l'énergie cinétiqueénergie cinétique perdue par la particule sous l'effet de ses propres forces électromagnétiques. La force d'Abraham-Lorentz, du nom de ses découvreurs, posait cependant plusieurs difficultés.

Avant 1905, le physicien Walter Kaufmann (1871-1947) avait déjà mesuré des changements de la masse d'un électron avec sa vitesse. Il n'était pas le premier à constater un changement de masse pour des corps électriquement chargés. Ses mesures viendront confirmer la théorie de la relativité. © Wikipédia, DP
Électron, force d’Abraham-Lorentz et masse électromagnétique
La première, c'est qu'elle dépend en partie de la dérivée de l'accélération, ce qui veut dire mathématiquement qu'il existe la possibilité qu'un électron s'autoaccélère. Cela pose des questions tant du point de vue de la causalité que de la conservation de l'énergie.
La seconde est que son existence impose que l'électron soit un objet dont la charge est étalée dans une petite région de l'espace. De prime abord, c'est un avantage, car en calculant l'interaction de cette charge avec elle-même, on trouvait que tout se passait comme si l'électron était doté d'une masse variant en fonction de l'inverse de la taille de la région occupée par la charge de l'électron (comme l'explique Richard FeynmanRichard Feynman dans un chapitre de son célèbre cours sur l'électromagnétisme, désormais en accès libre). On pouvait donc expliquer la masse de la matièrematière.
Remarquablement, cette masse d'un électron devait varier avec la vitessevitesse de son déplacement selon une formule identique à celle que va découvrir Albert EinsteinEinstein avec sa théorie de la relativité restreinte en 1905, qui en donnera une portée plus générale et une tout autre origine : l'espace-tempsespace-temps. Cette variation commençait déjà à être observée expérimentalement avant les travaux d'Einstein, comme le mentionne Lorentz en 1902 dans son allocution pour la réceptionréception de son prix Nobel. Un gain de précision dans la mesure de la masse des électrons dans certaines situations, en l'occurrence avec de grandes vitesses, avait donc révélé la pointe émergée d'une révolution en physique fondamentale.

Le prix Nobel Hans Georg Dehmelt a fait avancer la physique en créant l'une des techniques permettant de piéger des ions et des particules isolées pour en étudier les propriétés. C'est lui qui a donné au piège de son invention le nom du physicien Frans Michel Penning. Les pièges à ions sont utilisés de nos jours pour étudier la faisabilité des ordinateurs quantiques ou encore les propriétés des antiprotons. © Mary Levin, University of Washington
Le casse-tête des masses des particules quantiques
Malheureusement, les modèles étendus de l'électron souffriront de divers problèmes. Surtout, les premiers développements de la version quantique et relativiste de la théorie de Maxwell-Lorentz, l'électrodynamique quantiqueélectrodynamique quantique relativiste (quantum electrodynamics ou QED en anglais), vont faire apparaître des quantités infinies dans les calculs, notamment ceux de la masse dite électromagnétique d'une particule chargée. De la fin des années 1930 à celle des années 1940, Victor Weisskopf, Julius Schwinger, Sin-Itiro Tomonaga et Richard Feynman vont trouver des règles de calcul permettant de dompter les infinis de la QED, mais sans jamais vraiment résoudre le problème. Ses règles, que l'on rassemble sous le nom de théorie de la renormalisation parce qu'elles permettent notamment d'extraire des théories des champs des valeurs finies pour la masse et la charge des particules, ont reçu des justifications mathématiques et physiques plus satisfaisantes grâce aux travaux d'un autre prix Nobel, Kenneth Wilson.
Malgré tout, l'origine exacte de la masse d'un électron reste finalement mal comprise, comme celles des autres particules de matière considérées comme élémentaires, tels le muonmuon, les neutrinosneutrinos et les quarksquarks. Le mécanisme de Brout-Englert-Higgs, via les couplages de Yukawa, a tout de même permis de faire des avancées significatives.
Ce qui est sûr, c'est que de la nouvelle physique, comme la supersymétriesupersymétrie ou une théorie de gravitation quantique, doit entrer en jeu et sans doute trahir sa présence si l'on mesure avec suffisamment de précision la masse d'un électron. Les physiciensphysiciens continuent donc à vouloir gagner des décimales dans la détermination de la valeur de cette masse. Un bon exemple de ce qui pourrait arriver est que la masse d'un électron puisse changer lentement au cours de l'histoire de l'universunivers. La théorie des cordes offre cette possibilité, et on a donc cherché des phénomènes pouvant trahir des changements à quelques milliards d'années d'intervalle. Une bonne fenêtrefenêtre d'observation consiste à mesurer des spectresspectres en astrophysiqueastrophysique reliés au rapport entre la masse de l'électron et celle du protonproton. Aucune trace de variation n'a encore été trouvée, mais il suffira peut-être de pousser d'un cran plus loin la précision des mesures. Cela suppose aussi de le faire avec la masse de l'électron, que l'on mesure aujourd'hui dans des laboratoires sur Terre.
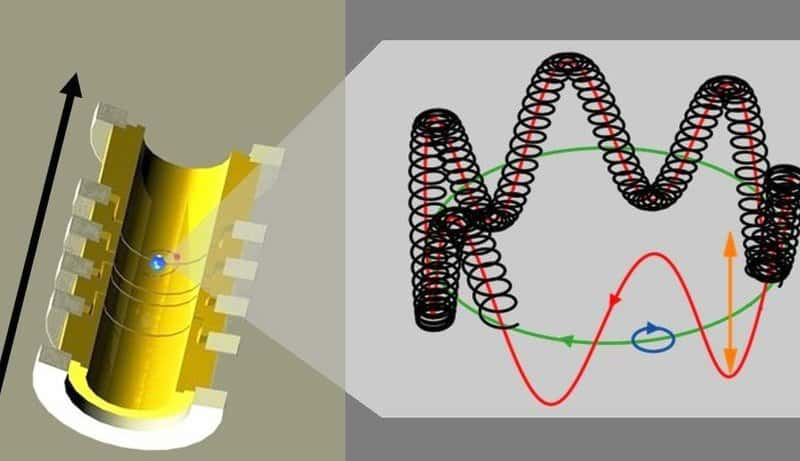
Dans un piège de Penning, un champ magnétique uniforme conduit un ion à effectuer des mouvements circulaires dans un même plan (vert et bleu) en conjonction avec un mouvement d'oscillation vertical (rouge) sous l'action d’un champ électrostatique. La direction et l'orientation du champ magnétique sont indiquées par la flèche noire à gauche. © Sven Sturm
Les particules individuelles piégées, un laboratoire pour la physique
Comme le montre une publication dans Nature, cela vient d'être fait par une équipe de physiciens allemands. Les chercheurs ont utilisé pour cela un piège à ions très connu en physique, appelé piège de Penning. Bien que l'inspiration pour ce piège remonte aux travaux du physicien néerlandais Frans Michel Penning, sa première réalisation est due au prix Nobel de physique Hans Georg Dehmelt. Dans un piège de Penning, un champ magnétiquechamp magnétique uniforme conduit une particule chargée à effectuer des mouvementsmouvements circulaires dans un plan perpendiculaire à ce champ magnétique, pendant qu'un champ électrostatiqueélectrostatique fait osciller la particule de part et d'autre de ce plan. Il en résulte un mouvement général faisant intervenir trois fréquencesfréquences.
Dans l'expérience ayant conduit à la détermination très précise de la masse de l'électron, un atomeatome de carbonecarbone presque totalement ionisé a été piégé. Il ne restait plus qu'un unique électron en orbiteorbite autour du noyau. Cet électron possède un spinspin qui peut effectuer un mouvement de précessionprécession dans un champ magnétique, mais aussi basculer sous l'effet d'un faisceau de micro-ondes. Ces divers mouvements du noyau et de l'électron sont parfois reliés, ce qui permet de mesurer diverses quantités. Les chercheurs avaient précédemment mesuré de cette façon le facteur de Landé de l'électron, un test de la QED. Cette fois-ci, ils ont mesuré la masse de l'électron par rapport à celle du proton.
Le gain de précision obtenu est de l'ordre d'un facteur 13, de sorte que la masse du proton vaut désormais 1.836,15267377 fois celle de l'électron. La balle est maintenant dans le camp des théoriciens.