au sommaire
Mécanique quantique : fondements et applications
La relation vertueuse (mais parfois orageuse) entre mathématiques et physique est pleine de surprises. Ainsi, certains objets mathématiques, considérés d'abord comme de simples curiosités, finissent par jouer un rôle dans l'explication de phénomènes physiques.
Les bizarreries et la sagesse des particules
L'une des étrangetés quantiques les plus connues est l'effet tunnel. Tout le monde sait qu'une balle lancée sur un murmur rebondit et repart en arrière. Faites l'expérience avec un électron (avec le mur qu'il faut) et, ô stupeur, il existe une certaine probabilité de trouver l'électron de l'autre côté du mur.
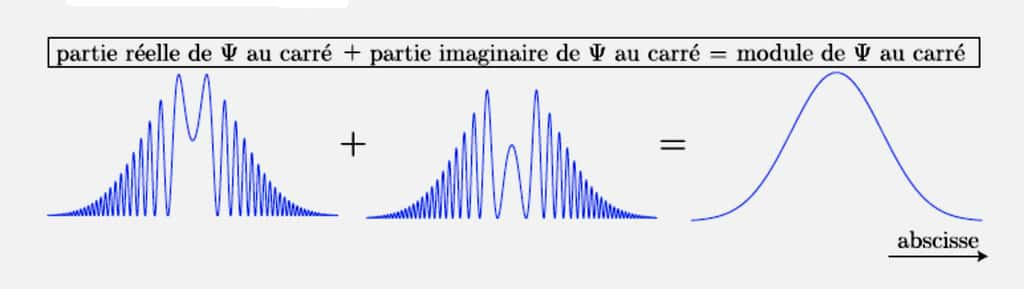
La complexité de la fonction d'onde
À n'en pas douter, la fonction d'onde Ψ de Schrödinger a jeté un pavé dans la mare du réel des physiciensphysiciens. Sa complexité ne réside pas seulement dans son étrange signification et ce qu'elle permet de prévoir par le calcul.
Une autre invraisemblance de la théorie quantique est la négation de l'existence d'une trajectoire pour une particule (l'expérience des fentes d'Young est là pour s'en convaincre).
Le facteur anormal de l'électron ou la précision du diable
L'électron possède un moment magnétique (il n'est pas le seul) dont l'origine est longtemps restée très énigmatique, mais qui s'est révélé être lié à un moment cinétique propre (le spinspin).
L'effet Mössbauer ou le canon sans recul
On a tous appris, par l'expérience quotidienne ou par la connaissance académique de la conservation de l'impulsion (quantité de mouvementquantité de mouvement), que quand on va d'une extrémité à l'autre d'une barque sur un lac, la barque se déplace en sens contraire.
C'est sans doute l'une des applicationsapplications les plus inimaginables pour Heisenberg et Schrödinger, pour lesquels la constructionconstruction nécessaire d'une nouvelle théorie visait à comprendre le mécanisme de la lumièrelumière émise par les atomesatomes.
Tout le monde a au moins une perception intuitive de ce que l'on appelle une fonction (numériquenumérique) : on se donne une suite de règles -- une recette -- permettant de fabriquer un deuxième nombre, X, à partir d'un premier x.
Les distributions, ou comment donner un sens à des objets qui n'en ont pas
On vient de parler de fonctions, au sens élémentaire. Dans les premières décennies du XXe siècle, la nécessité est apparue de généraliser cette notion.
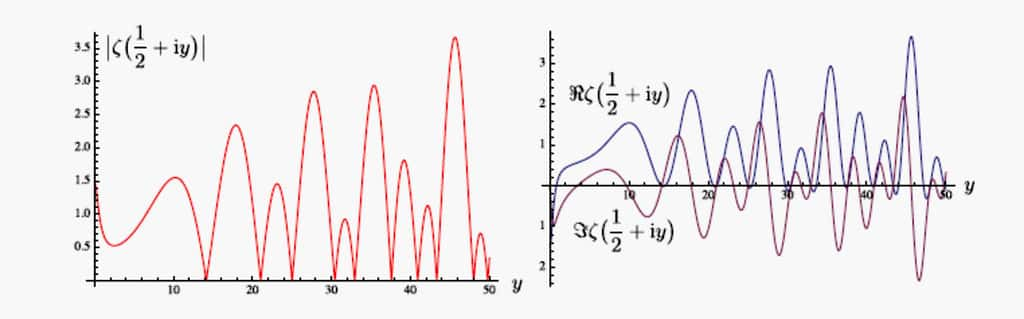
En 1859, dans un article à propos de l'étude de la fonction portant son nom, Bernhard RiemannBernhard Riemann glissa entre deux lignes une affirmation dont il jugea la démonstration superflue pour ce qu'il était en train de faire.
Le chaos, au sens banal du terme, est à la mode, trop souvent mis à toutes les sauces. Pour les scientifiques, il s'agit d'un nouvel ordre, insoupçonné pendant des siècles de déterminisme triomphant.
Le calcul sur machine : merveilles et canulars
Les ordinateursordinateurs ont envahi notre quotidien, pour accomplir des tâches répétitives ou « managériales » qui n'ont rien de scientifique, mais aussi pour seconder l'esprit de qui entreprend une modélisationmodélisation quantitative sous une forme ou sous une autre.
Des mathématiques pour les sciences, un livre de Claude Aslangul
À découvrir aux éditions De Boeck, Des mathématiques pour les sciences, un ouvrage de Claude AslangulClaude Aslangul.