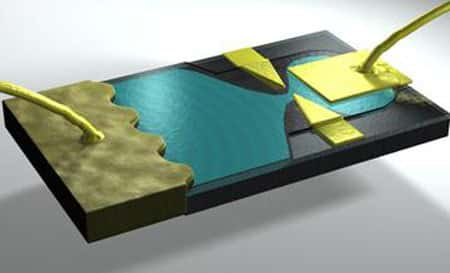
Vue d'artiste d'un circuit RC quantique réalisé dans un gaz d'électrons bidimensionnel (en bleu) à l'interface de deux semi-conducteurs (gris clair et gris foncé). Le gaz est connecté d'un côté à une armature métallique (jaune foncé) et couplé capacitivem
Ces résultats sont publiés dans la revue Science. Les chercheurs ont montré que les lois fondamentales de l'électricité, établies depuis 1845, ne peuvent plus décrire les propriétés d'un circuit électronique lorsque ses dimensions atteignent l'échelle nanométrique. Ces études confirment des prédictions théoriques de Markus Büttiker (université de Genève) énoncées il y a plus de dix années et jamais encore vérifiées.
Les lois de la physique macroscopique ordinaire ne rendent pas compte du comportement microscopique des électrons, régi par les lois de la mécanique quantique. Cette mécanique, depuis sa découverte il y a près de 100 ans, a révélé des comportements tout à fait étonnants s'écartant de notre compréhension intuitive des phénomènes. Due à la miniaturisation des circuits électroniques, la taille des composants devient si petite que la description physique des phénomènes en jeu en est affectée : les lois de la physique macroscopique ne sont plus applicables. Les effets quantiques seront incontournables dans les circuits de l'électronique de demain.
Les chercheurs ont étudié un circuit quantique composé de la mise en série de deux composants nanométriques, une résistancerésistance quantique R et une capacité quantique C. Pour fabriquer de tels nanocomposants, les chercheurs délimitent par nanolithographie une constriction (l'équivalent d'un fil ultra-mince) et un condensateur dont les dimensions sont réduites à quelques dizaines de nanomètres. Les propriétés du circuit résultant de l'association de deux composants obéissent habituellement aux lois d'additivité dites de Kirchoff. Les chercheurs ont montré que ce n'était plus vrai pour ce circuit quantique. Ils ont ainsi identifié deux propriétés particulièrement intéressantes :
1) Dans un circuit classique, l'impédance (effet combiné de la résistance et de la capacité) de deux composants en série est la somme des impédances de chacun. Or, les chercheurs ont mesuré sur leur circuit quantique une résistance équivalente en moyenne deux fois plus petite. Un tel circuit va donc pouvoir fonctionner deux fois plus vite que ce qu'on aurait pu attendre. C'est une bonne nouvelle !
2) De manière encore plus remarquable, pour un circuit classique R seul, la diminution du diamètre du fil conduit à l'augmentation de sa résistance. Dans le cas de ce circuit quantique, la résistance équivalente reste constante quelle que soit la constriction (et est bien plus faible que la nanorésistance mesurée seule).
Cette découverte est fondamentale dans la connaissance des effets de transport de charges électriques dans des nano-objets semi-conducteurssemi-conducteurs (transistors à nanotubes de carbonenanotubes de carbone par exemple) qui seront à la base de l'électronique de demain et pour lesquels les formules d'association de circuits ne seront plus les mêmes. Cette découverte peut aussi jouer un rôle fondamental dans le domaine de l'électronique moléculaire, permettant de mieux comprendre l'équivalent électronique d'une moléculemolécule ou d'un circuit moléculaire via son circuit quantique équivalent.
Références :
Consulter le site web
Contacts :
Chercheurs
CNRS
Bernard Plaçais
TT 01 44 32 34 56
placais@lpa.ens.fr
ENS
Jean-Marc Berroir
T 01 44 32 33 61
berroir@lpa.ens.fr
CEA
D. Christian Glattli
T 01 44 32 25 24
christian.glattli@cea.fr
CNRS
Martine Hasler
T 01 44 96 46 35
martine.hasler@cnrs-dir.fr
CEA
Pascal NewtonNewton
T 01 64 50 20 97
pascal.newton@cea.fr