EinsteinEinstein a souvent été présenté comme un physicienphysicien génial avant son arrivée à l'université de Princeton au début des années 1930, puis comme une victime de l'âge et de la « fossilisationfossilisation » (selon ses termes) par la suite, ne comprenant rien à la révolution quantique.

C'est complètement faux. Non seulement il a été l'un des fondateurs de la première heure de la théorie quantique, mais même après 1930 ses tentatives pour aller au-delà de la théorie quantique orthodoxe ont pavé la voie de la révolution moderne concernant l'information quantique via sa découverte, avec Schrödinger, du phénomène de l'intrication quantique.

De nos jours, les expériences faites pour tester le phénomène de l'intrication quantique et l'utiliser, par exemple pour faire de la téléportation d'états quantiques ou de la cryptographiecryptographie, reposent sur la mesure de la polarisation de paires de photons jumeaux, ou sur le spin de paires d'électrons jumeaux. Mais en 1935, lorsque Einstein, Podolsky et Rosen (EPR) ont publié leur célèbre article pour tenter de démontrer que la théorie quantique orthodoxe devait être incomplète et laisser la place à une théorie plus profonde, il en était tout autrement.

Pour comprendre l'expérience de pensée proposée par ces trois chercheurs, il faut savoir qu'en mécanique quantique, des grandeurs physiques, comme la quantité de mouvementsquantité de mouvements et la position d'une particule, sont décrites par des objets mathématiques appelés « opérateurs ». Il s'agit de grandeurs mathématiques qui obéissent à une algèbre inhabituelle pour des nombres ordinaires, leur produit ne commute pas nécessairement. On peut souvent, mais pas toujours, se les représenter sous forme d'une matrice pour chaque opérateur, un tableau de nombres.

Un défi aux inégalités de Heisenberg position-impulsion

Cette non-commutativité impose alors, que lorsque l'on considère un objet avec des grandeurs physiques associées sous forme d'opérateurs, il n'est pas possible de mesurer simultanément précisément ces grandeurs. Pire, la théorie dénie même l'existence simultanée des valeurs ces deux grandeurs.

Ainsi, avec un quanta de matièrematière ou de lumièrelumière, on ne peut non seulement pas connaître la position et la quantité de mouvements de cette particule avec une précision infinie, mais la position et la quantité de mouvements au sens classique ne sont pas des caractéristiques possédées simultanément par la particule. Cet interdit est bien exprimé par les fameuses inégalités de Heisenberginégalités de Heisenberg.

Ce comportement étrange indique en réalité que dans le monde quantique il n'existe pas vraiment de particule au sens classique du terme, qui pourrait ressembler à une boule de billard. Il existe un objet, un quanta de matière ou de lumière, qui, selon la situation expérimentale, peut être décrit en partie avec des images de position et de quantité de mouvements, mais sous réserve que ces images n'existent pas simultanément.

Pour des gens comme Einstein et Schrödinger, une telle situation ne reflétait qu'une impuissance momentanée de la théorie quantique à fournir une image claire et précise de ce qu'il fallait entendre par un quanta de lumière ou de matière dans l'espace et le temps. C'est pour le prouver qu'Einstein et ses collaborateurs, Podolski et Rosen, proposèrent donc, en 1935, un moyen de violer les inégalités de Heisenberg avec une expérience de pensée conduisant à ce que l'on a depuis appelé le paradoxe EPRparadoxe EPR ou encore l'effet EPR.

Une particule décrite par une seule fonction d'onde Ψ (x1, x2) se désintègre par exemple en deux électrons (en noir et en rouge sur ce schéma). A priori, des mesures sur l'un, lorsqu'une grande distance les sépare, ne peuvent influer sur l'état de l'autre plus vite que la lumière. La mécanique quantique réfute cette conclusion. © Soshichi Uchii

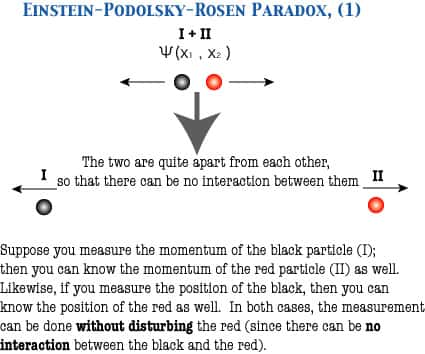
Pour cela, ils ont considéré une particule au repos décrite par une fonction d'onde Ψ, la fameuse fonction donnant l'amplitude de probabilité de trouver un système physique dans un état donné, par exemple de position, d'énergieénergie, de spin, etc. Le carré de cette fonction permet de trouver la probabilité, de trouver les valeurs de ces grandeurs physiques dans les résultats des expériences que l'on peut mener et finalement de calculer des valeurs moyennes pour ces grandeurs.

La particule se désintègre en donnant deux autres particules, par exemple un électron et un positronpositron se déplaçant presque à la vitesse de la lumièrevitesse de la lumière et qui sont précisément dans un état que l'on décrit aujourd'hui par le terme d'intrication quantique. La conservation de la quantité de mouvements fait que positron et électron partiront dans des directions opposées et avec des quantités de mouvements identiques en valeur absolue.

Mesurons précisément la quantité de mouvements d'une des particules (par l'exemple la noire sur les deux schémas). On connaît a priori instantanément la valeur de l'autre (rouge). Réalisons simultanément une mesure de la position sur la deuxième particule. On devrait pouvoir aussi connaître sa position avec la précision désirée.

Il semble donc que l'on ait violé les inégalités de Heisenberg, à moins d'imaginer un signal envoyé par le premier électron vers l'autre pour brouiller toute mesure de sa position. Mais si l'on considère la mesure de la quantité de mouvements du premier électron six mois après son émissionémission, pour respecter la théorie quantique, il faut que le signal rejoigne instantanément - ou pour le moins plus vite que la lumière - le second électron à une année-lumièreannée-lumière de là. On obtient donc une contradiction avec la relativité restreinte, indiquant un problème dans la théorie quantique et donc la nécessité de la modifier.

Les deux électrons ne peuvent pas être considérés comme deux systèmes séparés décrits par deux fonctions d'onde de la forme Ψ(x1) Ψ(x2), il y a intrication, et l'on ne peut violer les inégalités de Heisenberg. On pourrait penser mesurer l'impulsion p de la particule I et la position q de la particule II avec une précision illimitée. On en déduirait la position et l'impulsion de la particule II là aussi avec une précision illimitée mais la mécanique quantique, via l'intrication, l'interdit. © Soshichi Uchii

C'est du moins ce qu'Einstein pensait mais Niels BohrNiels Bohr n'a pas tardé à contrer cet argument en répliquant qu'il n'était pas possible de parler de phénomènes physiques ni d'objets possédant telle ou telle propriété, indépendamment de la situation expérimentale dans le formalisme de la théorie quantique.

Ainsi, dans l'exemple précédent, électron et positron sont en fait intriqués et ne sont pas décrits par deux fonctions d'ondes indépendantes avant toute mesure. Il n'existe qu'une seule fonction globale, un seul objet, et on ne peut pas parler de deux objets séparés dans l'espace et dans le temps.

L'ensemble réagit d'un bloc lors d'une mesure, quelles que soient les distances, et exhibe une non-localité. Cette dernière propriété est malgré tout en accord avec la relativité restreinterelativité restreinte car le flou quantique interdit de pouvoir prédire le résultat des deux mesures. On ne peut pas s'en servir pour transmettre de l'information directement et quasi-instantanément car on ne contrôle pas le résultats des mesures.

John Bell devant le tableau noir dans son bureau au Cern. On peut y voir tout en haut la fameuse inégalité qu'il a démontrée en 1964, au-dessus d'un schéma montrant le principe de l'expérience réalisée en 1982 avec des paires de photons polarisés par Alain Aspect et ses collègues. © Cern

L'inégalité de Bell, un test de la présence de l'intrication quantique

Le débat était purement théorique au sujet de l'effet EPR dans les années 1930 mais dans les années 1960, est entré en lice le physicien John BellJohn Bell qui a montré dans un article - en prenant une nouvelle version de l'expérience EPR - qu'il était possible de départager Einstein et Bohr, au moins jusqu'à un certain point.

L'article de Bell prenait comme base le travail du physicien David Bohm qui avait transposé le raisonnement EPR, portant initialement sur la mesure des positions et des vitesses d'une paire de particules de matière intriquées, à la mesure des spins de ces particules. Plus tard, David Mermin montra que l'on pouvait faire de même en mesurant la polarisation d'une paire de photons intriqués. C'est précisément de cette façon que les idées de Bell ont pu être mises en pratique par Alain Aspect et ses collègues Philippe Grangier, Gérard Roger et Jean Dalibard au moyen d'une expérience conduite à l'université d'Orsay en 1982. Niels Bohr est sorti victorieux de cette expérience, bien que le dernier mot au sujet de la mécanique quantiquemécanique quantique ne soit pas encore dit et que l'on pourrait bien découvrir un jour qu'Einstein avait fondamentalement raison, mais sous une forme très sophistiquée.

Toujours est-il que depuis lors, la majorité des expériences permettant de tester l'effet EPR se font avec des mesures de grandeurs physiques qui ne peuvent prendre que des valeurs discrètes, en l'occurrence, celles du spin de particules mises en jeu. Ces valeurs constituent ce que l'on appelle le spectrespectre des opérateurs associés aux grandeurs physiques. Dans le cas des mesures de positions et de quantités de mouvements, les spectres sont continus.

Bell avait déduit une célèbre inégalité, portant son nom, concernant les résultats des mesures d'un effet EPR avec des variables discrètes. Or, il se trouve que l'on soupçonne que l'intrication quantique apparaît dans bien plus de phénomènes qu'on ne pourrait le penser. Elle pourrait jouer un rôle considérable en biologie quantique et même en cosmologie, voire dans le fonctionnement du cerveau.

Comme d'autres avant eux, deux physiciens de l'université Purdue (West Lafayette, États-Unis), Junxu Li et Sabre Kais pensent que l'on doit pouvoir trouver des effets de l'intrication quantique dans des réactions chimiquesréactions chimiques. Mais tout comme dans le cas de l'effet EPR initial, cela suppose de faire des mesures avec des opérateurs dont les spectres sont continus. Or, comme on l'a vu, les résultats des travaux de Bell, qui permettent de mettre en évidence des effets d'intrication, sont plus facilement exprimables et testables expérimentalement avec des spectres discrets de valeurs.

Les deux chercheurs ont donc entrepris de découvrir, et avec succès, une généralisation pour l'instant encore théorique des travaux de Bell qui permettraient de faire des tests d'intrication avec les variables continues des atomesatomes et moléculesmolécules intervenant dans des réactions chimiques (une généralisation des travaux de Bell dans le cas continu avait déjà été obtenue avec des paquetspaquets de photons). On peut comprendre basiquement l'idée quand on se représente par exemple l'inverse de la désintégration d'une particule en deux particules précédemment envisagée. On a alors par exemple deux atomes qui entrent en collision pour former une molécule. Plus généralement, on peut envisager des collisions de molécules donnant par redistribution des atomes d'autres molécules.

Junxu Li et Sabre Kais viennent de publier dans Science Advances les résultats de leurs travaux à ce sujet dans un article dont une version est aussi disponible sur arXiv. Sabre Kais explique donc que : « Personne n'a encore démontré expérimentalement la présence de l'intrication quantique dans des réactions chimiques parce que nous n'avions pas le moyen de la mettre en évidence. Pour la première fois, nous avons un moyen pratique de mesurer cet effet. La question est maintenant de savoir si nous pouvons utiliser l'intrication quantique à notre avantage pour prédire et contrôler le résultat des réactions chimiques. »

Les deux physiciens ont fait passer un test théorique à l'inégalité généralisée de Bell qu'ils ont obtenue dans une simulation numériquesimulation numérique de la physique quantiquephysique quantique d'une réaction chimique conduisant à la molécule d'hydrure de deutérium (HD), à partir d'une expérience de collision de molécules H₂ et D_2. Une expérience déjà menée par des chercheurs de l'université de Stanford, visant à étudier les états quantiques des interactions moléculaires.

Ils sont confiants qu'en répétant une expérience similaire, et en analysant les résultats avec leur nouvelle méthode, la présence de l'intrication quantique sera révélée.

L’intrication quantique observée sur des objets presque macroscopiques

Article de Nathalie MayerNathalie Mayer publié le 06/05/2018

L'une des manifestations les plus incroyables de la physique quantique est probablement celle que l'on appelle l'intrication. Et après l'avoir observée sur des électrons et des atomes, des chercheurs affirment aujourd'hui en avoir été témoins sur des objets de taille presque macroscopique.

L'intrication quantique. Un phénomène étrange par lequel deux objets distants se retrouvent comme liés - par des états quantiques dépendants l'un de l'autre - d'une manière qui défie le sens commun et même la physique classique. Et pour la toute première fois, des scientifiques ont pu obtenir et observer ce phénomène sur des objets macroscopiques. Enfin presque. Des objets dont le diamètre est de l'ordre de 15 micromètresmicromètres.

Jusqu'alors, l'intrication quantique n'avait pu être montrée que sur des particules. En 2015, par exemple, des chercheurs du MIT avaient réussi à intriquer, grâce à une impulsion laserlaser, pas moins de 3.000 atomes de rubidiumrubidium 87. Une broutille face aux milliards de milliards d'atomes que composent les oscillateurs mécaniques du diamètre approximatif d'un cheveu humain, impliqués dans l'expérience qui vient d'être menée par des chercheurs de l'université de Aalto (Finlande).

Une équipe a en effet réussi à placer ces sortes de peaux de tambours vibrants en aluminiumaluminium dans un état quantique intriqué. Un état qui a pu être maintenu pendant pas moins d'une demi-heure. « Les corps vibrants interagissent via un circuit hyperfréquence supraconducteursupraconducteur. Les champs électromagnétiqueschamps électromagnétiques dans le circuit sont utilisés pour absorber toutes les perturbations thermiques et ne laisser derrière que les vibrationsvibrations quantiques mécaniques », explique Mika Sillanpää. Et le fait de conduire l'expérience à une température juste au-dessus du zéro absolu, aux environs de -273 °C donc, a permis d'éviter toute autre forme de perturbations et d'interférencesinterférences.

Téléporter les propriétés physiques d’un objet macroscopique comme dans certains films de science-fiction grâce à l’intrication ? « Nous en sommes encore loin », reconnaissent les chercheurs. © tombud, Pixabay, CC0 Creative Commons

La physique quantique aussi valable à notre échelle ?

Car, si rien dans la mécanique quantique n'impose formellement qu'elle ne s'applique qu'à des objets de petite taille, deux facteurs semblent cruciaux lorsqu'il s'agit de déterminer si oui ou non un objet se comportera selon les règles étranges de la physique quantique. Ainsi, pour entrer dans le monde de la mécanique quantique, un objet devra d'abord pouvoir s'isoler des perturbations de son environnement. Il faudra ensuite que l'énergie associée à cet objet - sa fréquencefréquence de vibration - dépasse l'énergie associée à son environnement - sa température. C'est pourquoi les petits objets sont plus susceptibles d'être soumis aux règles de la physique quantique.

D'un point de vue fondamental, cette expérience démontre donc que les lois de la mécanique quantique peuvent aussi s'appliquer à des objets « massifs ». Restera à déterminer massifs à quel point. D'un point de vue plus pratique, l'expérience pourrait, entre autres, servir à optimiser la détection d'ondes gravitationnelles.

Notez par ailleurs qu'un autre groupe, issu cette fois de l'université de Delft (Pays-Bas), a également annoncé avoir réussi à placer des objets de la taille de bactériesbactéries en état d'intrication quantique : deux oscillateurs micromécaniques à base de rayons de siliciumsilicium nanostructurés sur des puces espacées de 20 centimètres. Une configuration intéressante en vue d'une intégration au sein d'un réseau quantique à fibre optiquefibre optique. Mais l'état d'intrication n'a toutefois pas pu être maintenu plus d'une fraction de seconde.