au sommaire
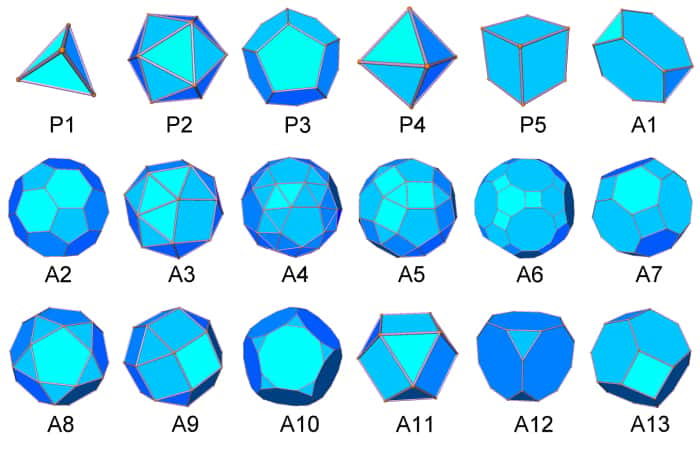
En haut, les 5 solides platoniciens (P1 à P5) et ensuite les 13 solides archimédiens (A1 à A13). Crédit : S. Torquato et Y. Jiao
Le problème du pavage de l'espace par des solides réguliers est la généralisation de celui du plan par des polygones réguliers, comme des triangles isocèles ou des carrés. Cela peut sembler un problème de mathématique pur mais il a des répercussions sur la physique des solides.
On peut s'en douter en considérant le problème des oranges que l'on peut faire remonter à Képler, même si celui-ci considérait des empilements de boulets de canon. En effet, en considérant les boulets comme des atomes, il devient possible de relier la taille et l'empilement de ces derniers à la densité d'un matériaumatériau donné et donc de mieux comprendre et de mieux concevoir des matériaux avec des propriétés physiques remarquables.
De nos jours, et pour les mêmes raisons, un groupe de chercheurs de Princeton s'est de nouveau attelé à déterminer le pavage de l'espace le plus efficace avec des polyèdres réguliers et d'autres dits semi-réguliers. Dans le premier cas il s'agit des célèbres solides platoniciens, dont on pense qu'ils permettent de mieux comprendre le verre, et dans le second cas les chercheurs de Princeton, parmi lesquels se trouve Salvatore Torquato, ont en fait considéré une classe particulière de polyèdres semi-réguliers : les polyèdres d'Archimède.
Avec Yang Jiao, un étudiant de thèse du Department of Mechanical and Aerospace Engineering, Torquato vient de publier un article dans Nature dans lequel il annonce avoir battu le record du pavage de l'espace avec des tétraèdres, détenue depuis l'année dernière par Elizabeth Chen, une autre étudiante en thèse de l'Université du Michigan.
En utilisant un nouvel algorithme sur ordinateurordinateur, les deux chercheurs sont en effet parvenus à trouver un pavage occupant 78,2 % d'un volumevolume donné au lieu des 77,8 % précédemment obtenus par Chen.
Des jeux mathématiques aux conséquences bien concrètes
Plus généralement, puisqu'il considère des pavages avec les 5 solides platoniciens et les 13 solides archimédiens, leur nouvelle méthode ouvre de larges perspectives dans de nombreux domaines. Des agglomérats d'atomes ou de moléculesmolécules prennent naturellement des formes de solides platoniciens et archimédiens à très basses températures, ou dans le cas de molécules complexes subissant différents changements de phase.
Mais ce n'est pas tout, des problèmes d'optimisation de pavage de l'espace avec des solides de ce genre sont mathématiquement reliés à des codes de détection et de corrections d'erreur utilisés pour enregistrer des informations sur des disques compactes, ou pour comprimer ces dernières et optimiser leur transfert par les moyens de télécommunications.
Les conséquences de ces simples jeux mathématiques sur notre vie de tous les jours pourraient bien se révéler importantes un jour ou l'autre.
























