au sommaire

Wendelin Werner
Les marches aléatoires et le mouvement brownien
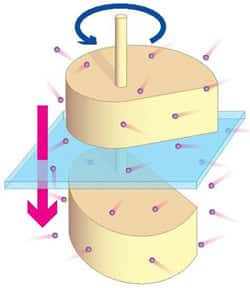
En 1828, le naturaliste écossais Richard Brown publie un opuscule concernant l'agitation incessante et spontanée de petites particules contenues dans le pollenpollen : l'étude de ce phénomène singulier a donné lieu à un concept mathématique, baptisé mouvement brownien. Pour définir ce dernier, donnons-nous une particule mobilemobile assignée à se déplacer le long d'un quadrillage du plan. A la première étape la particule est en un point donné (en rouge sur la figure) et on tire au hasard une direction : la particule se déplace alors jusqu'à un nouveau nœud du maillage et on peut itérer le processus. La trajectoire de la particule forme ainsi une courbe, appelée marche aléatoire, qui est d'autant plus complexe que le nombre d'étapes augmente. Mais si de plus on décide de prendre des quadrillage plus fins, le comportement erratique s'accentue considérablement pour donner in fine (c'est-à-dire en faisant tendre le pas du quadrillage vers zéro) un " objet limite " complexe : le mouvement brownien.
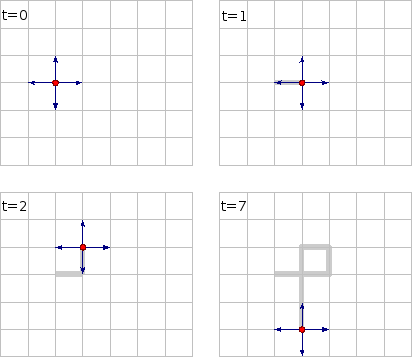
Sur un réseau (ici carré), une particule se déplace au hasard : sa trajectoire est une marche aléatoire.
Crédits : Salvatore Tummarello
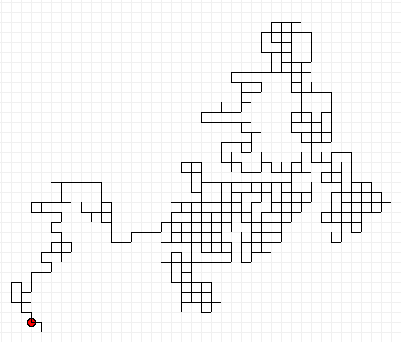
Marche aléatoire : pas de 10 pixels , 1 000 itérations.
Crédits : Salvatore Tummarello
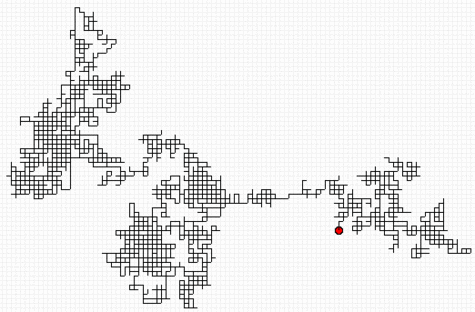
Marche aléatoire : pas de 5 pixels , 5 000 itérations.
Crédits : Salvatore Tummarello
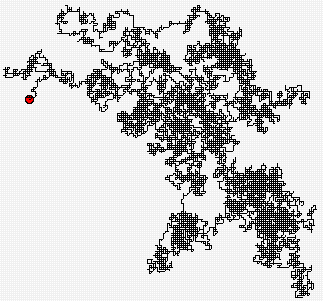
Marche aléatoire : pas de 2 pixels , 25 000 itérations.
Crédits : Salvatore Tummarello

Mouvement brownien : pas de 1 pixel , 200 000 itérations.
Crédits : Salvatore Tummarello
La dimension fractale
Parmi les résultats importants obtenus par W. Werner et ses collaborateurs (G. Lawler et O. Schramm) figure la démonstration d'une conjecture énoncée par B. Mandelbrot en 1982 : la frontière d'un mouvement brownien est toujours de dimension fractale égale à 4/3. Elaborée par B. Mandelbrot, la dimension fractale d'une courbe étend à des nombres non nécessairement entiers la notion de dimension usuelle en géométrie, à savoir le nombre de coordonnées nécessaires pour repérer un point : il faut par exemple trois coordonnées dans l'espace (pour la longueur, la largeur et la hauteur), tandis qu'il en suffit de deux pour la sphère (latitudelatitude, longitudelongitude). Nous renvoyons au dossier de J.-P. Louvet pour plus d'informations au sujet de la dimension fractale. Ce qui est remarquable dans ce désormais théorème est que le mouvement brownien, issu d'un hasard microscopique, vérifie une propriété forte de régularité macroscopique.
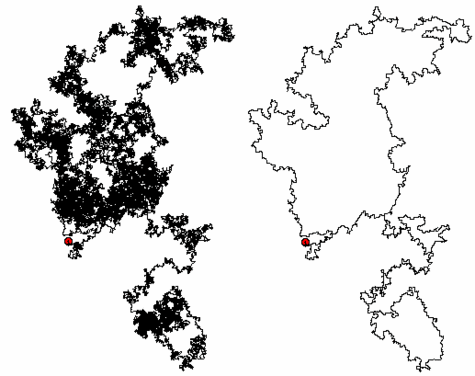
Un mouvement brownien et sa frontière à droite : la dimension fractale de cette courbe vaut 4/3.
Crédits : Salvatore Tummarello
La percolation
W. Werner ne s'est pas seulement intéressé au mouvement brownien : un autre modèle, la percolationpercolation, fournit d'autres exemples de " courbes planes aléatoires ". Le principe de la percolation est relativement simple : en se donnant un réseau (par exemple en " nid d'abeilles " comme sur la figure suivante), on parcourt l'ensemble des cellules (ici, hexagonales) en choisissant pour chacune de la griser ou non en tirant à pile ou face. La figure obtenue est un coloriage particulier du réseau, dont les propriétés de connectivité attirent particulièrement l'attention des mathématiciensmathématiciens. Par connectivité, il faut entendre les domaines connexesconnexes, c'est-à-dire les " îles ", comme celles repérées en bleu et en rouge.

Percolation : dans ce réseau en nid d'abeilles, on choisit au hasard de griser ou non chaque cellule.
Crédits : Salvatore Tummarello

Domaines connexes ou " îles ".
Crédits : Salvatore Tummarello
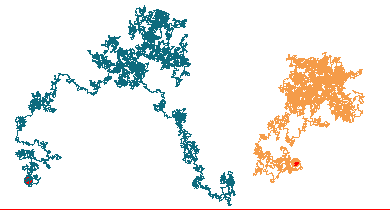
En particulier, il existe toujours (quitte à inverser le blanc et le gris) une île telle que celle coloriée en bleu sur la figure précédente, à savoir un domaine qui joint deux bords opposés du réseau. Encore une fois, un objet limite va apparaître en faisant tendre la taille des cellules vers zéro : le domaine connexe de cet objet limite qui remplit tout le réseau s'appelle un " amas de percolation " (voir ci-dessous). La structure de ces amas de percolation est assurément très complexe, mais W. Werner et son équipe ont néanmoins pu montrer que ces amas vérifient la même propriété que les mouvements browniens : leurs frontières ont pour dimension fractale 4/3.

Percolation et amas de percolation à droite.
Crédits : Salvatore Tummarello
Exposants d'intersection brownien
W. Werner a également résolu une conjecture concernant les calculs d'" exposants d'intersection browniens ". Prenons deux marches aléatoires indépendantes dans le plan issues de deux points distincts au temps t=0 ; les physiciensphysiciens-théoriciens (notamment en mécanique statistique) savaient que la probabilité pour que les deux trajectoires ne se soient pas rencontrées à l'instant t décroît comme une puissance (non-entière) de t. B. Duplantier et K.-H. Kwon ont ainsi prédit en 1988 que cet exposant, dit d'intersection brownien, devait valoir -5/8. W. Werner et ses collaborateurs ont résolu la conjecture, qu'ils ont même généralisée à des nombres quelconques de groupes de mouvements browniens. Ils ont en outre montré que les exposants vérifient des relations remarquables entre eux.
Si deux particules sont animés d'un mouvement brownien, quel est la probabilité pour que leurs trajectoires ne se soient jamais rencontrées ?
Crédits : Salvatore Tummarello
Représentations conformes et processus SLE
Un des instruments fondamentaux dont W. Werner a fait usage porteporte le nom d'analyse complexe. Sans entrer dans trop de détails, l'analyse complexe permet entre autre de caractériser simplement les transformations du plan qui conservent les angles : ces transformations sont dites " conformes ". Comme exemple, la figure ci-dessous illustre l'effet de l'application " exponentielle " sur les coordonnées cartésiennes, qu'elle transforme en coordonnées polaires. Or Paul Lévy a publié en 1947 un théorème expliquant que s'il on applique une transformation conforme à un mouvement brownien, la courbe déformée est encore un mouvement brownien. Par conséquent, ce résultat majeur a permis d'établir des connexions fécondes entre deux branches des mathématiques a priori éloignées, les probabilités et l'analyse complexe.
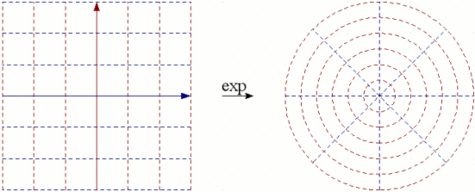
L'application exponentielle envoie les droites verticales sur des cercles et les droites horizontales sur des demi-droites issues de l'origine. L'application exponentielle est conforme : elle conserve les angles.
Crédits : Salvatore Tummarello
Il était bien connu des spécialistes depuis les années 1980 que l'invariance conforme joue un rôle important dans l'analyse des modèles tels que le mouvement brownien. Mais l'outil d'investigation majeur que W. Werner a abondamment étudié est encore un autre type de processus aléatoire, baptisé SLE pour Stochastic (ou Schramm) Loewner Evolution (processus de Schramm-Loewner). Introduit par O. Schramm en 1999, le processus SLE est construit à partir d'une équationéquation due à Loewner (utilisée entre autre par L. de Branges dans sa démonstration de la conjecture de Bieberbach) : il se comporte de manière similaire au mouvement brownien en regard des transformations conformes, et s'avère relativement plus simple à étudier. On peut s'accorder sur le fait que le processus SLE constitue la pierre angulaire de l'œuvre de W. Werner et qu'il lui permettra certainement d'apporter de nouvelles moissons de théorèmes, notamment au sujet des courbes auto-évitantes1...
1. Les courbes auto-évitantes sont construites sur une variante de la marche aléatoire, consistant à ne pas autoriser que la trajectoire se replie sur elle-même.