Les fractales, ces structures géométriques qui se répètent à l’infini, ont de quoi réconcilier tout un chacun avec les mathématiques. Mais elles sont aussi hypnotisantes que complexes. Pour explorer en toute sérénité la dimension fractale, Unisciel et l’université de Lille 1 nous offrent cet épisode de Kézako.

au sommaire

    Les fractales sont des objets mathématiques particulièrement complexes, qui ne s'expliquent pas par la géométrie conventionnelle. Elles présentent une structure invariante par changement d'échelle : on retrouve des détails identiques, ou similaires, quand on zoome à l'infini. Par ailleurs, ces objets ont une dimension fractale, en général non entière.

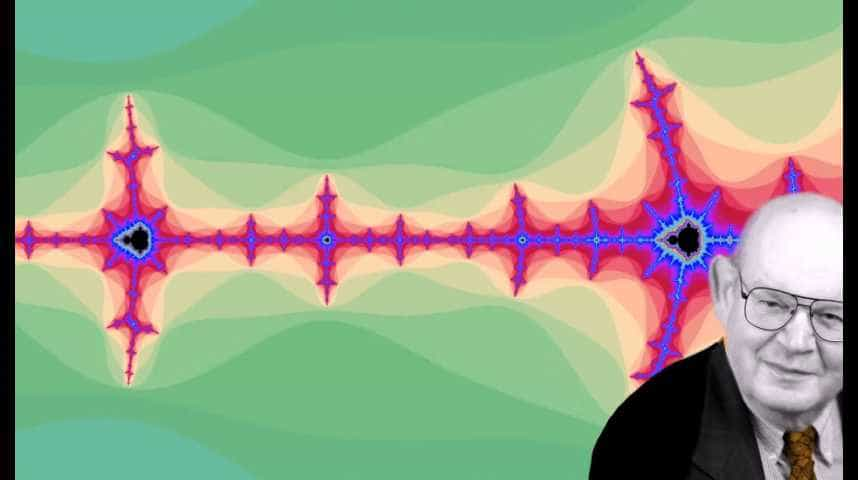
    Le terme « fractal » a été inventé par Benoît MandelbrotBenoît Mandelbrot en 1974. D'où le nom d'ensemble de Mandelbrot, donné à une des fractales les plus connues. Cependant, un mathématicienmathématicien a inventé dès 1904 la courbe de Koch, ou flocon de Koch. Obtenue à partir d'un triangle équilatéral répété à l'infini, cette fractale n'est ni une courbe (dimension 1), ni une surface (dimension 2) : elle est de dimension 1,26. De plus, le périmètre du flocon est infini, tandis que sa surface est finie.

    Les fractales nous aident à comprendre le monde

    Les objets fractals, a priori très abstraits, se manifestent partout dans la nature. Le chou romanesco, les fougèresfougères, les flocons de neige, les poumonspoumons, les vaisseaux sanguins, les littoraux, les éclairséclairs, les lignes de faille, l'ADNADN, n'en sont que quelques exemples. Ils ont donc de nombreuses applications.

    Grâce aux fractales, on peut modéliser des structures complexes, comme les nuagesnuages, les montagnes, ou encore les structures de l'univers. On peut également prévoir la météométéo ou le cours de la bourse. D'autre part, l'art fractal, inventé dans les années 1980 et consistant à générer des fractales hypnotisantes par ordinateurordinateur, contribue certainement à leur popularité.

    © Kézako