Pour les mathématiciensmathématiciens, l'hypothèse posée par l'Allemand Bernhard RiemannBernhard Riemann en 1859 conjecture que les zéros non triviaux -- ou les solutions non triviales -- de la fonction zêta ont une partie réelle égale à ½. Cette hypothèse constitue l'un des problèmes les plus complexes des mathématiques. Vous l'aurez compris, elle représente aussi un concept bien difficile à expliquer aux non-spécialistes. Toujours est-il que des chercheurs de l'université Brunel, à Londres (Royaume-Uni), ont découvert une autre fonction -- un opérateur, plus exactement -- dont les valeurs propres coïncident avec les solutions non triviales de la fonction zêta. Un premier pas vers la résolutionrésolution de l'énigme de l'hypothèse de Riemann.
Avant de poursuivre, précisons que l'hypothèse de Riemann apparaît dans la théorie des nombres et, plus exactement, dans la théorie des nombres premiers. Ainsi, alors qu'il étudiait la distribution de ces nombres un peu particuliers, Bernhard Riemann conjectura que cette distribution, pour des nombres premiers plus petits que N, était liée aux solutions non triviales de cette fonction aujourd'hui connue sous le nom de « fonction zêta ». Il fit alors l'hypothèse que toutes ses solutions non triviales devraient suivre, dans le plan complexe, une ligne d'équation ½ + it et, de fait, présenter une composante réelle toujours égale à ½. Depuis, les mathématiciens ont trouvé des milliards de zéros non triviaux à la fonction zêta et tous présentent effectivement une composante réelle égale à ½. Cependant, l'universalité de la théorie reste toujours à prouver.
Il se trouve que la partie imaginaire t des zéros non triviaux de la fonction zêta constitue un ensemble de nombres réels et discrets, tout comme les valeurs propres de l'opérateur différentiel, un opérateur bien connu des physiciensphysiciens. Alors, les mathématiciens se sont demandé s'il existait un opérateur différentiel dont les valeurs propres correspondraient exactement aux solutions non triviales de la fonction zêta. C'est exactement ce à quoi sont aujourd'hui parvenus les chercheurs de l'université Brunel.
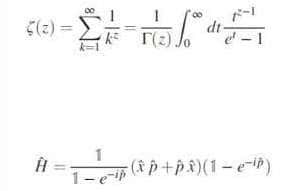
En haut, la fonction zêta de Riemann et en bas, l’opérateur hamiltonien construit par les chercheurs de l’université Brunel. © Université Brunel
La physique vole au secours des mathématiques
Cet opérateur nouvellement découvert présente des liens étroits avec la physique quantique. Deux physiciens, Michael Berry et Jonathan Keating, avaient d'ailleurs déjà avancé, en 1999, l'hypothèse -- qui porteporte aujourd'hui le nom de « conjecture de Berry-Keating » -- qu'un tel opérateur devrait correspondre à un système quantique théorique avec des propriétés particulières. Les travaux des chercheurs britanniques semblent le confirmer. À ceci près que leur opérateur -- un hamiltonienhamiltonien -- ne semble par décrire réellement un système physique, mais plutôt une fonction purement mathématique.
Il reste cependant toujours à prouver que toutes les valeurs propres de cet opérateur sont des nombres réels et non des nombres imaginaires. Dans leurs conclusions, les chercheurs de l'université Brunel semblent confiants à ce sujet. Ils avancent pour cela un argument fort basé sur la symétrie PT. Ce concept de la physique des particules veut que la symétrie des lois de la physique soit respectée pour des transformations impliquant simultanément la parité -- inversion d'espace -- et le temps.
L'opérateur construit par les chercheurs britanniques présente une symétrie PT. Les mathématiciens estiment donc que si cette symétrie peut être brisée pour la partie imaginaire de l'opérateur, il s'en suivra que ses valeurs propres seront toutes des nombres réels. L'hypothèse de Riemann -- sur laquelle repose un certain nombre de principes informatiques et de cryptographiecryptographie, mais aussi quelques principes mathématiques plus fondamentaux -- serait alors enfin prouvée !