au sommaire
Très tôt, dès les premiers partages de jouets ou de friandises, on apprend que certains nombres entiers, tel 6 = 2 x 3, se « cassent » aisément en deux facteurs.
Pour connaître en une seule fois un grand nombre de nombres premiers consécutifs et pas trop grands (par exemple inférieurs à un milliard), on dispose d'une méthode vieille de plus de 2.000 ans.
La décomposition en facteurs premiers
Comme tout nombre entier supérieur à 1 est divisible par au moins un nombre premier, on comprend de façon intuitive que l'on peut ramener tout nombre entier à un produit où ne figurent que des nombres premiers.
L’unicité de la décomposition en facteurs premiers
Ce théorème « clé » est ce qui nous manquait pour prouver enfin le résultat d'unicité de la décomposition en facteurs premiers.
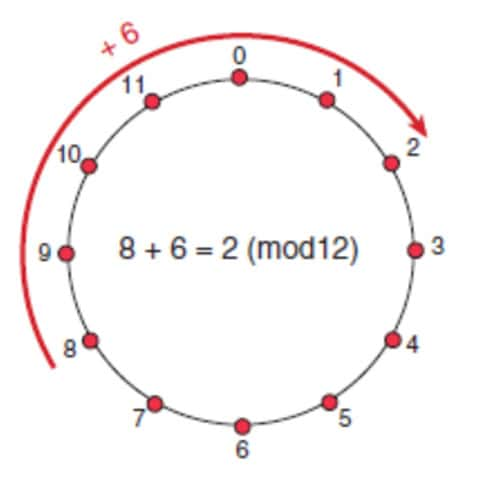
L’arithmétique modulaire et les nombres premiers
Il existe un outil remarquable qui simplifie les raisonnements arithmétiques et facilite la compréhension de bien des propriétés des nombres entiers.
Arithmétique modulaire : le petit théorème de Fermat
En 1640, le mathématicienmathématicien français Pierre de FermatPierre de Fermat énonçait une conjecture (une affirmation mathématique non démontrée) très importante pour notre propos, car elle est à l'origine de nombreux tests de primalité.
L’histoire du plus grand nombre premier et nombres de Mersenne
Il est impossible de dresser la table précise des records du « plus grand nombre premier connu » avant le XVIe siècle : peu de documents des siècles précédents nous sont parvenus.
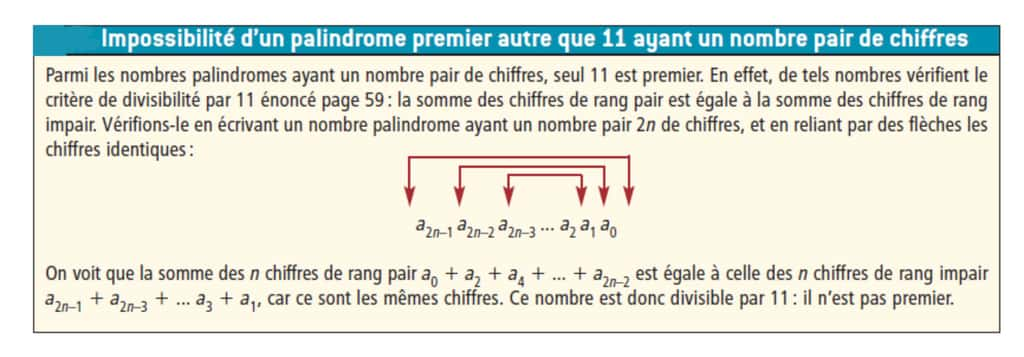
Les nombres premiers palindromes
Le nombre 11 est le seul nombre palindrome à deux chiffres qui soit premier : en effet, un tel nombre est de la forme XX, donc multiple de 11.
Le livre de Jean-Paul Delahaye sur les nombres premiers
À découvrir aux éditions Belin, Merveilleux nombres premiers, voyage au cœur de l'arithmétique, un ouvrage de Jean-Paul DelahayeJean-Paul Delahaye.