Les mathématiciens ont parfois de drôles d'obsessions. Vous l'avez remarqué, vous aussi ? Celle de trouver un motif qui ne se répète jamais est sans aucun doute de celles-là. Pas moins de 50 ans qu'ils cherchaient. Ils l'ont enfin découvert !
au sommaire
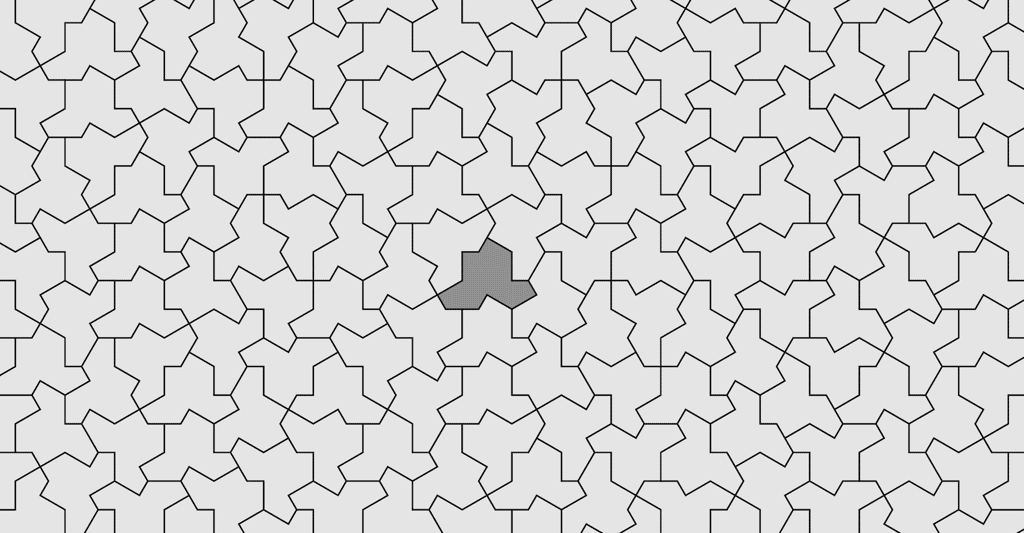
Cela faisait bien 50 ans que les mathématiciens du monde entier étaient sur sa trace. Une forme à nulle autre pareil. Parce qu'elle serait capable de recouvrir une surface, sans laisser d'espace ni faire apparaître de chevauchement, et surtout, sans jamais se répéter. La théorie disait qu'elle existait, quelque part. Mais personne n'avait encore pu mettre la main dessus. Cette fois pourtant, cela semble être chose faite. La forme en question est composée de huit cerfs-volants reliés par leurs bords. Et avec ses 13 côtés, ce polygone ressemble vaguement à un chapeau.
Dans les années 1970, le physicienphysicien Roger Penrose avait proposé un exemple de pavage presque parfait que les chercheurs qualifient d'apériodique. Le célèbre pavage de Penrose. Mais son motif s'appuyait sur deux formes différentes. Cette fois, c'est bien un monotile apériodique que l'équipe internationale réunie derrière un mathématicienmathématicien non professionnel présente. Le tant recherché « einsteineinstein ». Sans lien avec le célèbre physicien tireur de langue. Mais avec la signification allemande de « ein Stein », « une pierre ».
Des chapeaux d’Einstein dans votre salle de bains ?
Les mathématiciens cherchaient une telle forme depuis un demi-siècle maintenant. Certains avaient même fini par penser qu'elle n'existait pas. Ou au moins par imaginer une forme extrêmement complexe. Alors que ce « chapeau » apparaît d'une simplicité désarmante.
Pour prouver le caractère exceptionnel de cette drôle de forme, les chercheurs se sont appuyés sur de puissants ordinateursordinateurs. Mais aussi sur la force de l'esprit humain. Le premier indice trouvé : le fait que les « chapeaux » en question s'organisent en groupes - appelés métatiles - et ensuite, en groupes plus grands - des supertiles - et ainsi de suite. C'est ce que les mathématiciens observent dans tous les pavages apériodiques. Mais la preuve ultime est venue de déformations extrêmes appliquées au « chapeau ».
Ces travaux enthousiasment bien sûr les chercheurs sur le plan théorique. Mais ils pourraient aussi trouver des applications pratiques dans le domaine des quasi-cristaux, des motifs que l'on retrouve des robotsrobots type Terminator jusqu'aux Kleenex. Et si le cœur vous en dit, il est peut-être temps de donner une allure folle à votre salle de bains et revoyant son carrelagecarrelage...