au sommaire
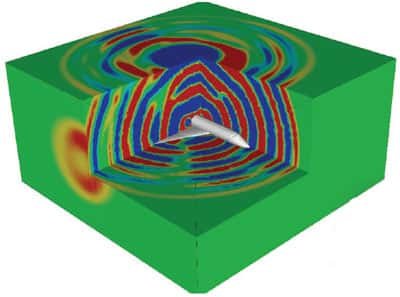
En 3D, le schéma de la réflexion et de la diffraction d'une source acoustique par un avion, obtenu par la méthode Galerkine discontinue appliquée aux équations d'Euler linéarisées. Le Siècle des lumières est toujours avec nous. © Onera
Tout a commencé en Suisse quand Paul et Marguerite Euler confièrent l'éducation mathématique de leur fils Leonhard à un ami de la famille, Jean Bernoulli, frère de Jacques comme chacun sait. Jean et Jacques (qui venait de décéder) étaient de brillants mathématiciensmathématiciens, déjà célèbres. Le petit Leonhard se met ainsi très tôt à se passionner pour le calcul infinitésimal, et montre un talent de surdoué.
Il exercera ses talents à Saint-Pétersbourg puis à Berlin auprès de Frédéric II de Prusse, féru de sciences et de philosophie. Au fil des 886 ouvrages qu'on lui connaît, Leonhard EulerLeonhard Euler traitera de mathématiques, de logique, d'astronomie, d'optique et de mécanique des fluides. Il précisera la notion de fonction, s'attaquera aux nombres complexes, étudiera les orbites des planètes, travaillera sur la nature ondulatoire de la lumière, gambadera dans les champs magnétiques, explorera la théorie des graphes, reliera la trigonométrie aux logarithmes et aux exponentielles, s'amusera avec les équations différentielles et résoudra l'énigme des ponts de Königsberg.
Il reste de lui - entre autres - le cercle d'Euler, l'équation d'Euler, la constante d'Euler, la formule d'Euler, l'identité d'Euler, l'indicateur d'Euler et la méthode d'Euler.
Des collégiens aux ingénieurs, à peu près tout le monde a, un jour ou l'autre, utilisé une notation, un symbole, une équation ou une notion née du cerveaucerveau de ce génie suisse du Siècle des lumièreslumières.

Le début de l'éloge prononcé devant l'Académie des sciences de Paris par le marquis de Condorcet après la mort d'Euler, survenue le 18 septembre 1783. © Académie des sciences
Vous avez déjà croisé Euler…
- y = f(x) : cette notation a été inventée par Euler ;
- i comme imaginaire : pour désigner la racine carrée de -1 (déjà connue), Euler écrit « i » alors qu'il a 20 ans ;
- e est la base des logarithmes naturels (ou népériens) que Leibniz, son découvreur, note « b ». Euler préfère « e » ;
- e est un nombre irrationnelnombre irrationnel. Euler l'a démontré ;
- eix = cos(x) + i sin(x) : ou comment la trigonométrie rejoint l'analyse ;
- eiπ + 1 = 0 : cette magnifique identité remarquable (« l'identité d'Euler ») liera ensemble pour toujours le nombre Pi, la base e des logarithmes naturels et le nombre imaginaire i, alors qu'ils appartenaient jusqu'ici à des domaines distincts ;
- S - A + F = 2 : cette formule est vraie pour tout polyèdre à S sommets, A arrêtes et F faces ;
- En mécanique des fluides, l'équation d’Euler caractérise l'écoulement, avec vitessevitesse et pressionpression, d'un fluide parfait. Aucun ne l'est mais, en pratique, de l'airair à grande vitesse s'en approche. Euler a servi l'aéronautique...
- En résistancerésistance des matériaux, on enseigne la théorie d'Euler-Bernoulli qui décrit les contraintes dans une poutrepoutre à l'aide d'équations différentielles. La tour Eiffel lui doit beaucoup.























