Comment décrire les mouvements de la Lune sous l'action du Soleil et de la Terre dans le cadre de la théorie de Newton de la gravitation et des lois de la mécanique céleste qui en découle ? C'est un exemple particulier de ce que l'on appelle le « problème à trois corps » dont l'étude a reçu les contributions de mathématiciens de premier calibre depuis des siècles, à commencer par Newton lui-même. On dit souvent qu'il n'a pas de solution générale, mais ce n'est pas vrai. Alors que l'adaptation du roman de Liu Cixin du même nom est un succès sur Netflix, c'est une bonne occasion de faire plus ample connaissance avec ce problème légendaire.
au sommaire
Cela fait presque un mois que Netflix a commencé à diffuser l'adaptation du célèbre roman écrit par l’écrivain chinois Liu Cixin et dont le titre est Le Problème à trois corps, premier tome d'une trilogie, également composée de La Forêt sombre et La Mort immortelle. L'ouvrage a été lauréat du prix Hugo en 2015. Rappelons que ce prix récompense des romans de science-fiction ou de fantasy publiés pendant l'année calendaire précédente. Arthur Clarke a été de nombreuses fois lauréat et tout comme dans son cas, l'ouvrage de Liu CixinLiu Cixin entre dans la catégorie dite de « hard science-fiction », c'est-à-dire que l'on essaye le plus possible de rendre l'histoire compatible avec la physique connue ou encore spéculative mais sur des bases scientifiques. C'est le cas par exemple d'Interstellar.
À cet égard, on peut se demander ce que signifie déjà tout simplement le titre du roman de Liu Cixin et à quoi il fait référence.
Le « problème à trois corps » est un célèbre problème mathématique en mécanique céleste. Il s'agit de trouver toutes les solutions mathématiques possibles des équations différentielles décrivant les mouvements de trois astres s'attirant les uns les autres sous l'effet de la gravitation.
Rappelons que NewtonNewton fut le premier à trouver puis intégrer, c'est-à-dire résoudre les équations différentielles décrivant les mouvements de deux corps en mécanique céleste. Il lui a fallu pour cela découvrir la loi de la gravitation, le calcul infinitésimal et enfin poser les bases de la théorie des équations différentielles (une des meilleures introductions à ces sujets mathématiques se trouve dans le traité d'analyse de Richard Courant). Par la suite, on a rapidement cherché à décrire les mouvements combinés de trois corps bien connus : la Terre, le SoleilSoleil et la LuneLune. Le pas suivant a été tout naturellement de tenter de rendre compte autant que possible de tous les mouvements de tous les corps du Système solaireSystème solaire, planètes, comètescomètes et astéroïdesastéroïdes compris en interaction gravitationnelle.
Orbites à trois corps et plus : le Système solaire est-il stable ?
Déjà au XVIIIe siècle, les mathématiciensmathématiciens Jean d'Alembert et Alexis Clairaut s'étaient particulièrement penchés sur cette problématique du mouvement des planètes, ce qui les avait conduits à parler justement de ce casse-tête mathématique en les termes de « problème à trois corps ». Se posa alors avec plus d'intensité la question, déjà perçue par Newton, de la stabilité à long terme des orbitesorbites avec trois et même N corps en mécanique céleste. Il n'était pas impossible que les orbites bien régulières du Système solaire ne soient qu'une phase transitoire de celui-ci, quand bien même cette transition pouvait durer des milliards d'années.
Toujours est-il qu'une première famille de solutions particulières exactes du problème à trois corps a été découverte par Euler et Lagrange à la fin du XVIIIe siècle et qui fait intervenir les fameux points de Lagrangepoints de Lagrange. Or, pour des cas plus généraux, force était de considérer les équations de mouvement du problème à deux corps, tout en y incluant des termes supplémentaires traduisant l'existence de petites forces perturbatrices. C'est dans ce contexte que se développa la théorie des perturbations en mécanique céleste avec Joseph-Louis LagrangeJoseph-Louis Lagrange, Pierre-Simon LaplacePierre-Simon Laplace mais aussi Carl Friedrich Gauss.
En 1889, le roi Oskar II de Suède, souhaitant fêter son anniversaire, créa sur la proposition du mathématicien Gösta Mittag-Leffler un prix pour récompenser le meilleur mémoire sur le problème à N corps. Le problème fut posé en ces termes, par le grand mathématicien allemand Karl Weierstrass : « Étant donné un système de N corps qui s'attirent mutuellement conformément à la loi de la gravitation, et en supposant qu'il n'y ait jamais de collision entre deux corps, donner les coordonnées des corps individuels, pour n'importe quel moment de l'avenir ou du passé, sous la forme d'une série uniformément convergente dont les termes sont composés de fonctions connues ».

Un problème à N corps intégrable ?
C'est le physicienphysicien et mathématicien Henri Poincaré qui remporta ce prix en révolutionnant les méthodes de la mécanique céleste... mais en répondant en quelque sorte à la question posée par la négative. Ce faisant, il a entrevu la théorie du chaos et a posé les fondements de la théorie moderne des systèmes dynamiques dans le célèbre traité Les méthodes nouvelles de la mécanique céleste.
Souvent, on affirme que les résultats de Poincaré prouvent qu'il n'est pas possible d'intégrer, c'est-à-dire de résoudre analytiquement les équations différentielles du problème à trois corps pour aboutir à une solution générale. La réalité est plus nuancée, et l'on pourrait même dire que cette affirmation est fausse.
Mais comme le mentionne le mathématicien Alain Chenciner de l'Institut de mécanique céleste et de calcul des éphémérides (IMCCE) dans un article de Scholarpedia : « Bien que le problème à deux corps soit complètement intégrable et ses solutions parfaitement comprises, il n'en est pas de même avec les solutions du problème à trois corps, qui peuvent être d'une complexité arbitraire et sont très loin d'être entièrement comprises. »
En fait, ce que Poincaré a démontré, c'est qu'en supposant certaines conditions assez raisonnables pour l'expression analytique de la solution générale du problème à trois corps, celle-ci n'existait pas.
Toutefois, en posant moins de conditions comme hypothèse de départ, dès le début du XXe siècle, le mathématicien Karl Frithiof Sundman a effectivement trouvé une solution très générale et, en 1991, un autre mathématicien, Qiudong Wang, a même trouvé une solution générale au problème à N corps.
On parle rarement de ces solutions parce qu'elles sont inutilisables en pratique pour faire des calculs. Il faut calculer des sommes qui convergent extrêmement lentement vers la solution comme l'explique la vidéo ci-dessous (même pour des distances et des temps courts).
Une présentation du problème à trois corps et ses solutions. Pour obtenir une traduction en français assez fidèle, cliquez sur le rectangle blanc en bas à droite. Les sous-titres en anglais devraient alors apparaître. Cliquez ensuite sur l'écrou à droite du rectangle, puis sur « Sous-titres » et enfin sur « Traduire automatiquement ». Choisissez « Français ». © PBS Space Time
De nouvelles familles de solutions périodiques
S'il n'est pas possible de vraiment trouver une solution générale au problème à trois corps calculable en pratique, il est possible de trouver des familles de solutions particulières qui le sont. Après celles d'Euler et Lagrange, les mathématiciens Roger Broucke et Michel Hénon ont trouvé dans les années 1970 leur solution particulière éponyme. En 1993, le physicien Cristopher Moore du Santa Fe Institute en a dévoilé une autre, qui intègre des orbites en forme de huit.
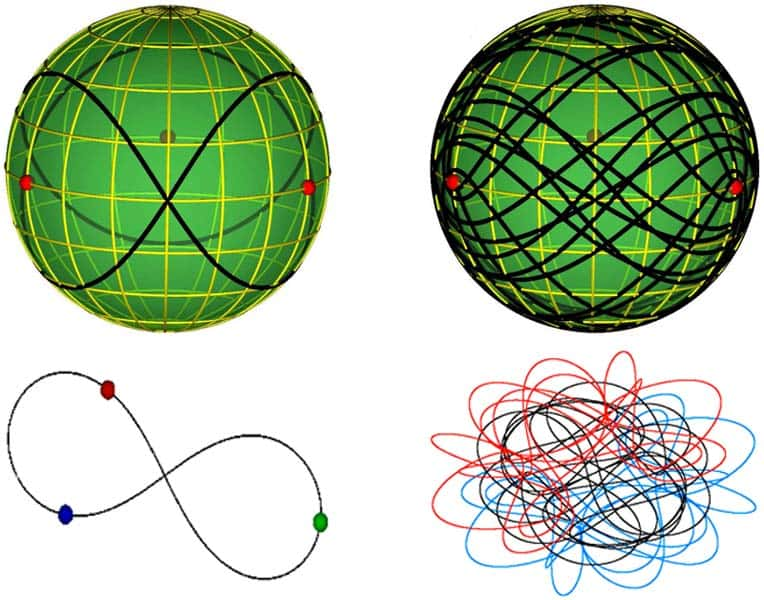
Il y a quelques années, deux physiciens serbes de l'Institut de physique de Belgrade, Milovan Suvakov et Veljko Dmitrasinovic, ont créé la surprise en publiant sur arxiv un article dans lequel ils annonçaient avoir découvert et classifié 13 nouvelles familles de solutions, à l'aide d'un ordinateurordinateur.
Sphère à trois trous et courbes en lacets
Ils ont commencé par considérer un problème à trois corps restreint avec des orbites périodiques dans le plan, des massesmasses égales et un moment cinétiquemoment cinétique total nul. Inspirés par les travaux de Cristopher Moore, Chenciner et Montgomery sur les orbites en forme de huit, ils ont réalisé des simulations numériquessimulations numériques avec différentes conditions initiales.
Les trajectoires complexes des trois corps dans le cas considéré peuvent alors se mettre en correspondance avec des courbes en lacets à la surface d'une sphère avec trois trous. Ces courbes peuvent alors être classées avec des méthodes topologiques et algébriques, ce qui permet du même coup de classifier ces orbites. Selon les physiciens serbes, si ces solutions restent stables quand on les perturbe un peu (en particulier en considérant des masses différentes), il n'est pas impossible qu'elles décrivent ce qui se passe dans certains systèmes d'exoplanètes.

Quelques rappels concernant des solutions numériques à des équations différentielles. Il existe de longue date des méthodes pour calculer des approximations aux solutions de ces équations sans connaître la forme analytique de ces solutions, c'est-à-dire des combinaisons de fonctions élémentaires finies, fussent-elles des sommes de polynômespolynômes simples ou de fonctions trigonométriques. Il n'est pas difficile de calculer des solutions numériques pour les mouvements d'une dizaine de planètes considérées comme des points matériels avec un ordinateur personnel de la fin des années 1980 par exemple.
On peut s'en convaincre en parcourant l'un des chapitres du célèbre cours de physique de Feynman pour des étudiants de première année à l'université. Sur une courte échelle de temps, on peut donc en pratique obtenir des solutions approchées des mouvements de plusieurs corps et de fait, c'est ce que l'on fait pour le Système solaire et le suivi des sondes interplanétaires. Ainsi, une sonde lunaire doit tenir compte de l'attraction du Soleil, de la Terre et de la Lune, ce qui revient à résoudre numériquement un problème à quatre corps.
Chaos et climat avec 3 corps
Pour terminer et en revenir un peu au roman de Cixin Liu, voici ce qu'en dit dans un communiqué de l’université de Virginia Tech aux États-Unis, Shane Ross, Professeur d'ingénierie aérospatiale et océanique qui a apporté une contribution fondamentale à la recherche de solutions chaotiques au problème à trois corps.
« Il n'existe aucune configuration connue de trois étoilesétoiles massives qui pourraient maintenir une orbite erratique. Il y a environ 20 ans, il y a eu une grande avancée lorsqu'une solution en forme de huit a été découverte pour résoudre le problème des trois corps, dans laquelle trois étoiles de taille égale se poursuivent sur une trajectoire en forme de huit. En fait, Cixin Liu y fait référence dans ses livres. S'appuyant sur cette évolution, d'autres mathématiciens ont trouvé d'autres solutions, mais dans chaque cas, le mouvement n'est pas chaotique. »
Et il ajoute : « Il est encore plus improbable qu'un quatrième corps, une planète, soit en orbite autour de ce système de trois étoiles, même de manière erratique : soit elle entrerait en collision avec une autre, soit elle serait éjectée du système. La situation dans le livre serait donc une solution au « problème des quatre corps », qui, je suppose, n'avait pas tout à fait la bonne sonorité pour être utilisé comme titre.
De plus, un climatclimat stable est peu probable, même sur une planète semblable à la Terre. Au dernier décompte, il existe au moins une centaine de facteurs indépendants qui sont nécessaires pour créer une planète semblable à la Terre qui abrite la vie telle que nous la connaissons. Nous avons eu la chance d'avoir connu pendant environ 10 000 ans le climat le plus stable de l'histoire de la Terre, ce qui nous fait penser que la stabilité climatique est la norme, alors qu'en fait, c'est l'exception. Ce n'est probablement pas une coïncidence si cela correspond à l'essor d'une civilisation humaine avancée ».