Les détecteurs d'ondes gravitationnelles, comme Ligo ou Virgo, ne pourraient pas atteindre leur but s'ils n'étaient pas capables de mesurer l’étirement et la compression du tissu de l’espace-temps à des échelles 10 000 milliards de milliards de fois plus petites qu’un cheveu humain. Tout comme la mécanique quantique limite la précision des mesures de la position et de la vitesse des électrons, elle limite la mesure des ondes gravitationnelles avec des faisceaux laser. Mais les physiciens savent comment tirer parti au maximum de ses limites et ils viennent de battre un nouveau record à ce sujet, ce qui va faire progresser l'astronomie gravitationnelle.
au sommaire
C'est assez incroyable quand on y pense. À la fin de l'année 1915, Albert EinsteinEinstein publie la forme finale de sa théorie de la relativité générale et aux cours des trois années qui vont suivre il va en tirer des réflexions et des équations concernant les ondes gravitationnellesondes gravitationnelles rassemblées dans un article de 1918. En effet, son espace-temps courbe est dynamique et se comporte comme un milieu matériel élastique dans lequel des équivalents des ondes sonores peuvent se propager. Il aboutit également à des équations rappelant celles des ondes électromagnétiques.
En fait, un débat sur l'existence réelle de ces ondes va s'engager dans les décennies suivantes et il faudra attendre la fin des années 1950 avec notamment un argument de Richard Feynman, pour que ce débat prenne fin (la vérité historique est plus complexe que cela, comme l'ont expliqué dans leur ouvrage Nathalie Deruelle et Jean-Pierre Lasota).
Einstein ne pensait initialement sans doute pas que l'on puisse un jour détecter directement ces ondes sur Terre car elles sont vraiment très faibles et il faut des objets très massifs en mouvement accélérés pour les produire significativement. Mais entre 1915 et 1918, après sa découverte de la relativité généralerelativité générale, Einstein a sans doute plus de temps pour revenir sur la problématique des quanta de lumièrelumière et en 1917, cherchant à retrouver la loi du corps noircorps noir concernant l'émissionémission des corps chauffés, comme dans le cas d'un filament d'ampoule électrique, à partir de la théorie de l'atome de Bohratome de Bohr, il tombe sur les principes de l'effet laserlaser.
Or, c'est précisément la clé qui va permettre de détecter les ondes gravitationnelles avec les détecteurs LigoLigo et VirgoVirgo à partir de 2015. De façon stupéfiante, Einstein a donc découvert à la fois un effet fondamental de la relativité générale et un effet fondamental de la mécanique quantiquemécanique quantique pour détecter et mesurer le premier.
Ligo et Virgo, des interféromètres de Fabry-Perot avec des lasers
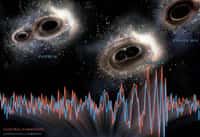
Le principe utilisé pour Ligo aux États-Unis et Virgo en Europe est simple, il faut commencer par faire circuler des faisceaux laser en les faisant rebondir sur des miroirsmiroirs dans deux tubes sous vide orthogonaux longs de plusieurs kilomètres. Au passage d'une onde gravitationnelle souvent émise à des dizaines ou centaines de millions d'années-lumièreannées-lumière par des collisions de trous noirs stellairestrous noirs stellaires ou d'étoiles à neutronsétoiles à neutrons, les distances spatiales varient sur Terre de seulement 1/10 000e de la largeur d'un protonproton ! Toutefois, en empruntant deux chemins différents avec les deux tubes avant d'être combinés, des faisceaux laser vont être décalés l'un par rapport à l'autre par cette variation de distance, de sorte qu'ils vont interférer comme l'explique la vidéo ci-dessus. On obtient alors des franges d'interférenceinterférence.
Comme on l'a dit, il faut pouvoir détecter une variation de distance incroyablement petite, ce qui veut dire qu'il faut pouvoir faire des mesures d'une incroyable finesse et peu bruitées. On a donc construit deux détecteurs basés sur le principe d'un interféromètreinterféromètre de Fabry-Perot séparés par des milliers de kilomètres aux États-Unis avec Virgo, de façon qu'une perturbation locale, comme un petit séismeséisme, soit facilement détectable puisqu'elle se produirait plus fortement dans un détecteur que dans un autre et qu'il devient alors possible de soustraire des signaux enregistrés ce bruit, pour remonter au signal des ondes gravitationnelles.
Le professeur Lee McCuller, professeur adjoint de physique à Caltech, décrit une nouvelle technologie de pointe, appelée compression quantique dépendant de la fréquence, qui renforce la capacité du Ligo à effectuer des mesures ultra-précises. La compression quantique dépendante de la fréquence est analogue à la compression du ballon dans les deux sens et améliore la précision du Ligo sur la gamme d'ondes gravitationnelles qu'il détecte. Pour obtenir une traduction en français assez fidèle, cliquez sur le rectangle blanc en bas à droite. Les sous-titres en anglais devraient alors apparaître. Cliquez ensuite sur l'écrou à droite du rectangle, puis sur « Sous-titres » et enfin sur « Traduire automatiquement ». Choisissez « Français ». © Caltech, R. Hurt (IPAC)
Toutefois, la mécanique quantique, qui permet l'effet laser et donc de faire des mesures spectaculaires d'une grande précision comme le montre l'attribution du prix Nobel de physique 2023 avec les lasers attosecondes, produit aussi ses propres limites et bruits quantiques via notamment le fameux principe d'incertitude de Heisenbergprincipe d'incertitude de Heisenberg que les physiciensphysiciens rigoureux préfèrent appeler entre eux les inégalités de Heisenberginégalités de Heisenberg.
Les membres de la collaboration Ligo viennent cependant de faire savoir via un article publié dans Physical Review X qu'ils avaient repoussé les limites quantiques précédentes en utilisant la technique des états compressés de la lumière, squeezed light en anglais. L'idée est ancienne car on savait déjà dès le début des années 1970 que la détection des ondes gravitationnelles nécessiterait dans les instruments de tenir compte des effets quantiques, comme l'avaient montré les travaux du regretté physicien russe Vladimir Braginsky sur la théorie des mesures quantiques (voir son livre Quantum Measurement).
En fait, on utilise des états comprimés de la lumière avec Ligo depuis 2019, mais c'est une variante, avec des états comprimés différemment selon les fréquencesfréquences des ondes laser utilisées, qui vient finalement d'être mise en pratique avec succès.
La lumière comprimée et les inégalités de Heisenberg
Comme il est expliqué plus en détail dans la partie de l'article en piste noire et son complément dans la vidéo ci-dessous, on a une inégalité de Heisenberg saturée de la forme ΔAΔφ= ħ (où ħ est la constante de Planckconstante de Planck) pour une onde monochromatique pure avec une seule fréquence. Les incertitudes ΔA et Δφ sont comme les valeurs des axes d'une ellipse et donc forment un cercle si elles sont égales dans un plan avec des axes A et φ formant ce que l'on appelle un espace de phase ou encore de configuration. On peut donc obtenir une ellipse avec un ΔA grand pour un Δφ petit et inversement pourvu que ΔAΔφ= ħ reste toujours vraie.
L'idée centrale est de comprimer l'ellipse différemment selon que l'on mesure des fréquences hautes ou basses dans le signal des ondes gravitationnelles avec un spectrespectre d'impulsion laser contenant plusieurs fréquences pour cela.
Dans l'état actuel, car bien sûr les progrès vont se poursuivre, la nouvelle sensibilité des détecteurs de Ligo va permettre de détecter environ 60 % de fusionsfusions de trous noirs stellaires et d'étoiles à neutrons de plus dans le volumevolume que peuvent sonder les deux machines. Rappelons que ces fusions sont rares dans une vie d'homme, de sorte qu'il faut pouvoir sonder un volume de grande taille pour avoir assez de sources détectables sur quelques mois seulement d'observation au moins.
La mécanique quantique nous interdit de mesurer l’univers au-delà d’un certain niveau de précision. Mais cela ne nous empêche pas d’essayer de nous rapprocher le plus possible de cette limite pour mesurer et détecter les ondes gravitationnelles en utilisant la lumière comprimée comme l’explique cette vidéo. Pour obtenir une traduction en français assez fidèle, cliquez sur le rectangle blanc en bas à droite. Les sous-titres en anglais devraient alors apparaître. Cliquez ensuite sur l'écrou à droite du rectangle, puis sur « Sous-titres » et enfin sur « Traduire automatiquement ». Choisissez « Français ». © PBS Space Time
Pour les courageux, après des explications de niveau piste verte, voici des explications de niveau piste noire.
La lumière comprimée est un sujet fascinant pour les physiciens car elle permet d'étudier les fluctuations quantiques au cœur de la théorie des champs. Ce que l'on appelle les états quantiques comprimés se retrouve même dans la description du rayonnement des trous noirs.
L'intérêt des sources de lumière comprimée n'est pas que théorique. Les fluctuations quantiques de la lumière dans certains dispositifs de mesures fines, et surtout dans les fibres optiquesfibres optiques utilisées pour les télécommunications, peuvent être des causes de perturbations gênantes, dégradant le signal que l'on veut mesurer ou l'information que l'on veut transmettre. C'est pourquoi les moyens d'obtenir des états comprimés de la lumière sont étudiés depuis longtemps.
Qu’est-ce qu’un état quantique comprimé ?
Pour le comprendre, il suffit de considérer le mouvement oscillatoire d'un électronélectron créant une onde électromagnétique. La position x(t) d'un tel électron est donnée de façon simple par la relation suivante :
x(t) = A cos (ωt+φ)
où A est l'amplitude de l'oscillation, ω sa pulsation et φ sa phase. De même, l'onde électromagnétique émise par un tel oscillateur mettra en mouvement un autre électron de la même façon en un point de l'espace et c'est ainsi que l'on définit et mesure l'existence d'un champ électromagnétiquechamp électromagnétique dans l'espace et le temps.
Une modification de cette image simple apparaît lorsque l'on veut tenir compte du fait que les électrons et la lumière ne sont en fait pas des objets classiques mais bien quantiques. La position q et la quantité de mouvementquantité de mouvement p de l'électron (ces quantités sont dites « conjuguées » en mécanique analytique) doivent, si l'on veut continuer à employer une image classique, être limitées par le flou quantique des inégalités de Heisenberg :
ΔqΔp ≥ ħ
Cela se traduit par un flou correspondant de l'amplitude A et de la phase φ dont les fluctuations de valeur ΔA et Δφ doivent vérifier une inégalité similaire à la précédente, bien connue, pour la position et la quantité de mouvement d'une particule.
ΔAΔφ ≥ ħ
On obtient alors la situation décrite par les schémas ci-dessous :
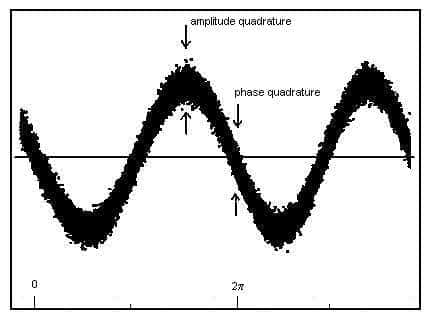
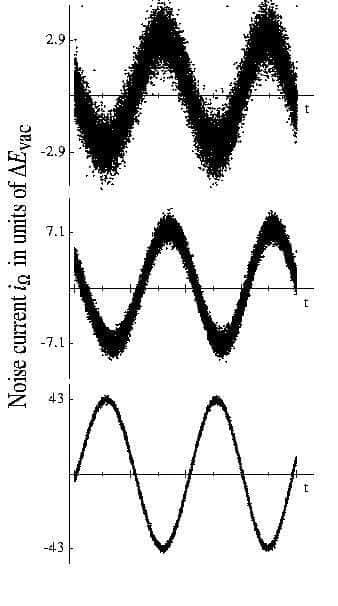
Le mouvement sinusoïdal pur est modifié et il peut se voir comme affecté de fluctuation incessante de la valeur de l'amplitude et de la phase, le mouvement « réel » étant quelque part dans la zone sombre.
Plus l'amplitude de l'oscillation est grande, plus l'effet relatif des fluctuations quantiques est faible et plus l'oscillation se rapprochera d'une description classique du mouvement, avec des valeurs précises de la position q et de la quantité de mouvement p.
Un état comprimé pour une particule est alors défini par deux choses :
- les inégalités se transforment en égalités ;
- il est possible de faire baisser à volonté la dispersion sur l'une des coordonnées conjuguées dans une inégalité de Heisenberg.
On peut donc « comprimer » les fluctuations quantiques pour atteindre le maximum de précision autorisée par les lois quantiques en réduisant donc le « bruit quantique moyen ».
Par exemple, l'amplitude A d'une onde électromagnétique est reliée à la probabilité de trouver un nombre donné de photonsphotons par unité de temps en un point de l'espace. Si l'incertitude sur le nombre de photons présents est de 20 photons/s alors que l'effet fin que l'on cherche à mesurer exige une précision meilleure que 5 photons/s, clairement on a un problème.
La recherche d'états comprimés est précisément le moyen d'avoir un contrôle sur cette incertitude lors de mesures fines.