Interview : Jean-Pierre Luminet explique le modèle de l'univers fini

Futura-Sciences : Le modèle cosmologique dodécaédrique de Poincaré (Poincaré Dodecahedral Space, PDS) possède des caractéristiques distinctes du modèle de concordance [version actuelle du modèle standard, communément acceptée aujourd'hui, NDLRNDLR]. Pouvez-vous nous rappeler brièvement lesquelles ?

Jean-Pierre LuminetJean-Pierre Luminet : Le modèle de concordance actuellement considéré par beaucoup de cosmologistes est un modèle à la topologie simple, comme une sphère. Mais surtout, il est plat et infini. Celui du PDS est un modèle clos, construit à partir d'une géométrie sphérique, mais à la topologie compliquée comme un pneupneu ou un bretzel. Il est donc fini, mais contrairement à un tore plat, il est caractérisé par une courbure positive.

En outre, il conduit à des prédictions concernant sa taille qui sont en principe testables, ce qui n'est pas le cas des modèles cosmologiques infinis. L'une de ces prédictions concerne les observations que l'on peut faire dans le spectre de puissance du rayonnement fossile. Comme la taille de l'univers est finie et inférieure à l'horizon dans le cas du modèle PDS, on doit s'attendre à une coupure pour la taille des longueurs d'onde présentes dans le spectre des fluctuations du rayonnement fossile. C'est facile à comprendre, car des longueurs d'onde plus grandes que la taille de l'univers sont évidemment exclues.

Lorsque l'on mesure, dans toutes les directions de l'espace, l'intensité du rayonnement fossile, et que l'on effectue une sorte de moyenne, on trouve une courbe avec des pics et des oscillations : il s'agit de la fameuse courbe de puissance moyenne montrant l'amplitude de ses fluctuations de températures selon les échelles angulaires et qui dépend donc de l'échelle de résolutionrésolution angulaire avec laquelle on analyse le rayonnement fossile.

Le spectre de cette courbe est une sorte de carte d'identité d'un univers de forme et composition donnée, de même que le spectre d'un atomeatome ou d'une moléculemolécule peut servir à l'identifier. Après la publication des données de WMap, c'est bien à ce niveau-là que vous avez trouvé les premiers indices en faveur du modèle PDS que vous avez étudié avec vos collègues depuis quelques années ?

Jean-Pierre Luminet : Tout à fait ! Au début de la courbe du spectre de puissance du rayonnement fossile, on constatait en 2003 que deux modes, dits quadripolaires et octopolaires, étaient moins présents que prévu dans le cadre du modèle de concordance. Or, c'est précisément le genre de choses auquel on doit s'attendre avec un univers de taille finie, plus petit que l'horizon cosmologiquehorizon cosmologique. Cela correspond à l'absence des grandes longueurs d'onde dont j'ai parlé précédemment.

Le raffinement des mesures de WMap, au bout de trois années d'observations, a fait disparaître le désaccord entre la mesure du mode octopolaire et les prédictions du modèle de concordance, mais le problème persiste toujours avec le mode quadripolaire : c'est un argument sérieux en faveur de notre modèle.

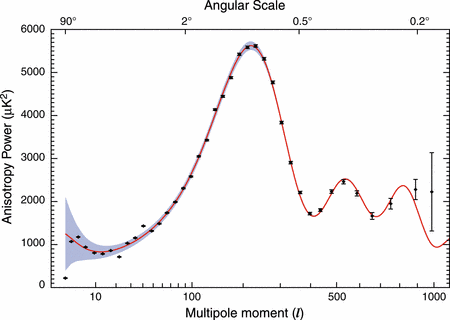
Figure 1. La courbe du spectre de puissance du rayonnement fossile. En rouge, la prédiction du modèle de concordance. La croix en bas à gauche est conforme au modèle PDS et c'est un résultat observationnel. © Nasa

Avec vos collègues (S. Caillerie, M. Lachièze-Rey, R. Lehoucq, A. Riazuelo, et J. Weeks), vous présentez votre modèle cosmologique comme une alternative au modèle de concordance, en particulier parce que vous pouvez être en meilleur accord avec le spectre de puissance du rayonnement fossile fourni par WMap que celui-ci. Toutefois, d'autres observations, comme les supernovaesupernovae et les collisions entre amas de galaxiesamas de galaxies, indiquent la présence d'énergie noireénergie noire et de matière noirematière noire. Cela est-il là aussi compatible avec votre théorie ?

Jean-Pierre Luminet : Nous avons évidemment étudié la question et, non seulement notre modèle incorpore la matière noire et l'énergie noire, mais il le fait avec des proportions identiques à celles du modèle de concordance. Il y a donc compatibilitécompatibilité avec les autres contraintes observationnelles que vous mentionnez.

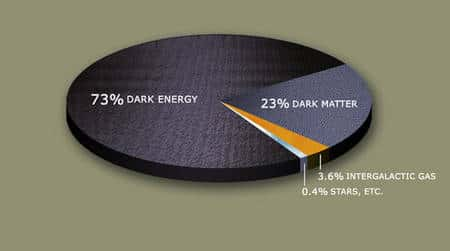
Figure 2. Les proportions d'énergie noire (dark energy) et de matière noire (dark matter) dans l'univers. Le reste est de la matière baryonique normale. © planetquest.jpl.nasa.gov

Le modèle dodécaédrique de Poincaré possède une topologie rigide, cela veut-il dire qu'il fixe la densité totale de l'univers ?

Jean-Pierre Luminet : Non, la densité de 1,018 que nous avons obtenue est celle qui permet l'ajustement le plus précis avec les données de WMap. Néanmoins, comme je vous l'ai dit, le PDS exige une courbure positive pour l'Univers. Cela signifie que la densité totale doit bien être supérieure à 1, sans quoi notre modèle serait réfuté par les observations.

Dans votre cours de cosmologiecosmologie [téléchargeable en fichier PPS, NDLR], vous parlez d'une autre contrainte sur la densité totale dans le modèle PDS : elle ne doit pas être inférieure à 1,009. Si cela était le cas, comme la future mission PlanckPlanck le révélera peut-être, le PDS serait-il là aussi réfuté ?

Jean-Pierre Luminet : À strictement parler, non. En fait, il existe un intervalle de valeurs, pour la densité totale, qui correspond à des Univers dodécaédriques dans lesquels leur taille est plus petite que l'horizon. Dans ce cas, il est possible de savoir si nous sommes dans un Univers décrit par le modèle PDS. Dans le cas contraire, pour des valeurs en dehors de cet intervalle, notre Univers pourrait toujours être décrit par le modèle PDS, mais sa taille serait supérieure à son horizon, et nous ne pourrions donc pas le départager d'autres modèles d'univers, comme le modèle de concordance Lambda CDM.

Le PDS est clos, avec une densité supérieure à la densité critiquedensité critique. Cela veut-il dire que son destin est de finir dans un Big CrunchBig Crunch ?

Jean-Pierre Luminet : Pour autant que nous le sachions, non, car l'énergie noire l'accélère exactement comme dans le cas du modèle de concordance. Il devrait donc continuer son expansion pour l'éternité.

FS : Andrei Linde et sa femme Renata Kallosh ont tout de même proposé récemment que la valeur de la constante cosmologiqueconstante cosmologique puisse changer dans le futur. En utilisant certains modèles de supergravitésupergravité, ils montrent que, même si l'univers est plat, il pourrait néanmoins changer de régime d'expansion dans un futur assez proche, quelques dizaines de milliards d'années, et s'effondrer pour donner un Big Crunch. Pensez-vous qu'une telle chose soit transposable au modèle PDS ?

Jean-Pierre Luminet : Cela me semble tout à fait possible. En fait, la dynamique temporelle [document téléchargeable en PPS, NDLR] (c'est-à-dire le fait que l'univers soit en expansion perpétuelle ou en expansion-contraction par exemple) est totalement découplée du problème topologique de la forme de l'espace.

De prime abord, l'idée d'un espace aux formes polyédriques semble assez surprenante et sans véritable justification. Pourtant, on sait que dans le cadre de la théorie des cordesthéorie des cordes, des objets aussi étranges que des espaces de Calabi-Yau, et surtout des orbifolds, sont plus ou moins des nécessités pour la cohérence de la théorie.

Vous avez attiré l'attention sur le fait que cela est un bon argument pour considérer que notre espace macroscopique puisse être topologiquement compliqué, car il ne serait qu'une partie, entrée en expansion, d'un espace à 10 ou 11 dimensions du type de ceux de la théorie des cordes. Cela fait-il de vous un partisan de la théorie des cordes ?

Jean-Pierre Luminet : C'est un peu plus compliqué que cela. À vrai dire, je n'ai pas d'opinion fixée sur la théorie des cordes et ce que j'en pense est encore en évolution. J'ai bien sûr trouvé la théorie des cordes très intéressante, mais, avec le temps et les difficultés qui s'accumulent, comme avec le problème du Landscape (véritable pied de neznez au critère de Popper), j'ai pris quelque distance avec elle et je m'interroge. Ceci dit, je ne serai pas aussi négatif à son sujet que des gens comme Lee Smolin ou Peter Woit.

Justement, le fait que l'espace macroscopique puisse avoir la topologie du modèle PDS ne pourrait-il pas servir de contrainte supplémentaire pour résoudre ce problème du Landscape et, si la théorie des cordes est la bonne, aboutir ainsi à des prédictions testables pour les massesmasses des particules par exemple ?

Jean-Pierre Luminet : On peut sans doute se poser la question et cela serait bien sûr formidable si cela arrivait, mais, dans l'état actuel de la théorie des cordes, il ne me semble pas évident du tout qu'on puisse y trouver la réponse, si toutefois elle y est contenue !

Revenons aux observations du rayonnement fossile. Au début de la courbe de puissance prédite par le modèle PDS, c'est-à-dire aux grandes longueurs d'onde, on voit que celle-ci oscille, contrairement à celle du modèle de concordance (voir la figure 3). Lorsque le satellite Plancksatellite Planck sera lancé, et qu'il aura mesuré plus finement cette courbe de puissance, le gain de résolution acquis permettra-t-il d'observer ces oscillations et donc de lever la dégénérescence entre PDS et de concordance les deux modèles, PDS et de concordance, autrement dit mieux les départager ? 

Figure 3. Cliquez pour agrandir. © OBSPM

Jean-Pierre Luminet : Malheureusement non. Planck va donner des informations aux courtes longueurs d'onde, à l'autre bout de la courbe. Le meilleur espoir que nous ayons, c'est d'arriver à extraire du signal que donnera Planck, les fameuses corrélations sous forme de cercles que Boudewijn Roukema et ses collègues semblent déjà voir avec les données de WMap.

Ce ne sera pas facile, il faudrait un rapport signal/bruit d'au moins 5 sigma pour que les corrélations observées soient vraiment vues comme une preuve du modèle PDS. Pour le moment, et même si c'est encourageant, ce rapport est de 2 sigma environ.

Une dernière question. Quid de l'inflation avec un modèle PDS ? Elle ne s'impose plus, et même, est-elle compatible avec ce genre de modèle de petit univers ?

Jean-Pierre Luminet : C'est une vaste question. Tout d'abord, il n'est pas vrai que le PDS permet de se passer de l'inflation pour expliquer l'homogénéité de l'Univers. Pour cela, il faudrait que celui-ci soit vraiment plus petit que ce que nous disent d'autres observations. Le point qui me semble le plus important, pour ce qui concerne la théorie de l'inflation, est qu'elle produise naturellement le bon spectre de fluctuations primordiales, et ce pour expliquer la formation des galaxies et leur rassemblement en amas pour donner les structures à grande échelle que nous observons. Toutefois, il ne faudrait pas croire que cela soit la seule possibilité. Il existe des alternatives à l'inflation qui produisent, elles aussi, un bon spectre de fluctuations.

Si l'inflation a bien eu lieu, elle ne peut pas avoir été trop importante dans le cadre d'un modèle PDS plus petit que l'horizon. En termes techniques, l'e-folding, la puissance de l'exponentielle donnant la valeur de l'étirement de l'espace lors de la phase inflationnaire, devrait être de l'ordre de 60 environ. Ce résultat est en fait assez général pour des Univers clos.

Il se trouve qu'Andrei Linde a étudié des modèles clos et à topologie multiplement connexe. Il a montré que moyennant quelques ajustements fins, ceux-ci étaient parfaitement compatibles avec l'inflation. Il a étudié en particulier des modèles clos dont la courbure est nulle, voire négative, mais avec une topologie non triviale. Sa conclusion est que ce genre de modèle pourrait être la règle plutôt que l'exception dans le cadre de la cosmologie quantique. La théorie de l'inflation est extraordinairement flexible, peut-être trop d'ailleurs...