Les sursauts gamma se répartissent pour la plupart en deux grandes classes, les uns causés par des hypernovae, les autres par des collisions d'étoiles à neutrons. Selon des simulations numériques de Matthieu Brassart et Jean-Pierre Luminet, de l'Observatoire de Paris-Meudon, certains sursauts s’expliqueraient par l’effet des forces de marée des trous noirs galactiques lorsqu’une étoile passant près de leur horizon est  aplatie deux fois avant d'être déchiquetée par une explosion thermonucléaire.

au sommaire

    Une vue d'artiste montrant la dislocation d'une étoile passée trop près d'un trou noir. Elle est d'abord aplatie comme une crêpe par les forces de marée avant d'exploser en libérant du gaz avalé par le trou noir. Crédit : Nasa-CXCM, Weiss

    Une vue d'artiste montrant la dislocation d'une étoile passée trop près d'un trou noir. Elle est d'abord aplatie comme une crêpe par les forces de marée avant d'exploser en libérant du gaz avalé par le trou noir. Crédit : Nasa-CXCM, Weiss

    C'est une année qui commence en fanfare pour Jean-Pierre Luminet, l'astrophysicienastrophysicien et cosmologiste bien connu des lecteurs de Futura-Sciences. Après avoir publié sa dernière biographie romancée des fondateurs de l'astronomie moderne, La perruque de Newton, dans laquelle il montre que le symbole de la science positiviste, Isaac NewtonIsaac Newton, était aussi « le dernier des magiciens », selon les mots de l'économiste britannique John Keynes , il  propose aujourd'hui, avec son collègue Matthieu Brassart, une nouvelle explication pour rendre compte des sursauts gamma.

    Pour la comprendre il faut remonter aux travaux d'Edouard Roche, le mathématicienmathématicien et astronomeastronome français à l'origine de la fameuse limite de Roche. Elle exprime le fait qu'il existe une distance limite d'approche d'un petit corps céleste au voisinage d'un corps plus grand.

    Edouard Roche. Crédit : Université Montpellier 2

    Edouard Roche. Crédit : Université Montpellier 2

    En deçà, les forces de marée du corps principal sont si importantes qu'elles disloquent le petit corps, incapable de maintenir sa cohésion sous sa propre gravité. Originellement limitée aux planètes, la notion de limite de Roche a été étendue à la stabilité des amas globulaires et des petites galaxies approchant des grandes et on parle alors de rayon de marée. Cette même notion de rayon de marée est utilisée aussi lorsqu'une étoile approche d'un trou noirtrou noir.

    En mars 1982, Jean-Pierre LuminetJean-Pierre Luminet et Brandon Carter avec déjà publié dans le journal Nature un article dans lequel ils avaient montré qu'une étoile pénétrant dans la zone définie par le rayon de marée d'un trou noir galactique devait d'abord être aplatie comme une crêpe par les forces de marée. Dans un second temps, expliquaient-ils, des réactions thermonucléaires doivent se produire au sein de l'étoile, conduisant à des détonations capables de la disloquer.

    Cliquer pour agrandir. L'écrasement d'une étoile par les forces de marée d'un trou noir. Le dessin illustre la déformation progressive d'une étoile plongeant profondément dans le rayon de marée d'un trou noir géant (la taille de l'étoile est considérablement agrandie pour la clarté du dessin). La figure du haut représente la déformation de l'étoile dans son plan orbital (vue de dessus), celle du milieu montre la déformation dans la direction perpendiculaire (vue par la tranche), et le diagramme du bas indique l'aplatissement relatif. De (a) en (d), les forces de marée sont faibles et l'étoile reste pratiquement sphérique. En (e), l'étoile pénètre dans le rayon de marée et est dès lors condamnée. Sa configuration se rapproche d'abord de celle d'un cigare, puis de (e) à (g), l'effet de laminoir des forces de marée écrase l'étoile dans son plan orbital, en une configuration de « crêpe ». Puis l'étoile rebondit et se dilate en ressortant du rayon de marée en (h). Plus loin sur son orbite, l'étoile finit par se dissocier en fragments gazeux. Les simulations hydrodynamiques détaillées, prenant en compte les ondes de choc, ont été effectuées durant la phase d'écrasement (e) à (g). Crédit : Jean-Pierre Luminet, Matthieu Brassart

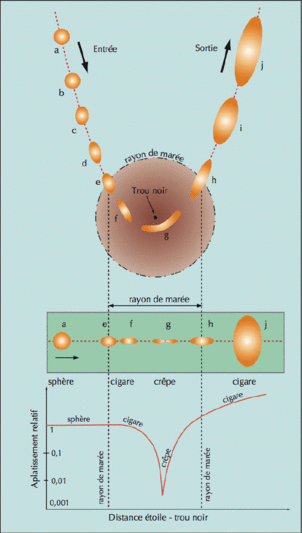
    Cliquer pour agrandir. L'écrasement d'une étoile par les forces de marée d'un trou noir. Le dessin illustre la déformation progressive d'une étoile plongeant profondément dans le rayon de marée d'un trou noir géant (la taille de l'étoile est considérablement agrandie pour la clarté du dessin). La figure du haut représente la déformation de l'étoile dans son plan orbital (vue de dessus), celle du milieu montre la déformation dans la direction perpendiculaire (vue par la tranche), et le diagramme du bas indique l'aplatissement relatif. De (a) en (d), les forces de marée sont faibles et l'étoile reste pratiquement sphérique. En (e), l'étoile pénètre dans le rayon de marée et est dès lors condamnée. Sa configuration se rapproche d'abord de celle d'un cigare, puis de (e) à (g), l'effet de laminoir des forces de marée écrase l'étoile dans son plan orbital, en une configuration de « crêpe ». Puis l'étoile rebondit et se dilate en ressortant du rayon de marée en (h). Plus loin sur son orbite, l'étoile finit par se dissocier en fragments gazeux. Les simulations hydrodynamiques détaillées, prenant en compte les ondes de choc, ont été effectuées durant la phase d'écrasement (e) à (g). Crédit : Jean-Pierre Luminet, Matthieu Brassart

    Ce travail a depuis été repris une première fois par Jean-Pierre Luminet pour faire l'objet de simulations numériquessimulations numériques en collaboration avec son collègue Matthieu Brassart.

    Il vient maintenant d'être étendu au cas où l'étoile passe si près de l'horizon d'un trou noir galactique qu'elle se retrouve sur une trajectoire parabolique la conduisant à subir deux compressions successives lors de son périple autour du trou noir.

    Cliquer pour agrandir. A gauche : orbite parabolique d'une étoile plongeant profondément dans le rayon de marée d'un trou noir de 1 million de masses solaires. Le petit cercle en trait plein représente le rayon gravitationnel du trou noir et le grand cercle en pointillés le rayon de marée. Le facteur de pénétration, c'est-à-dire le rapport entre le rayon de marée et la distance au périastre, est de 9. Comme l'orbite stellaire s'entrecoupe à l'intérieur du rayon de marée, le champ gravitationnel du trou noir induit deux compressions successives, qui se produisent aux points de l'orbite marqués en noir.<br />A droite : évolution temporelle de la pression centrale (en unités de sa valeur initiale). Celle-ci contrecarre deux fois l'effondrement en chute libre de la matière stellaire, une fois avant le passage au périastre (à t=0), puis une centaine de secondes plus tard. Crédit : Jean-Pierre Luminet, Matthieu Brassart

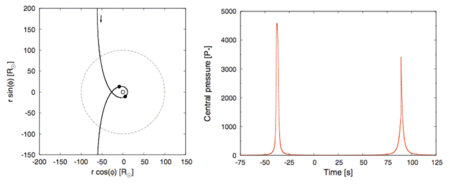
    Cliquer pour agrandir. A gauche : orbite parabolique d'une étoile plongeant profondément dans le rayon de marée d'un trou noir de 1 million de masses solaires. Le petit cercle en trait plein représente le rayon gravitationnel du trou noir et le grand cercle en pointillés le rayon de marée. Le facteur de pénétration, c'est-à-dire le rapport entre le rayon de marée et la distance au périastre, est de 9. Comme l'orbite stellaire s'entrecoupe à l'intérieur du rayon de marée, le champ gravitationnel du trou noir induit deux compressions successives, qui se produisent aux points de l'orbite marqués en noir.
    A droite : évolution temporelle de la pression centrale (en unités de sa valeur initiale). Celle-ci contrecarre deux fois l'effondrement en chute libre de la matière stellaire, une fois avant le passage au périastre (à t=0), puis une centaine de secondes plus tard. Crédit : Jean-Pierre Luminet, Matthieu Brassart

    Les calculs d'hydrodynamique de l'intérieur de l'étoile en régime relativiste montrent que des ondes de chocs se produisent et chauffent la surface à trois reprises avant l'explosion thermonucléaire de l'astreastre. La surface de l'astre atteint alors des températures de l'ordre du milliard de degrés, ce qui doit générer d'importantes émissionsémissions dans le domaine des rayons gammarayons gamma.

    Evolution temporelle de la température (l'étoile passe au périastre à t=0). La courbe en traits pleins retrace la température au centre de l'étoile. La compression induit un premier maximum à environ 2.10<sup>8</sup> K durant environ 4 secondes, et environ 115 secondes plus tard, une seconde compression de même amplitude durant environ 6 secondes.<br />La courbe en pointillés donne la température transportée par les ondes de choc. Les trois maxima sont atteints à la surface stellaire. Celle-ci est d'abord portée à environ 4.10<sup>9</sup> K durant environ 0,03 s, puis à environ un milliard de kelvins durant environ 1,5 seconde, ensuite à environ 10<sup>9</sup> K durant environ 3 secondes. Crédit : Jean-Pierre Luminet, Matthieu Brassart

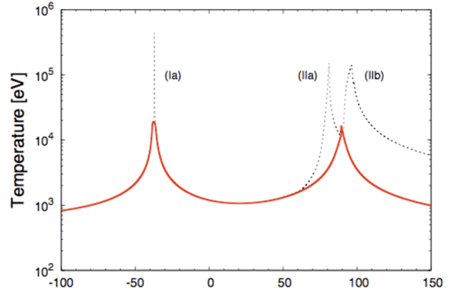
    Evolution temporelle de la température (l'étoile passe au périastre à t=0). La courbe en traits pleins retrace la température au centre de l'étoile. La compression induit un premier maximum à environ 2.108 K durant environ 4 secondes, et environ 115 secondes plus tard, une seconde compression de même amplitude durant environ 6 secondes.
    La courbe en pointillés donne la température transportée par les ondes de choc. Les trois maxima sont atteints à la surface stellaire. Celle-ci est d'abord portée à environ 4.109 K durant environ 0,03 s, puis à environ un milliard de kelvins durant environ 1,5 seconde, ensuite à environ 109 K durant environ 3 secondes. Crédit : Jean-Pierre Luminet, Matthieu Brassart

    Remarquablement, on connaît quelques courbes de lumièrelumière associées à des sursautssursauts gamma qui présentent justement des pics de luminositéluminosité successifs que l'on expliquait mal jusqu'ici. Si l'on se fie à la densité d'étoiles au voisinage des trous noirs galactiques, comme celui occupant le centre de notre Voie lactée, on peut s'attendre à des sursauts gamma de ce type tous les mille à cent mille ans.