Histoire des mesures géodésiques

Les grands initiateurs de travaux géodésiques furent les Alexandrins, plus particulièrement ÉratosthèneÉratosthène de Cyrène. Puis, le renouveau de la géodésie moderne du XVI^e siècle apporta de réels progrès. Enfin, à partir de 1960, grâce à l'avènement des techniques spatiales, le champ de pesanteur put être alors mesuré et cartographié avec une précision inespérée.

Quelle est l'histoire des mesures géodésiques ? © Merkushev Vasiliy, Shutterstock

Grand savant grec à la fois astronomeastronome, mathématicienmathématicien, géographe, géomètregéomètre, philosophe, grammairien et poète, Ératosthène de Cyrène est né en 276 av. J.-C. à Cyrène, une ville d'Afrique septentrionale. Il fut nommé grand directeur de la bibliothèque d'Alexandrie en 240 av. J.-C. à la demande de PtoléméePtolémée III, pharaon d'Égypte, et connut ArchimèdeArchimède. En astronomie, il calcula l'obliquité de l'écliptiqueécliptique avec une erreur négligeable. Il décida aussi de rassembler toutes les mesures connues à son époque pour rénoverrénover la cartographie.

Portrait d'Ératosthène. © DP

Mesurer la circonférence de la Terre

Ératosthène envisagea sérieusement, tout comme Pythagore avant lui, que la Terre était une sphère, et mit au point une méthode géométrique permettant de calculer la circonférence de notre planète. Il est important de présenter ici ces mesures car les résultats seront la base d'autres mesures géodésiques et feront l'objet de multiples controverses.

Pythagore peint par Raphaël. © DP

La ville de Syène (Assouan de nos jours) se situe à peu près sur le tropiquetropique du cancercancer. Ératosthène considéra que Syène et Alexandrie étaient sur le même méridien ou bien parvint, grâce aux cartes dont on sait qu'il disposait, à estimer la différence de latitudelatitude entre les deux villes. Le jour du solstice d'été, en 205 av. J.-C., à Alexandrie, il constata que les rayons du soleil formaient avec l'extrémité d'un obélisque (ou un bâtiment) un angle de 7°12', alors qu'à Syène, au même moment, les rayons tombaient à la verticale en éclairant le fond d'un puits.

L'hypothèse étant que les rayons arrivant à Syène et à Alexandrie étaient parallèles, il en déduisit que la distance entre ces deux villes (arpentée à pied par les hommes pour des échanges commerciaux), soit 5.000 stades, équivalait à l'angle produit par les rayons solaires sur l'obélisque, soit 7°12', c'est-à-dire à peu près un cinquantième de la circonférence (360°), donc estimée à 250.000 stades.

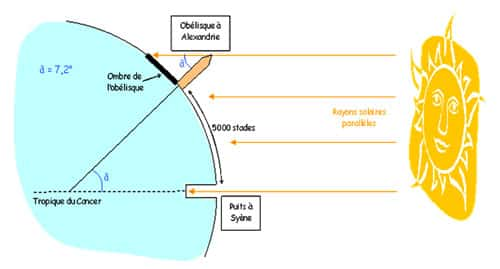
L'hypothèse étant que les rayons arrivant à Syène et à Alexandrie étaient parallèles, Ératosthène en déduisit que la distance entre ces deux villes (arpentée à pied par les hommes pour des échanges commerciaux), soit 5.000 stades, équivalait à l'angle produit par les rayons solaires sur l'obélisque, soit 7°12', c'est-à-dire à peu près un cinquantième de la circonférence (360°), donc estimée à 250.000 stades. © DR

Quelques érudits pensent aujourd'hui qu'il pourrait y avoir des erreurs quant à l'étalonnage de l'unité du « stade ». En effet, sa valeur était variable selon les contrées (selon les historienshistoriens, un stade équivaudrait à environ 160 m) ; Ératoshène aurait donc calculé une circonférence oscillant entre 39.700 et 46.600 km, ce qui est extraordinairement précis pour l'époque. Il est donc important d'utiliser ces mesures avec prudence. Un autre astronome, Posidonius, né à Apamée, sur l'Oronte (Syrie actuelle), en 135 av. J.-C., redonna une autre approximation, mais sans plus.

La géodésie à la Renaissance

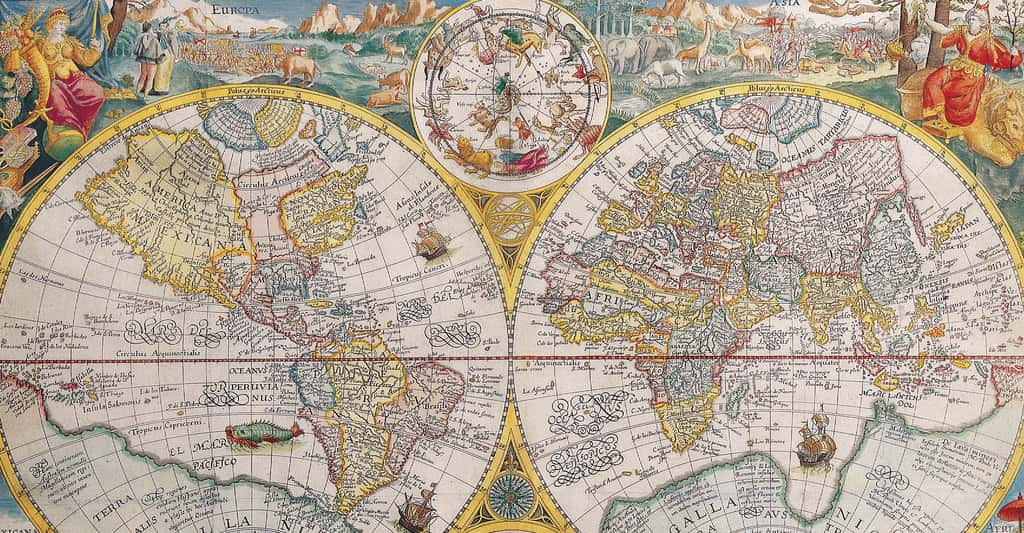
Le renouveau de la géodésie moderne du XVI^e siècle apporta de réels progrès. Gérard Mercator, qui amena une avancée décisive pour la suite des mesures terrestres, est un des plus connus. Né à Rupelmonde en 1512, ce géographe publia un nouveau type de projection plane cartographique en 1569, particulièrement utile et efficace pour les navigateursnavigateurs dans un premier temps, la « projection cylindrique de Mercator » dans le système UTM (Universal Transverse Mercator). Le principe est de projeter les points 3D du globe sur une surface cylindrique que l'on déploie.

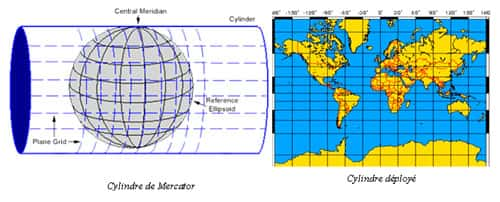
Gérard Mercator publia un nouveau type de projection plane cartographique en 1569, la « projection cylindrique de Mercator » dans le système UTM (Universal Transverse Mercator). © DR

On vit à ce moment-là surgir les premiers arpenteursarpenteurs effectuant surtout des travaux pour le cadastrecadastre, bien que le métier soit déjà attesté depuis le XIII^e siècle. Les courants de pensée du XVI^e siècle changèrent, suscitèrent de nouvelles approches et de nouvelles techniques. On envisagea alors les mesures à grande échelle, et donc d'arpenter la Terre entière. Les savants qui se lanceront dans l'aventure un siècle plus tard s'approprieront légitimement le titre d'arpenteur.

En fait, le personnage clé de cette époque est incontestablement Gemma Frisius. Né à Dokkum, au nord de la Hollande, en 1508, il fut médecin, astronome et mathématicien. En 1530, il proposa une méthode pour déterminer la longitudelongitude d'un lieu à partir de la différence des heures données à un moment « m » par des horloges réglées sur les astresastres. Il établit un traité en 1533, à Anvers, le Libellus De Locorum Describendorum Ratione, qui fonde en 16 pages les bases de la géodésie moderne. Il s'agit du plus ancien exposé des principes de triangulationprincipes de triangulation géodésique. Il y explique comment des réseaux de triangles permettent d'arpenter des espaces aussi vastes qu'on le désire.

En 1537, il n'en resta pas là et décrivit alors la constructionconstruction de l'instrument dérivé de l'astrolabe, destiné à ces mesures de terrain : le « goniomètregoniomètre » (en y ajoutant une boussole, Gualterus Arsenius, son neveu, perfectionna l'instrument). Ses œuvres successives en firent le chef de l'école de géographie néerlandaise, dont son élève Gérard Mercator fut le plus brillant représentant.

C'est Jacob van Deventer qui mit en pratique les méthodes de triangulation de Gemma Frisius. Il les utilisa pour réaliser la carte des Pays-Bas la plus précise jusqu'alors.

Quelques instruments de mesure et d'observation inventés par Tycho Brahe. © DR

D'autres arpenteurs suivirent et l'on vit apparaître les premières cartes complètes en Angleterre, en Allemagne et en France. Ces nouvelles méthodes furent appliquées par Kepler lui-même. Ces nouvelles approches bénéficièrent aussi des progrès continus en matièrematière d'instruments de mesures géodésiques.

Ce fut au tour de Jesse Ramsden de s'illustrer en inventant, en Angleterre, le théodolite, qui est un instrument de mesure des angles horizontaux. Ce personnage était le plus réputé des fabricants d'instruments scientifiques. En réalité, le mathématicien Leonard Digges décrivit le premier un instrument de mesure angulaire en 1571 dans son livre Pantometria. Jesse Ramsden le construisit seulement en 1782.

Portrait de Tycho Brahe. © DP

Tycho Brahe (1546 à 1601), né en Scanie, une province soumise à cette époque au royaume du Danemark et qui se trouve actuellement en Suède, est un physicienphysicien et observateur émérite. Il observe dès ses 17 ans une conjonctionconjonction entre JupiterJupiter et SaturneSaturne et décèle des erreurs dans les tables astronomiques existantes. Il établira de nouvelles tables à partir de ses propres observations. Il fonda plus tard après ses études un observatoire à Uraniborg, sur l'île de Hven, entre le Danemark et la Suède, afin de mesurer avec précision sa position en utilisant les ascensions droitesascensions droites et déclinaisonsdéclinaisons de 777 étoilesétoiles, connues grâce à plusieurs années d'observation, et qui servirent par la suite à Kepler, son disciple, pour découvrir les lois régissant le mouvement des planètes. Son premier ouvrage fut dédié à la découverte d'une supernovasupernova dans la constellationconstellation de Cassiopée.

Développement de la géodésie

Au XVII^e siècle, l'abbé Jean Picard (1620-1682), astronome français, mit au point des appareils optiques de mesure d'angle, et se rendit à Uraniborg pour en déterminer ses coordonnées par des visées astronomiques. Ce spécialiste de la géodésie rédigea deux importants traités qui parurent en ouvrages posthumes en 1684 : La mesure de la Terre et Traité du nivellement.

Gaspard Monge. © DP

Un grand et brillant géomètre du XVIII^e siècle fit beaucoup pour améliorer toujours plus les techniques de mesures géodésiques, Gaspard Monge (1746-1818), né à Beaune. Ses talents de géomètre et de mathématicien ne tardèrent pas à se dévoiler. Il présenta plusieurs mémoires à l'Académie des sciences sur les thèmes de la géométrie différentielle, de la géométrie descriptive, du calcul des variationscalcul des variations... Il fut alors élu associé géomètre de l'Académie des sciences. La révolution bouleversa sa vie. Il soutint ardemment les évènements révolutionnaires. Après cette période, il s'intéressa à l'armement. Il enseigna de nouvelles solutions de fabrication de poudre à canon. Il créa en 1794 l'ECTP (École centrale des travaux publics), qui deviendra un an plus tard l'École polytechnique, où les savants les plus prestigieux, comme Arago, PoissonPoisson, Fresnel, y firent leurs études et y enseignèrent, pour certains, les matières actuelles. Mais ces élèves studieux se montraient très indisciplinés à l'extérieur de l'école, lors de missions scientifiques et c'est Napoléon, en 1804, qui décida de donner à celle-ci un régime militaire et de caserner les élèves, avec pour devise « Pour la patrie, les sciences et la gloire ».

De nouveaux progrès apparurent dans la détermination des formes de la Terre. John Fillmore Hayford (1868-1925), un ingénieur en géodésie aux États-Unis mit au point une méthode qui ne reposait plus sur les mesures d'arcs, mais d'aires, et qui permit d'obtenir de bien meilleurs résultats. Pour améliorer encore les mesures géodésiques, il proposa en 1899 une formulation du principe d'isostasieisostasie (qui concerne l'équilibre des massesmasses des continents et celle de l'écorce océanique) seulement à titre d'hypothèse, mais qui devint alors un des fondements de la géophysique.

Au XIX^e siècle, les jonctions géodésiques entre les principaux réseaux de triangulation existant alors devinrent une occupation importante. Mais, dès les premières décennies du XX^e siècle, le problème devint l'unification globale des modes de représentations géodésiques. Le Canada et le Mexique adoptèrent en 1913 le système de référence des États-Unis, qui devint en 1927 le système « nord-américain ». Le gros du travail de réunification des systèmes fut tenté au lendemain de la seconde guerre mondiale, mais celle-ci ne fut jamais obtenue. Aujourd'hui, cohabitent ainsi plusieurs systèmes géodésiques mondiaux, chacun ayant des propriétés et paramètres bien particuliers ; ils sont donc utilisés en fonction soit des habitudes, soit des critères techniques définis par la tâche qui les requiert.

À l'opposé des systèmes géodésiques qui, pour l'essentiel, s'achèvent au cours du XX^e siècle, la gravimétriegravimétrie, à peine à l'ébauche au siècle précédent, prend désormais un essor extraordinaire. Dans un premier temps, c'est grâce au perfectionnement des techniques classiques (le pendule de Vening Meinesz, le gravimètre d'interpolation...). Ensuite, à partir de 1960, c'est grâce à l'avènement des techniques spatiales. Le champ de pesanteur peut être alors mesuré et cartographié avec une précision inespérée. On peut ainsi en étudier son évolution au fil du temps, ou connaître la topographie du fond des océans. La géodésie spatiale (GPSGPS, télémètres laserlaser, doppler, radar...) peut également mettre en évidence les mouvementsmouvements verticaux de l'écorce terrestre aussi bien que les déplacements horizontaux des plaques tectoniquesplaques tectoniques. Les irrégularités de la forme de la Terre offrent une vision nouvelle de notre belle planète.