au sommaire
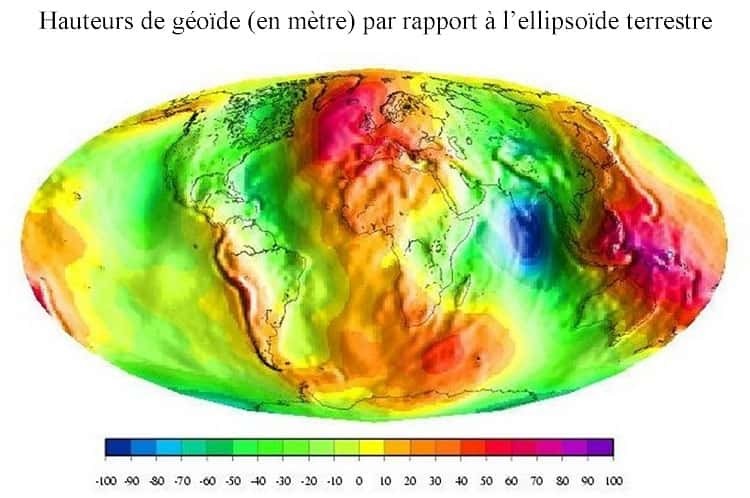
Pour parler du niveau de la mer et de ses variations il faut une référence géométrique fixe : c'est l'ellipsoïde de référence qui est au plus prés de la forme de la Terre.
Par rapport à cette référence absolue le niveau des océans est la somme de deux composantes.
La surface des eaux tranquilles
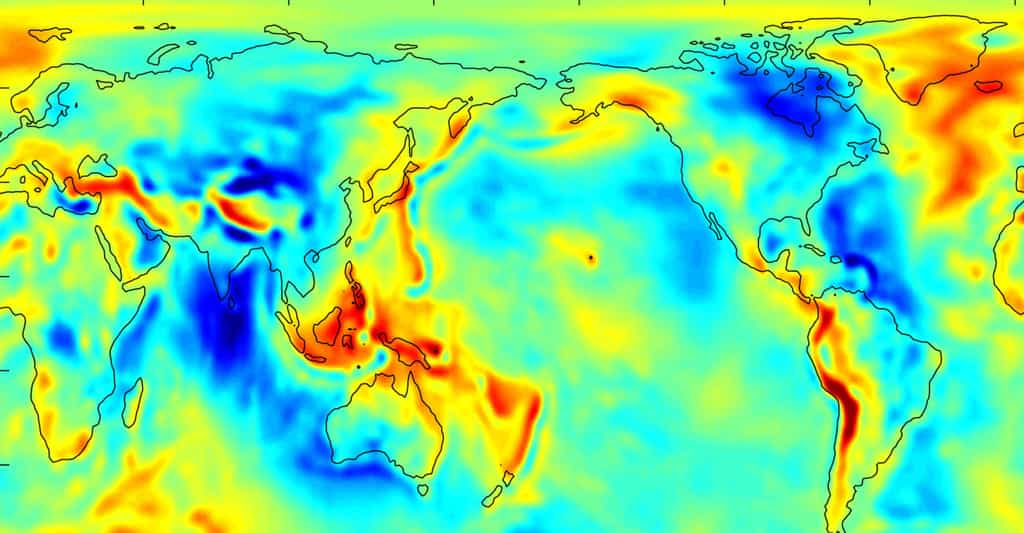
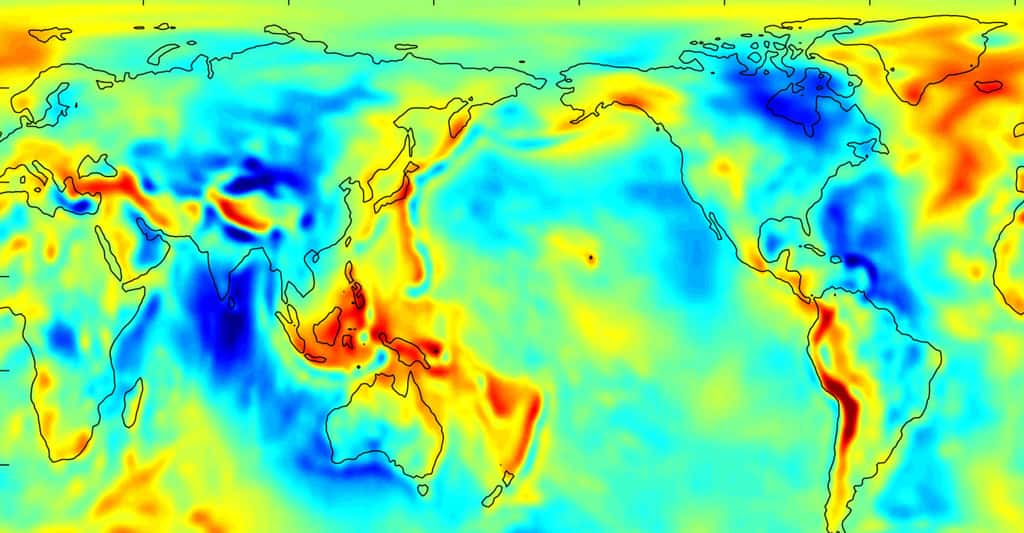
La première représente la surface qui serait celle des océans en l'absence de tout mouvement, ce que naguère on appelait la « surface des eaux tranquilles » pour illustrer l'horizontale. C'est une surface équipotentielle du champ de pesanteur ou géoïdegéoïde ; c'est-à-dire qu'en en tout point la force de pesanteur lui est perpendiculaire. Comme la Terre n'est pas homogène, la pesanteur à sa surface varie et la surface de l'océan, géoïde, épouse les variations spatiales du champ de pesanteur qui font du « géoïde » une sorte de patatoïde fait de creux et de bosses.
Ainsi par exemple entre l'océan Indien au sud de l'Inde et le Pacifique ouest du côté de l'Indonésie observe-t-on, par rapport à l'ellipsoïde de référence, une différence de niveau de la surface de l'océan-géoïde proche de 150 mètres.
La topographie dynamique de la surface de l’océan
La deuxième composante est due aux mouvements de l'océan et aux courants qui induisent par rapport à ce géoïde des variations du niveau de la mer : c'est ce que l'on appelle la topographie dynamique de la surface de l'océan dont, on déduit les courants marins.
Si l'on s'intéresse aux variations du niveau moyen des océans c'est l'ellipsoïde géométrique qu'il faut prendre comme référence ; si ce sont les courants et leurs variations (la dynamique) qui nous préoccupent c'est le géoïde la bonne référence.