au sommaire

Forçage naturel : forçage solaire et mesures de l’irradiance solaire
Le rayonnement solairerayonnement solaire est peu différent de celui d'un corps noir à 5.800 kelvins. Il est issu de la photosphère du Soleil qui correspond donc à la zone visible. L'irradiance solaire totaleirradiance solaire totale (ou TSI) est l'intensité totale du rayonnement solaire reçu par une surface de 1 m2, perpendiculaire à la direction du Soleil, au sommet de l'atmosphèreatmosphère. Elle dépend de la température moyenne de la photosphère solaire, du rayon du Soleil et de la distance Terre-Soleil [1].

Figure 6. Taches solaires. © Nasa
Mesures de l’irradiance solaire
Les premières tentatives de mesure de la TSI ont commencé dans les années 1830, avec des mesures indépendantes par Claude Pouillet et John Herschel, mais elles étaient près d'un facteur deux trop faibles en raison de l'absorptionabsorption atmosphérique. Même les mesures depuis des ballons dans les années 1900 manquaient de la précision instrumentale nécessaire pour détecter des changements de l'ordre de 0,1 %. Ce ne fut que lorsque les mesures spatiales ont été disponibles que les changements de TSI ont pu être mesurés et l'idée fausse d'une « constante solaireconstante solaire » a changé. Ces mesures ont démarré avec le lancement du satellite Nimbus 7 en Novembre 1978, bientôt suivi par un radiomètreradiomètre à cavité (Active Cavity Radiometer Irradiance Monitor : Acrim) sur la mission Solar Maximum et par l'expérience Earth Radiation Budget Experiment (Erbe). Puis, les deuxième et troisième instruments Acrim ont été lancés, de même que deux instruments sur la NasaNasa/Esa Solar and Heliosphère Observatory (Soho).
Les divers ensembles de données sont globalement en accord et démontrent de manière concluante que les variations de la TSI suivent le passage des taches sur le disque solaire avec une amplitude d'environ 0,2 %, et que, à long terme, les variations du cycle solaire ne sont que de l'ordre de 0,1 %.
Depuis 2003, l'expérience Sorce (Solar Radiation and Climate Experiment) poursuit ces observations avec une meilleure précision, de l'ordre de ± 0,01%.
Ces différents instruments n'ont pas fonctionné tous en même temps et il existe un désaccord significatif entre eux. Pour mesurer l'irradiance solaire, on utilise des radiomètres à cavité (ou encore dits absolus).
Principes et difficultés des mesures par radiomètres à cavité
Le principe est simple : il s'agit de piéger le rayonnement au sein d'une cavité et de l'absorber, le rayonnement est alors transformé en chaleurchaleur et on détermine la puissance électrique nécessaire pour le maintenir à température constante. C'est simple à dire mais quand on cherche une précision de l'ordre de 0,01 %, il faut que, au minimum, 99,99 % du rayonnement soit absorbé dans la cavité. Puisque le rayonnement non observé est réfléchi, il faut que la réflectance de la cavité à toutes les longueurs d'ondelongueurs d'onde du spectrespectre soit inférieure à 0,0001.
Pour obtenir ce résultat, on dessine la cavité de façon à ce que le rayonnement non absorbé soit réfléchi sur les parois de nombreuses fois avant d'éventuellement sortir. Il n'empêche que la réflectance n'est pas parfaitement nulle. Cela a des conséquences non seulement sur la calibration absolue de l'appareil mais aussi sur l'évolution de celle-ci : il y a dégradation dans le temps car les parois, surtout les plus proches de l'ouverture, sont exposées au rayonnement solaire, y compris à la partie la plus énergétique, au vent solairevent solaire et même au rayonnement cosmique.
Dans un premier temps, immédiatement après le lancement, les parois proches de l'ouverture de la cavité sont rapidement attaquées, leurs propriétés d'absorption changent, cela se traduit par une augmentation temporaire de la sensibilité, par la suite, la dégradation entraîne une baisse de la sensibilité dans le temps ce qui se traduit par une apparente diminution de la TSI. Pour y remédier, on a maintenant recours à un second radiomètre qui n'est utilisé que ponctuellement en tant que référence. Il y a donc des corrections à apporter aux mesures. Comme les périodes de fonctionnement des différents instruments ne se recouvrent que partiellement, il faut composer les mesures des différents instruments après leur avoir fait subir ces corrections.
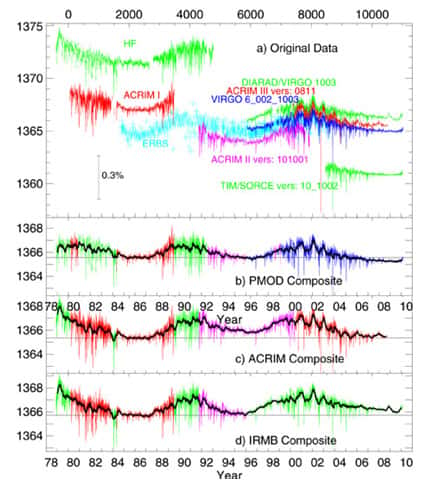
Figure 7. Valeurs moyennes journalières de l’irradiance solaire totale (TSI) mesurée par différents radiomètres et reconstructions composites selon trois sources différentes (voir texte). © pmodwrc.ch
La figure 7 présente les mesures brutes des différents instruments disponibles ainsi que les trois reconstructions qui en ont été dérivées. La différence essentielle réside dans la façon dont on fait la liaison entre les données de Acrim I et Acrim II. Les trois reconstructions utilisent les observations des instruments qui étaient en fonctionnement pendant cette période, c'est-à-dire celles de l'instrument HF (expérience ERB à bord du satellite Nimbus7) et celles de l'expérience Erbe à bord du premier satellite dédié à la mesure du bilan radiatif ERBS. La reconstruction PMOD corrige un problème de pointage connu de l'instrument HF, tandis que celle nommée Acrim n'en tient pas compte.
Cette différence se traduit dans les variations de la TSI entre les deux précédents minimum (86 et 96) : pour Acrim, la TSI augmente de 0,6 W/m2 alors que pour PMOD, la variation est négligeable. [2]
L'approche de PMOD a été validée par des expériences de vieillissement en synchrotron, elle est aussi la seule qui s'accorde avec les mesures du champ magnétiquechamp magnétique solaire. Le débat n'est pas clos mais PMOD est aussi la seule reconstitution qui montre une variation similaire à celle du nombre de taches solairestaches solaires (la TSI croît avec le nombre de taches), on peut donc extrapoler.
[1] Notez que, entre la périhéliepérihélie qui a lieu le 4 janvier et l'aphélieaphélie du 4 juillet, la distance au Soleil varie de 3,3 %, ce qui donne une variation de la « constante solaire » de près de 85 W/m2, équivalente à un forçage périodique de 15 W/.m2
[2] Cette variation éventuelle est celle de la TSI, pour en déduire le forçage, il faut la multiplier par un facteur (1-A)/4 où A = 0,3 est l'albédoalbédo et le facteur ¼ traduit la sphéricité de la Terre. Le forçage serait donc de 0,1 W/m2.