au sommaire
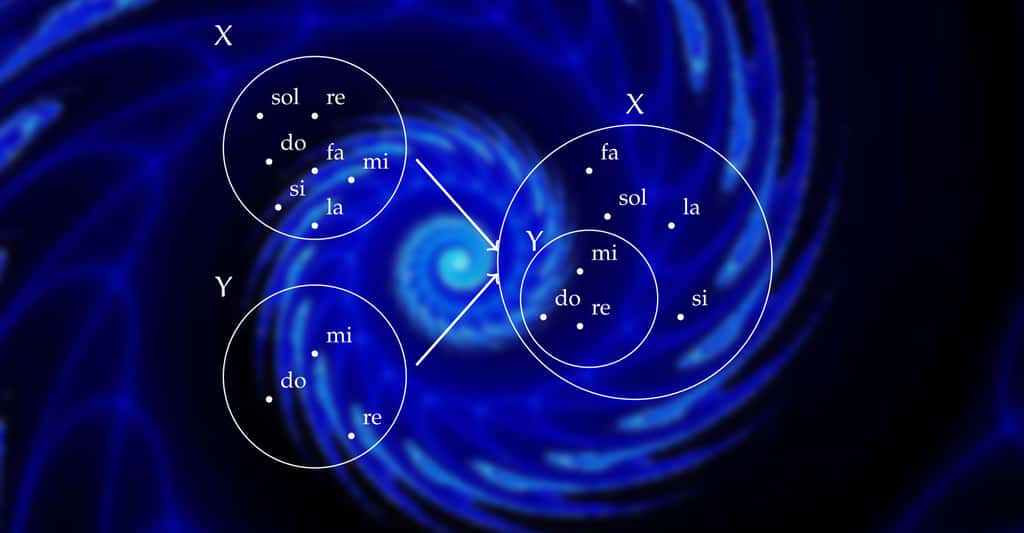
Pour résoudre le paradoxe du tout et des parties et affronter l'hypothèse du continu, notre idée de l'infini actuel doit évoluer ; aujourd'hui encore, nous découvrons de nouveaux infinis.

L'infini est-il paradoxal en mathématiques ? © Agsandrew, Fotolia
L'infini mathématique peut-il être maîtrisé ? Autrement dit, peut-on faire une théorie de l'infini qui évite tout paradoxe et toute incohérence ? Pour répondre à ces questions, nous distinguerons paradoxes et situations logiquement peu satisfaisantes.
Un paradoxe au sein d'une théorie est la possibilité de démontrer une chose et son contraire. Dans cette situation, tout en n'utilisant que des raisonnements fondés sur les axiomes de la théorie, nous pouvons en tirer une affirmation A et l'affirmation contraire Non A. En mathématiques, les paradoxes (on les dénomme aussi contradictions, inconsistances, antinomies) sont inacceptables, et les logiciens font tout pour les éviter.

Le paradoxe de l’hôtel de Hilbert (à découvrir à la page suivante) montre pourquoi des ensembles infinis ont longtemps paru absurdes. © Belin
Aujourd'hui, les mathématiciens connaissent toutes sortes de moyens pour contourner les paradoxes au sein des théories mathématiques de l'infini. La question subsiste : ces moyens atteignent-ils leurs fins ?
Une situation logiquement insatisfaisante apparaît lorsqu'une théorie nous permet d'énoncer des propriétés étonnantes, parfois opposées à notre attente, sans toutefois qu'une véritable contradiction apparaisse. Nous pouvons alors continuer à développer la théorie en espérant que la difficulté sera résolue plus tard. Parfois, nous finissons par accepter la situation jugée gênante, et ce qui était perçu comme douteux devient alors banal, comme si une métamorphosemétamorphose de nos conceptions profondes s'était produite.
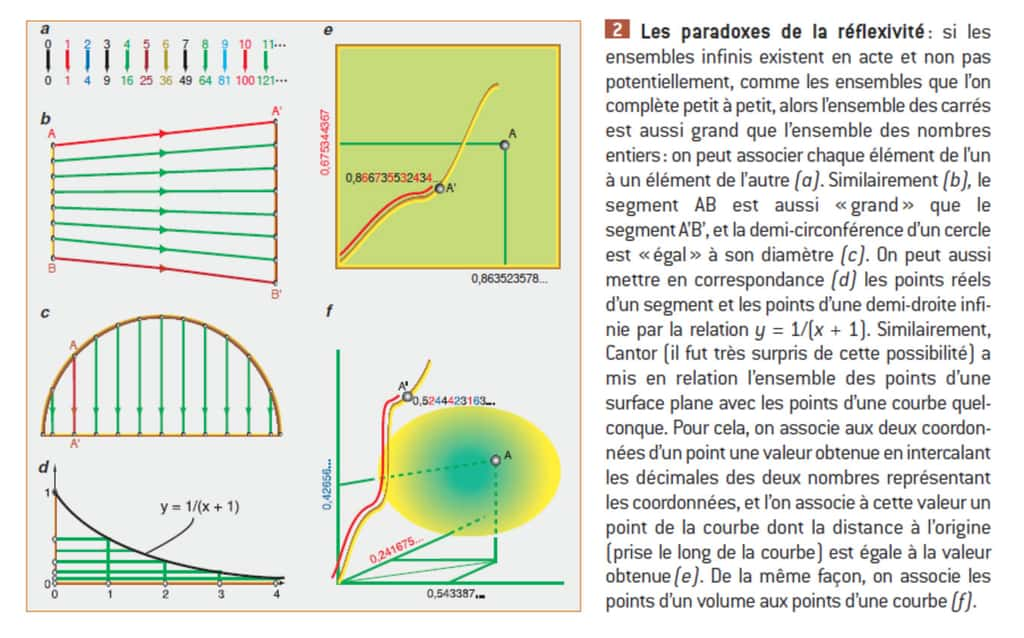
Quelques exemples pour illustrer la réflexivité, sur laquelle Cantor a notamment travaillé. © Belin
Quelle est aujourd'hui la situation entre paradoxes infinis, situations insatisfaisantes tolérées et digérées ? Pour le savoir, nous allons passer en revue quelques paradoxes de l'infini mathématique, paradoxes qui décidèrent de son histoire. À chaque fois, nous évoquerons les solutions mathématiques avancées et nous nous interrogerons pour savoir si ces solutions sont satisfaisantes en tout point ou si, au contraire, elles laissent des zones d'ombre qui marquent la limite de cette prétendue maîtrise de l'infini par le formalisme des mathématiques modernes.