Principe de calcul de coordonnées

La position de points disposés à la surface terrestre et qui sont connues en coordonnées cartésiennes tridimensionnelles géocentriquesgéocentriques ou géographiques, ne peut être représenté que sur un globe, ce qui est très encombrant et peu maniable sur le terrain. Aussi pour beaucoup d'opérations, il faut arriver à une représentation cartographique plane, permettant de travailler sur papier que l'on appelle projection plane.

Le passage de ces coordonnées fastidieuses à des coordonnées rectangulaires planes en 2 dimensions, suppose de ramener tout d'abord tous les points de la surface réelle terrestre sur un ellipsoïde de référence, et au final, de l'ellipsoïde à un plan.

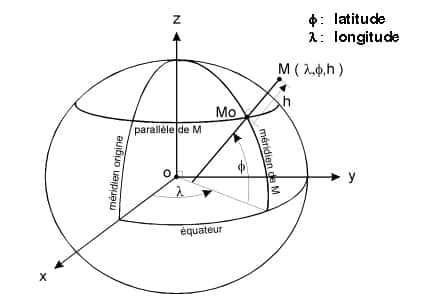
Un système de projection est une correspondance ponctuelle biunivoque entre un point de l'ellipsoïde « M0 » (voir trièdre dans Détermination d'une position par GPSGPS ci-avant) repéré par ses coordonnées géographiques (lat, long) et un point « m » du plan repéré par ses coordonnées cartésiennes planes (x, y), c'est donc un système d'équations mathématiques tel que :

M0 (φ, λ) --> m (x,y)

L'ellipsoïde n'étant pas une surface développable sur le plan, il y aura nécessairement des déformation au niveau des distance, car toutes les projections déforment les longueurs.

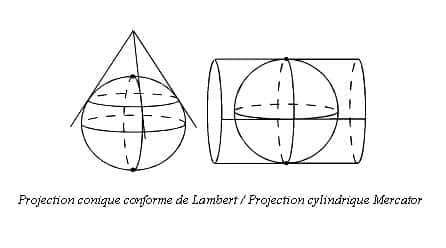
Dans la pratique, on défini une surface développable autour de l'ellipsoïde (plan, cônecône, cylindre) et on détermine une transformation amenant le point de l'ellipsoïde sur cette surface : c'est le système de projection.

Il ne s'agit pas d'une projection au sens géométrique, mais au sens mathématique.

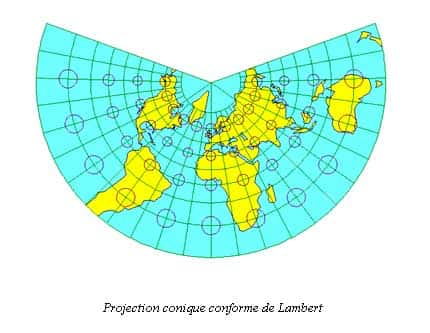
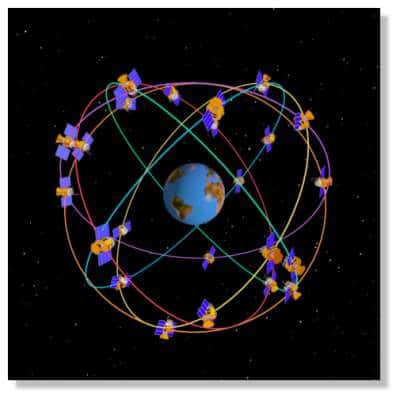
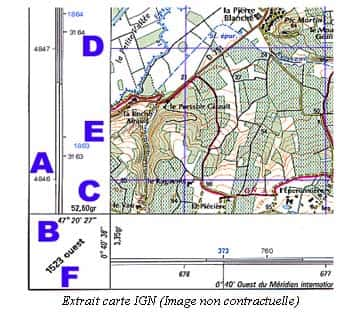
En fait, pour que l'altération des longueurs reste négligeable pour les travaux topographiques courants, la France est divisée en 4 zones du nord au sud qui ont chacune leur système de projection. La plus utilisée en France dans ces travaux est la projection LAMBERT. Il y a donc le LAMBERT I, LAMBERT II, LAMBERT III et le LAMBERT IV. Elles ont été institué par le service géographique de l'armée le 10 Août 1920 et mise en application le 15 Mars 1922. Les cartes IGN au 1/25000 et 1/50000 les utilisent.

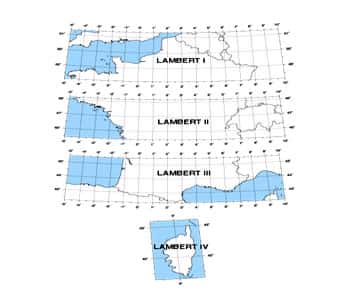
Tous les professionnels se réfèrent donc au réseau de bornes IGN, points géodésiques, dont leurs coordonnées sont exprimées dans ce système de projection LAMBERT. C'est ainsi que les cartes et plans sont tracés par les géomètresgéomètres et topographestopographes. La projection UTM (Universal Transverse Mercator) est aussi très connue et utilisée, mais plus par les cartographes.

Les récepteurs GPS les plus évolués, ceux pour les travaux topographiques, possèdent tous les transformations correspondant aux différents systèmes de projection. Ils calculent d'abord le point dans un système de coordonnées mondial, appelé WGS84, appliquent les paramètres de projection plane et fournissent un jeu de coordonnées dans le système approprié avec une projection LAMBERT ou UTM, par exemple.

On arrive donc à se retrouver sur une carte d'état major qui possède un quadrillage représentant les projections planes. Celles-ci étant exprimées en unités métriques, il est facile d'évaluer les distances sur le terrain. De plus, ses systèmes sont déterminés par un point origine O, un axe NORD (Y) et un axe EST (X). L'axe NORD est toujours exprimé comme méridien origine. En l'occurrence, le LAMBERT a pour méridien origine le méridien passant par Paris. L'UTM a pour méridien origine, le méridien de Greenwich. Ensuite, il y a le parallèle origine de l'axe EST. Pour l'UTM, c'est l'équateuréquateur et pour le LAMBERT, chaque zone a son parallèle origine (exprimé en Degrés au dessus de l'équateur):

LAMBERT I : 55°
LAMBERT II : 52°
LAMBERT III : 49°
LAMBERT IV : 46.85°

Néanmoins, les origines O du repère ne sont pas à X=0 et Y=0 car pour éviter dans certaines zones d'avoir un jeu de coordonnées négatives, on leur a donné des valeurs de départ. Par exemple, chaque zone LAMBERT à un origine O dont les coordonnées sont : X= 600 000 m et Y= 200 000 m. L'origine de l'UTM est (pour l'hémisphère nordhémisphère nord) : X= 500 000 m et Y= 0 m (exceptionnel car pour l'hémisphère sudhémisphère sud, Y= 10 000 000 m).

Tout cela pour dire que les coordonnées que vous lisez ne sont pas les distances cartésiennes directes du point à l'origine, il faut déduire la valeur de départ de l'origine.