Newton : la physique newtonienne (milieu XVIIe - XIXe siècle)

L'année même où mourait GaliléeGalilée, en 1642, naissait, le jour de Noël, l'Anglais Isaac NewtonIsaac Newton, dont l'œuvre allait être encore plus riche et révolutionnaire. Découvrez ici la physique newtonienne.

Newton toucha à tant de domaines différents qu'il fut, entre autres choses, l'inventeur d'un type de télescope, du calcul infinitésimal, de la mécanique (newtonienne) et de la première véritable théorie scientifique de la gravitation.

Qu'est-ce que la physique newtonienne ? Ici, notre planète, la Terre, et la Lune. © PIRO4D, DP

Mécanique newtonienne et lois de Newton (forces, dynamique…)

La théorie de la gravitation de Newton est principalement décrite dans notre dossier sur la relativité générale, mais il est évidemment impossible de parler de la mécanique newtoniennemécanique newtonienne sans aborder ici cette théorie.

En effet, l'un des concepts clés de la mécanique newtonienne est la « force », notion héritée de la statique (science qui étudie l'équilibre des corps immobiles) et formalisée par Newton. Or, l'exemple de force le plus immédiat dont il disposait, et qu'il utilisa naturellement, est celui de la force gravitationnelleforce gravitationnelle. Simultanément, Newton réussit ainsi à mathématiser les lois du mouvement et celle qui décrit la gravitation, validant les deux par la même occasion.

Les forces sont primordiales dans l'œuvre de Newton, car ce sont elles qui créent la dynamique. Avec Galilée, le temps avait fait son entrée dans la description du mouvement et était née la cinématique. Grâce à Newton, on assista à la naissance de la dynamique, celle-ci se distinguant de la première par le fait que le mouvement y est considéré en même temps que ses causes, ou plutôt les causes de ses modifications. En effet, pour Newton, en accord avec le principe d'inertie de Galilée et contre l'avis d'AristoteAristote, les forces ne créent pas le mouvement, mais le modifient, « l'inertie » (ou « masse inertielle ») étant la résistancerésistance naturelle des corps face aux forces. De plus, pour pouvoir énoncer ses « trois principes de la mécanique » dans ses Principes mathématiques de philosophie naturelle, publiés en 1686, Newton dut également inventer la « quantité de mouvementquantité de mouvement » et des conceptions de l'espace et du temps. Cependant, même si ces conceptions furent finalement remises en cause plus de deux siècles plus tard par EinsteinEinstein (grâce à des études, postérieures à Newton, sur les propriétés de la lumièrelumière), la quantité de mouvement évolua à peine après l'époque de Newton.

Newton énonce ses « trois principes de la mécanique » dans ses Principes mathématiques de philosophie naturelle, publiés en 1686. © DR

La quantité de mouvement¹, également nommée « impulsion » ou « moment linéaire », et souvent notée p, fut définie par Newton comme le produit de la vitessevitesse par la masse inertielle, produit dirigé le long de la première, traduisant ainsi à la fois le déplacement (par la vitesse), mais aussi l'inertie. À l'aide de ces grandeurs et de celle de force, les idées contenues dans les lois de Newton peuvent être résumées comme suit :

• « Un corps isolé, sur lequel aucune force n'agit, reste au repos ou garde la même vitesse rectiligne uniforme ». De manière équivalente, pour un corps de masse constante, on peut dire que la quantité de mouvement se conserve, ce principe de conservation de la quantité de mouvement s'étant par la suite révélé fondamental en physique.
  
  
• « Si, pendant une duréedurée infiniment courte, une force agit sur un corps, la quantité de mouvement de ce corps est modifiée, dans la direction de la force, d'une quantité égale au produit de la force par la durée ». L'accélération a étant égale à la variation de la vitesse par unité de temps, on peut montrer que cette loi s'écrit également, pour un corps de masse inertielle m constante, sous la forme plus connue (introduite par Euler en 1737) F = ma.
  
  
• « Si un corps A exerce sur un corps B une certaine force, alors le second exerce sur le premier une force de même intensité, mais de direction opposée ».

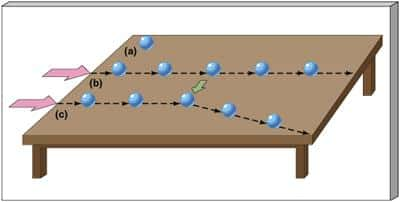
Illustration de l'influence de l'existence d'une force sur le mouvement d'un objet. En l'absence de force s'exerçant sur lui, le corps suit une trajectoire rectiligne à vitesse constante (cas b, au milieu) ; c'est le principe d'inertie. L'action d'une force (cas c) est d'influencer à la fois la direction et la valeur de la vitesse, même si le corps garde en mémoire ce qu'était sa vitesse initiale. Cela se traduit par le fait que sa trajectoire sous l'action d'une force n'est pas très éloignée de sa trajectoire libre, si la force n'est pas trop intense. © M. Bershady

La première des lois de la mécanique newtonienne est donc une reformulation claire et précise du principe d'inertie de Galilée, alors que la seconde exprime quantitativement la modification que subit le mouvement lorsque ce principe ne s'applique pas. Par ailleurs, puisqu'un mouvement non accéléré est soit le repos, soit un mouvement rectiligne uniforme, le principe d'inertie n'est qu'un cas particulier de la deuxième loi. Cette loi de la dynamique possède, de plus, une caractéristique remarquable par rapport à toutes les « lois physiques » qui existaient à cette époque.

Ainsi, contrairement aux lois de Keplerlois de Kepler, qui décrivent de manière globale le mouvement des planètes, les lois de la dynamique de Newton associées à sa loi pour la gravitation en donnent une expression locale et instantanée. Pour la première fois dans l'histoire, le mouvement n'est plus considéré dans sa globalité et la notion de causalité commence à prendre la place de celle de finalité². Toutefois, si l'on repense à ce qu'avait dit Galilée du mouvement, on remarque inévitablement un problème dans cette formulation de la mécanique qui n'est finalement (pour le moment) pas si précise que ça. En effet, contrairement à ce que croyait Aristote, le mouvement n'est pas une qualité intrinsèque des objets et ne peut être défini que par rapport à un observateur ou à un autre objet³. On peut très bien imaginer un corps qui ne subisse aucune force, mais ne reste pas au repos par rapport à un autre corps si ce dernier est mis en mouvement, et réciproquement puisque le mouvement est relatif. De plus, pour Newton, cette « inertie » des objets devait pouvoir s'expliquer pour ne pas rester une sorte de « principe mystique ». La « solution » à ces deux problèmes passait, pour Newton, par la nature de l'espace.

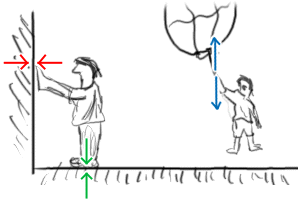
Illustrations de la troisième loi de Newton, dite « d'action-réaction ». Dans chacun des cas représentés, deux objets sont en interaction et exercent l'un sur l'autre des forces, représentées par des couples de flèches. La troisième loi de Newton stipule que, dans chaque couple, les forces sont de même intensité, mais de sens opposés. © M. Bastea-Forte, jracademy.com

L'espace et le temps newtoniens sont « absolus »

La base de la physique newtonienne est la supposition de l'existence d'un espace absolu, réceptacle de toute la matièrematière et qui lui préexiste. Plus précisément, cet espace est un espace tridimensionnel⁴ vérifiant les propriétés de la géométrie créée par EuclideEuclide. Alors que Galilée avait affirmé que « le livre de la nature est écrit dans le langage mathématique », Newton alla donc même jusqu'à décrire l'espace comme un objet mathématique. Sa mécanique allait même être si complète et efficace pour décrire les phénomènes observables que ce n'est que longtemps après l'invention des géométries non euclidiennes que l'on comprit que l'affirmation de Newton n'était pas une vérité absolue sur la nature de l'espace. Ce n'était qu'un postulatpostulat pour décrire l'objet mathématique qui modélise l'espace, et Einstein fut le premier à oser changer de postulat, même si plusieurs autres s'étaient penchés sur le sujet avant lui.

Quant à Newton, afin d'être exhaustif, il alla jusqu'à essayer de définir le temps « absolu, universel qui préside à l'ordre des choses ». L'un des mots les plus importants ici, que ce soit pour l'espace ou pour le temps, est le mot « absolu ». Il signifie à la fois que cet espace et ce temps newtoniens sont les mêmes pour tous, et également qu'ils ne sont jamais affectés par quoi que ce soit. Deux postulats qu'Einstein rejeta tour à tour. L'espace newtonien est donc un réceptacle inerte de la matière, ce qui allait exactement à l'opposé des idées d'autres, tels René DescartesRené Descartes ou Leibniz, pour qui l'espace n'existait pas « en soi », mais uniquement par la présence de matière, par son étendue⁵. Pour des raisons que nous verrons ultérieurement, Newton ne fut jamais véritablement satisfait par son espace absolu, et il lui était donc parfois assez difficile de répondre aux critiques de ses détracteurs. C'est en partie pour cela qu'il ne chercha jamais (selon ses propres mots) à « feindre des hypothèses » et essaya de s'en tenir à une description la plus neutre et objective possible, par l'intermédiaire d'équationséquations, mais aussi d'un stylestyle d'écriture sobre en rupture totale, par exemple, avec le Dialogue de Galilée.

Cependant, malgré tous ses efforts, Newton ne put concevoir une théorie quantitative, prédictive et qui explique la « nature fondamentale » des choses. Même s'il avait défini précisément ce qu'était l'espace, Newton ne réussit pas à faire mieux pour « justifier » l'inertie des corps en mouvement que d'affirmer que celui-ci était responsable de celle-là. Les corps immobiles, ou en mouvement rectiligne uniforme, le restaient, en quelque sorte, uniquement parce que l'espace, inerte, les « retient », lorsque l'on cherche à les ralentir et/ou à les accélérer. Cependant, Newton ne souhaitait initialement pas adhérer à un modèle mécaniste de l'espace, comme celui de Descartes, qui pensait pouvoir expliquer l'attraction gravitationnelle et l'inertie à l'aide de l'action d'une multitude de « tourbillonstourbillons ».

Illustration de l'univers selon Descartes. Chaque « gros corps massif » (planète ou étoile) est entouré d'un tourbillon de « fluide éthéré » responsable de l'attraction qu'exerce l'astre dominant sur les petits objets. De la même façon, le mouvement tourbillonnant est censé expliquer la répulsion entre les astres massifs, qui restent donc à distance importante les uns des autres. © DR

Critiquant le modèle de son rival et montrant son incompatibilité avec les observations (mouvement elliptique des planètes inexplicable par les tourbillons, etc.), Newton fut néanmoins forcé de reconnaître qu'il ne voyait le choix qu'entre une explication mécaniste et une explication « occulte ». Aucune des deux ne lui convenant vraiment, il resta toujours indécis. Le problème était que son espace, bien qu'absolu et doté de propriétés immuables, semblait pourtant avoir des effets physiques et ainsi une « réalité physique ». Qui plus est, si la force de gravitation n'était pas l'effet d'un « espace physique », elle était censée agir à distance entre deux corps, « par-dessus le néant », mais de manière instantanée, d'où le qualificatif « d'occulte » qui décrit parfois la notion de force.

Cette action à distance instantanée ne convenait absolument pas à Newton (et pas plus à ses détracteurs), bien que sa théorie semblât expliquer correctement le mouvement des objets célestes comme terrestres. Durant un moment, Newton espéra pouvoir décrire sa dynamique (inertie et gravitation incluses) comme l'effet d'un « bombardement » de particules sur le corps considéré. Toutefois, il comprit que cette idée n'était pas applicable et menait à des prédictions en désaccord avec les observations, même si elle préfigurait les images les plus modernes des interactions décrites à l'aide de la théorie quantique des champs. Il semble qu'au cours des dernières années de sa vie, déçu de ne pas avoir réussi à résoudre la question de la nature de l'espace et de la gravitation, Newton adhéra plutôt à l'idée de la gravitation comme étant une sorte de « principe actifprincipe actif » des corps, se rapprochant en quelque sorte d'Aristote. Chez ses successeurs en revanche, domina la conception d'un fluide subtil ayant une réalité physique qui emplissait l'espace. Une sorte d'étheréther similaire à celui qui allait être également invoqué par les théories de la lumière et ne disparaîtrait qu'avec Einstein.

Quoi qu'il en soit, supposer l'existence d'un « espace absolu » par rapport auquel sa mécanique était valable suffit à Newton pour rendre celle-ci cohérente et valide. En effet, si les lois sont valables par rapport à l'espace absolu, en utilisant la loi de compositionloi de composition des vitesses trouvées par Galilée, on montre aisément que la mécanique newtonienne doit être valide dans tous les « référentielsréférentiels inertiels » (ou « galiléens »), qui sont définis comme étant ceux en mouvement rectiligne uniforme par rapport à l'espace absolu. C'est dans toute cette classe de référentiels que les forces agissent comme le stipulent les lois de Newton, et on note que tous les référentiels inertiels étant égaux, il est impossible de définir une vitesse absolue par rapport à l'espace absolu, en accord avec le principe de relativité. Par ailleurs, si l'on souhaite étudier le mouvement d'objets par rapport à des référentiels qui ne sont pas inertiels, cette loi montre qu'il existe des effets liés à des « forces fictives d'inertie », traduisant « l'inertie du référentiel ». Ces forces d'inertie sont donc à opposer à celles qui, agissant dans les référentiels inertiels, sont des « grandeurs absolues », mais dont la définition n'est pas explicite puisqu'elle passe uniquement par leur effet dans la seconde loi.

Cependant, l'existence de forces absolues implique celle d'une accélération absolue, malgré l'absence de vitesse absolue. Newton apportait d'ailleurs une preuve de l'existence des accélérations absolues par la considération du mouvement de rotation d'un seau suspendu à une corde et rempli d'eau. Comme chacun a déjà pu le constater, l'eau en rotation est caractérisée par une surface non plane, laquelle témoigne, selon Newton, de l'existence d'une accélération absolue⁶, puisque même un observateur en rotation avec le seau la constaterait. Néanmoins, le physicienphysicien autrichien Ernst MachErnst Mach se posa la question légitime qui était de savoir ce que donnerait cette expérience réalisée dans un espace rigoureusement vide. En effet, pour Newton, le mouvement de rotation était repéré par rapport aux étoilesétoiles fixes. C'est cette distribution globale de matière qui définit l'espace absolu, et donc le repos. Si, comme le fit Mach, on imagine maintenant une situation dans laquelle ce sont toutes ces étoiles (l'universunivers) qui seraient en rotation, le seau restant au repos, on serait dans une situation où seule une accélération relative existerait pour le seau, et la surface de l'eau devrait donc rester plane selon Newton. Pour Mach, cela n'avait aucun sens et l'on devait imaginer que, dans la seconde situation, le seau subirait une force similaire provoquée par le « mouvement global de l'univers », ce qui invaliderait le concept d'accélération absolue et expliquerait l'inertie comme une sorte d'effet moyenné de l'existence du reste de l'univers. Dans un espace rigoureusement vide, Mach prévoyait donc que la rotation serait sans effet, car indiscernable. Toutefois, cette question assez subtile (en fait déjà évoquée par Berkeley au XVII^e siècle) resta en suspens jusqu'à ce que naisse la relativité généralerelativité générale, et cela n'empêcha pas la mécanique newtonienne de devenir, grâce à la « recette » précédente, un outil robuste et fiable que personne ne remettrait en cause avant fort longtemps.

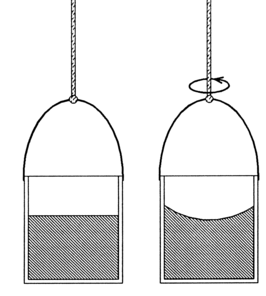
À l'intérieur d'un seau à l'équilibre statique dans un référentiel inertiel, la surface de l'eau est plane (figure de gauche). C'est une conséquence de la mécanique newtonienne appliquée aux fluides. Une autre prédiction de celle-ci est que, si le seau est, dans ce même référentiel inertiel, en rotation uniforme autour d'un axe vertical (figure de droite), la surface de l'eau ne sera plus plate, mais parabolique. Selon Newton, ceci s'explique par l'apparition de « forces fictives d'inertie », le seau n'étant pas un référentiel inertiel. Toutefois, selon ce même principe, si l'ensemble des étoiles lointaines, grâce auxquelles on repère le mouvement du seau, se mettait en rotation autour du seau, la surface de l'eau resterait plane. Pour Mach, il doit y avoir symétrie entre les deux situations, et une rotation de l'ensemble des étoiles doit, selon lui, également impliquer une courbure de la surface de l'eau. Pour Newton, il existe des accélérations absolues par rapport à un référentiel inertiel, pour Mach il ne doit exister que des accélérations relatives. © DR

Applications et succès de la mécanique newtonienne (découverte de Neptune…)

Avant d'aller plus en avant dans les réussites et développements de la théorie newtonienne dans les siècles qui suivirent, il est important d'insister sur un point qui pourrait passer inaperçu de nos jours et qui est lié au rôle majeur de la gravitation dans l'élaboration de la mécanique newtonienne. Si Newton se permit de parler « d'espace absolu réceptacle de toute chose », c'est qu'il avait compris que la séparationséparation faite par Aristote entre « monde sensible » et « monde céleste » n'avait pas lieu d'être.

Pour un esprit moderne habitué à voir des photos d'autres planètes prises par des sondes que l'on a envoyées jusque là-bas (en utilisant, entre autres choses, les lois de la mécanique de Newton), cela peut sembler une évidence. Pourtant, Newton fut le premier à oser affirmer haut et fort que ces deux mondes n'en faisaient qu'un, même si les observations astronomiques faites par Galilée de la LuneLune et du SoleilSoleil avaient déjà entamé la « matérialisationmatérialisation » des objets célestes. Pire que tout, Newton osa même le prouver en donnant une loi quantitative qui rende parfaitement compte des mouvements célestes et de la chute des corps. À une époque où nombre de « philosophes naturels », parmi les plus brillants, se contentaient bien souvent de mentionner des explications qualitatives, c'était un véritable exploit, et ce d'autant plus que Newton dut même inventer les outils mathématiques sur lesquels reposerait sa théorie, outils qui débouchèrent sur le calcul différentiel et sur le calcul intégral.

Lorsque parurent les Principes de Newton, le succès fut immédiat en Angleterre. En effet, Newton résolvait dans son ouvrage le problème de la gravitation, sur lequel nombre de ses collègues séchaient depuis plusieurs mois, tout en illustrant par plusieurs exemples comment sa théorie fonctionnait et ce qu'elle prédisait : la forme des trajectoires des comètescomètes, les maréesmarées, etc. Cependant, la mécanique newtonienne et la théorie de la gravitation universelle ne furent pas acceptées du jour au lendemain à l'étranger, où elles eurent parfois de farouches adversaires, parmi lesquels Descartes et Leibniz. Néanmoins, malgré ces derniers, les confirmations observationnelles et expérimentales étaient bien là : Descartes prévoyait, avec sa théorie des tourbillons, que la Terre était en rotation autour de son plus long axe. Or, Newton prévoyait le contraire, et c'est ce qui fut vérifié par Pierre-Louis de Maupertuis, qui observa un aplatissementaplatissement de la Terre aux pôles en 1736. Peu après, Edmond HalleyEdmond Halley prédit, grâce à la théorie de Newton, et avec une très grande précision, le retour en 1758 de la fameuse comète qui porteporte depuis son nom.

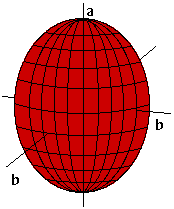
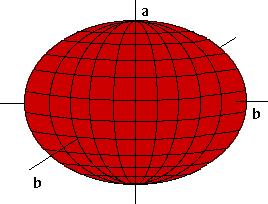
En haut, la forme de la Terre du fait de sa rotation selon Descartes. En bas, la forme selon Newton. La forme réelle de la Terre est plus proche de celle prévue par Newton, même si la déformation réelle ne serait pas visible à l'œil nu sur une telle figure. © The Math Forum

De plus, même si développée et adaptée, la mécanique de Newton fut rapidement capable de décrire le comportement des fluides comme celui des solidessolides ; l'une de ses réussites les plus flagrantes eut lieu en 1846. Cette année-là, Le Verrier et Adams prédirent indépendamment l'existence et la position d'une nouvelle planète, sur la simple foi des lois de Newton et du non-respect de celles-ci par UranusUranus. Grâce à ces lois, ils montrèrent par le calcul que l'existence de NeptuneNeptune perturbait la trajectoire d'Uranus et expliquait parfaitement les observations. Neptune fut trouvée exactement là où ils le prédisaient, au moment auquel ils le prédisaient. C'est pourquoi, lorsque l'on observa que MercureMercure se comportait d'une manière un peu différente de ce que prévoyait la théorie de Newton, le premier réflexe fut non pas de douter de celle-ci, mais de supposer l'existence de corps astrophysiquesastrophysiques inconnus (voir par exemple le livre d'Eisenstaedt pour plus de détails). Comme plusieurs fois dans l'histoire, ce qui semblait n'être qu'une petite anomalieanomalie allait déboucher sur une révolution, puisque seul Einstein fut capable d'expliquer quantitativement cet effet, grâce à sa théorie de la relativité générale, qui reniait, entre autres, la théorie newtonienne de la gravitation. Cependant, Einstein dut auparavant éclaircir une anomalie bien plus importante liée à l'éther et à la propagation de la lumière, ce qu'il fit par une remise en cause complète de l'autre grande œuvre de Newton : sa mécanique.

Notes :

1 Cette expression, qui n'a pas d'équivalent anglophone, semble due à Descartes.

2 On peut noter que, de manière a priori assez surprenante, le concept de finalité redevint à la mode grâce aux formulations variationnelles d'Hamilton et Lagrange de la mécanique. Sans parler de l'importance de celles-ci dans le cadre quantique.

3 Dans le vocabulaire moderne de la physique, un « observateur », ou un « objet », par rapport auquel on mesure des grandeurs physiques est communément nommé un « référentiel ».

4 Dans un espace à trois dimensions, trois nombres sont nécessaires pour repérer un objet par rapport à un autre de manière unique. Par exemple, par rapport à la surface de la Terre, la longitudelongitude, la latitudelatitude et l'altitude. Ou bien, à l'intérieur d'une pièce rectangulaire, les distances par rapport à deux mursmurs perpendiculaires et celle par rapport au sol ou au plafond.

5 Assez ironiquement, Einstein partageait les idées de Descartes et Leibniz, mais sa théorie de la relativité générale est plus en accord avec la conception de Newton, puisque, dans le cadre de la relativité générale, un univers dynamique est possible même en absence de toute matière.