au sommaire
Plongez ici dans le monde de GaliléeGalilée (1564-1642), connu pour son étude détaillée de la chute des corps, mais aussi pour sa lunette astronomique, ainsi que pour son principe d'inertie. Surtout, découvrez comment, avec Galilée, le mouvement devint relatif (le mouvement n'existe que par rapport à quelque chose).
Bien souvent, on connaît avant tout la façon dont Galilée défendit le système copernicien devant l'Église. Par ailleurs, même si l'influence qu'eurent sur Galilée divers scientifiques de la fin du Moyen Âge français, tels Jean Buridan et Nicolas Oresme, est encore un sujet de discussion, il semble que Galilée fut l'initiateur de la cinématique et de la dynamique modernes.

Découvrez comment, avec Galilée, le mouvement devint relatif. Ici, la Voie lactée vue depuis un site d'observation au Chili. © Y. Beletsky (LCO), ESO, CC by 4.0
En effet, chez AristoteAristote, la notion de temps était absente de celle de mouvement. Le mouvement, propriété intrinsèque des objets, était uniquement spatial, entièrement décrit par une trajectoire et une finalité. Avec Galilée, le mouvement devint une propriété relative et naquirent les notions toujours actuelles de vitesse instantanée (variation de la position avec le temps) et d'accélération (variation de la vitesse avec le temps).

Disciple et fervent admirateur d'Aristote, l'Italien Galileo Galilei, dit Galilée, est plutôt perçu comme le premier à avoir remis en cause son enseignement. © DR
Galilée, la chute des corps et l'expérience de la tour de Pise
La cinématique de Galilée commença, vers 1590, par l'étude détaillée de la chute des corps et, plus généralement, la cinématique des corps libres. Suivant les préceptes d'Aristote, dont il se déclarait lui-même le disciple, Galilée observa la nature en quête d'explications simples. Il vérifia ainsi que des objets de masses différentes chutent identiquement (contrairement à ce qu'affirmait Aristote), et alla jusqu'à quantifier l'évolution temporelle de cette chute libre, la décrivant comme « continûment et uniformément accélérée », ce qui marqua réellement la naissance de la cinématique1.
D'ailleurs, selon une légende souvent répétée, Galilée aurait volontairement laissé tomber des objets depuis le haut de la tour penchée de Pise pour tester son hypothèse. On doute aujourd'hui sérieusement de la véracité de cette histoire, mais on sait en revanche avec certitude que Galilée fit de nombreuses expériences avec des boules roulant sur des plans d'inclinaisons variables, expériences qui le menèrent à énoncer le principe d'inertie (voir plus loin), qui porteporte désormais son nom.
En ce qui concerne la chute libre et la pesanteur, il fallut attendre Newton et la deuxième moitié du XVIIe siècle pour plus d'études et une explication de la loi empirique découverte par Galilée. Toutefois, comme Newton plus tard, Galilée ne se contenta pas d'apporter d'importantes contributions à la cinématique.

Illustration de l'expérience sur la chute des corps que, selon la légende, Galilée aurait faite du haut de la tour de Pise. © Paul G. Hewitt, Conceptual Physics, 1981
Galilée, la lunette astronomique et les satellites de Jupiter
En 1604, fut faite une observation qui allait bouleverser non seulement la vie de Galilée, alors âgé de 40 ans, mais également la science contemporaine et à venir. Une « nouvelle étoileétoile », visible à l'œilœil nu, fut soudain remarquée dans la constellationconstellation du Sagittaire. Objet de nombreuses discussions, cette supernovasupernova (la dernière en date dans notre GalaxieGalaxie) fut soigneusement étudiée par Johannes KeplerJohannes Kepler et attira l'attention de Galilée sur l'astronomie.
Il eut ainsi connaissance du modèle héliocentriquehéliocentrique de Nicolas CopernicCopernic et commença lui-même à faire de nombreuses observations astronomiques. Cependant, la qualité de ses observations augmenta très sensiblement à partir de 1610. En effet, en 1609, il entendit parler des lunettes d'approche que vendaient les forains en Hollande, ce qui lui inspira l'idée de se faire construire une lunette sur le même principe, mais dédiée à l'astronomie.
L'effet de cet instrument, qui grossissait 32 fois, ne se fit pas attendre : dès janvier 1610, Galilée découvrit les quatre plus gros satellites de JupiterJupiter. Ce n'était que le début d'une longue série de découvertes qui allaient révolutionner notre conception de l'universunivers et finir de convaincre Galilée de la validité du modèle héliocentrique. Entre autres choses, il observa ainsi le relief accidenté de la LuneLune, les taches solairestaches solaires, la Voie lactéeVoie lactée composée d'étoiles, et également les phases de MercureMercure et de VénusVénus, prédites par les partisans de Copernic.
Galilée, son Dialogue sur les deux grands systèmes du monde et son procès
Toutefois, avec la publication à partir de 1613 de ces observations, Galilée commença à se faire de sérieux ennemis au sein de l'orthodoxie romaine. Une plainte fut déposée contre lui au Saint-Office, et, malgré ses arguments scientifiques, il ne put défendre le système copernicien. En 1616, l'œuvre de Copernic fut mise à l'index et Galilée officiellement sommé de changer de sujets d'études. Quelques années plus tard, le temps passant et un nouveau pape ayant été élu en 1623, Galilée se crut à l'abri et publia en 1632 son Dialogue sur les deux grands systèmes du monde. Ce Dialogue allait être à l'origine d'un des procès les plus célèbres de l'histoire.
En effet, comme l'indique le titre, cet ouvrage retranscrit un imaginaire dialogue dont le sujet principal est la comparaison entre les modèles géocentriquegéocentrique (hérité de PtoléméePtolémée et Aristote) et héliocentrique (hérité d'Aristarque de Samos et Copernic) du monde. Les trois protagonistes sont un partisan de chacun des systèmes, plus un honnête homme sans préjugé. Dans un stylestyle inspiré de Platon, Galilée procède à une maïeutique, poussant apparemment le partisan d'Aristote dans ses contradictions. Suite à cet ouvrage, Galilée fut convoqué au tribunal, condamné par l'Inquisition en 1633 et contraint à « abjurer, maudire et récuser » ses erreurs passées. Évènement à la suite duquel une autre légende naquit autour de Galilée : celle selon laquelle après avoir obéi, il aurait murmuré (ou se serait écrié) « Eppur, si muove ! » (« Et pourtant, elle se meut »).
Quoi qu'il en soit, après son procès, au cours duquel il se défendit à peine, Galilée, physiquement diminué, se retira dans sa villa près de Florence. Suite aux nombreuses observations solaires qu'il avait faites, il devint complètement aveugle à partir de 1637, ce qui ne l'empêcha pas, en compagnie de son disciple Evangelista TorricelliEvangelista Torricelli, de continuer à travailler et d'approfondir sa dynamique jusqu'à sa mort en 1642. En 1638, fut d'ailleurs publié son Discours sur deux sciences nouvelles à l'intérieur duquel sont résumées ses dernières réflexions au sujet de la dynamique.
La relativité galiléenne et le principe d'inertie
Toutes les théories scientifiques naissent, grandissent, atteignent un âge de maturité et parfois meurent (ou se retrouvent incluses dans une théorie plus vaste). La relativité galiléenne et le principe d'inertie n'ont pas échappé à cette loi, et la naissance de ces deux grands piliers de la cinématique ne fut pas aussi nette qu'on le laisse souvent croire. Ainsi, on a même longtemps débattu pour savoir si Galilée avait bel et bien énoncé le principe d'inertie. Le but principal ici étant d'essayer d'expliciter ces deux lois de la physiquephysique afin de mieux cerner la théorie d'EinsteinEinstein, nous allons éviter pour un moment la plupart des détails historiques. Seule une compilation du contenu des deux ouvrages de Galilée, le Dialogue et son approfondissement, le Discours, sera donnée par la suite. Le premier est grossièrement une présentation de la relativité galiléenne, alors que dans le second ouvrage, on trouve à la fois une analyse plus poussée de celle-ci et ce qui ressemble le plus, dans l'œuvre de Galilée, à un énoncé du principe d'inertie.
Dans le Dialogue, la majeure partie de la conversation concerne ce qui se passe à l'intérieur d'un navire qui se déplacerait à vitesse constante. Entre autres exemples, Galilée imagine des papillons voletant à l'intérieur d'une cabine ou un boulet tombant du haut d'un mât. Comme il le fait remarquer, « pourvu que le mouvement soit uniforme et ne fluctue pas », le vol de papillons ou la chute du boulet par rapport au navire se déroulent comme si celui-ci était à quai. Autrement dit, sans repères extérieurs, rien ne permet de distinguer un mouvement à vitesse uniforme de l'immobilité : « le mouvement est comme rien ». Cette simple phrase résume l'essence du principe de relativité et renie complètement les principes d'Aristote selon lesquels le mouvement et le repos sont deux concepts complètement différents puisque le premier était censé altérer la constitution interne des objets.
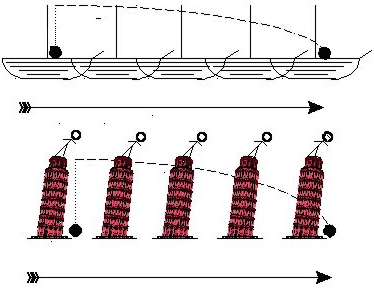
Illustration du principe de relativité de Galilée : la chute libre d'un corps se produit de manière strictement verticale, qu'elle ait lieu par rapport à un repère fixe (corps lâché du haut de la tour de Pise) ou sur un bateau en mouvement uniforme. De même, un observateur en mouvement par rapport à la tour, ou bien immobile par rapport à la berge le long de laquelle se déplace le navire, verra les objets en chute libre suivre deux trajectoires identiques. Le mouvement est relatif et la physique est la même pour tous les observateurs inertiels (ou galiléens). © Stanford Encyclopedia of Philosophy
Avec Galilée, le mouvement devient relatif : il n'existe que par rapport à quelque chose, c'est une propriété qui dépend de l'observateur et peut donc être partagée, conduisant alors à un repos relatif. De cette façon, même s'il n'argumentait pas directement en faveur du modèle de Copernic, Galilée détruisait au moins l'argument de Ptolémée contre le mouvement de la Terre.
De plus, poussée un peu plus loin, sa réflexion l'amena à établir la loi de compositionloi de composition des vitesses en mécanique classique : si un papillon se déplace à la vitesse v par rapport à un bateau qui navigue à la vitesse w par rapport à la terre ferme, la vitesse du papillon par rapport à la terre ferme est v+w. On verra plus tard comment cette loi si simple fut mise à mal par la lumièrelumière à la fin du XIXe siècle.
Toutefois, à la lecture du Dialogue, on peut légitimement se demander comment un tel principe est possible, s'il n'y a pas de contact physique entre les corps. En effet, imaginons des papillons initialement posés sur le sol du navire en mouvement. Pour que les papillons volettent à l'intérieur du navire comme si celui-ci était à quai, il faut qu'ils gardent la même vitesse que lui par rapport au quai, même lorsqu'ils décollent et ne sont plus entraînés par le plancherplancher. Ceci est le principe d'inertie : le mouvement est « imprimé de façon indélébile » dans les corps, dès lors qu'ils sont mis en mouvement. Nul besoin, contrairement à ce que prétendait Aristote, que des « forces » s'exercent pour maintenir les objets à vitesse constante. Notons que Galilée fut probablement amené à le découvrir en faisant rouler des boules sur des plans de plus en plus proches de l'horizontale, et qu'il déduisit ce principe alors que chacun peut très facilement constater dans le monde réel que les choses ne se passent pas ainsi : tout objet lancé finit par s'arrêter.
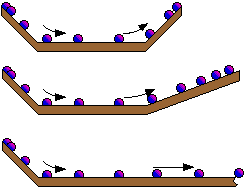
Illustration du principe d'inertie à l'aide de billes roulant librement sur des plans d'inclinaisons variables. Dans chacun des cas, une bille est abandonnée sans vitesse initiale en haut à gauche. Une fois arrivée en bas du plan incliné gauche, elle est dotée d'une certaine vitesse. Si, continuant son chemin, elle rencontre un autre plan incliné, mais qui monte, elle finira par s'arrêter (comme dans les deux premiers exemples). Cependant, si la pente est moins forte (deuxième cas comparé au premier), la bille pourra aller plus loin, atteignant toutefois une altitude égale à son altitude initiale. Le cas extrême est celui où le plan est horizontal (troisième cas), situation dans laquelle la bille roulera indéfiniment à vitesse constante, si rien ne s'oppose à son mouvement. C'est le principe d'inertie découvert par Galilée. © N. Alberding
Le génie de Galilée fut donc ici d'avoir su voir au-delà des apparences et d'avoir compris que « le mouvement se conserve », même si, dans le monde réel, de nombreux parasitesparasites forcent les objets en mouvement uniformemouvement uniforme à ne pas le rester. Pour certains, Galilée a, en quelque sorte, perçu la « vérité mathématique » (au sens platonique) derrière les apparences trompeuses du monde.
Cependant, ce que dit Galilée de ce principe d'inertie n'est aucunement une explication de la raison pour laquelle le mouvement reste « imprimé ». De plus, dans sa formulation de ce principe, il introduisit, à tort, le besoin d'une surface horizontale pour que la vitesse persiste, besoin qui semble résulter dans son esprit des expériences qu'il fit avec des boules roulant sur des plans de plus en plus horizontaux.
Ainsi, malgré ses réflexions sur les papillons volant à l'intérieur d'un bateau, et en contradiction avec celles-ci, Galilée n'imaginait pas qu'un corps sans contact avec quoi que ce soit garde une vitesse constante. Il fallut attendre René DescartesRené Descartes et Robert Hooke pour que le principe soit proprement formulé, alors que Newton fut celui qui éclaircit la notion d'inertie, en tant que capacité à résister à la mise en mouvement.
Par ailleurs, il y a un autre point important à signaler. Pour Galilée, les corps en mouvement uniforme persistaient dans cet état uniquement car ce mouvement se faisait à la surface de la Terre. Celle-ci étant ronde, ils avaient alors un mouvement circulaire uniforme, le seul qui soit, selon Aristote, véritablement « naturel ». Cette hypothèse de préférence du mouvement circulaire uniforme, qui était contredite par les observations et calculs de Kepler mais reprise par Galilée, illustre le fait que ce dernier n'avait pas complètement pris son indépendance vis-à-vis d'Aristote. Newton, « hissé sur les épaules des géants qui l'ont précédé », sut voir plus loin et devint le « premier physicienphysicien moderne », même s'il fut également le dernier à avoir cherché une « science théologique ».
Note :
1 On définit la cinématique comme l'étude descriptive du mouvement qui ne se préoccupe pas des causes de celui-ci, par opposition à la dynamique, qui étudie quantitativement le mouvement et ses causes.