au sommaire
- À lire aussi
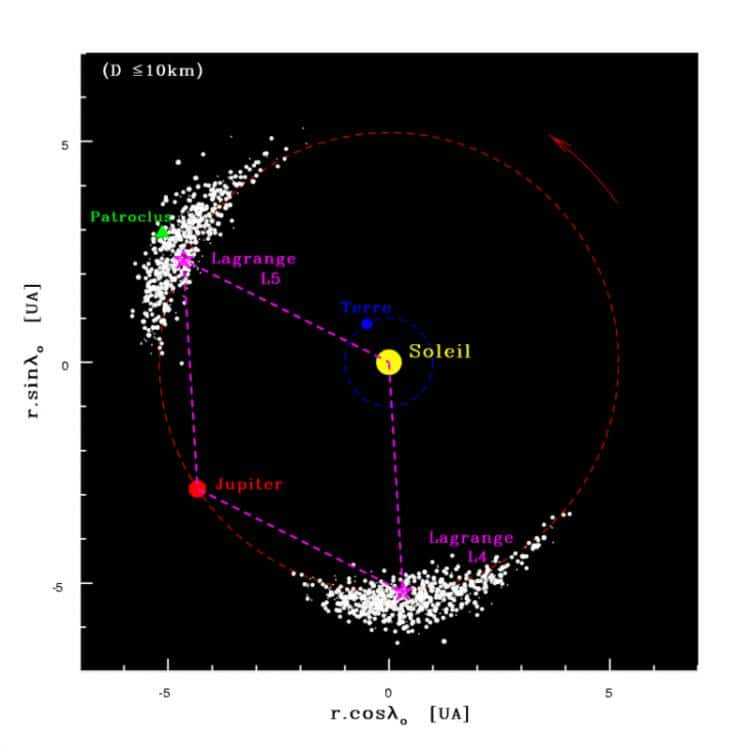
Vue du système des troyens de Jupiter dans le plan de l'écliptique. Patroclus fait partie du groupe des "grecs" associé au point d'équilibre de Lagrange L5. Crédit : IMCCE/OP/CNRS
Lorsque qu'on cherche à décrire le comportement de deux électrons en orbite autour d'un noyau à l'aide de l'équation fondamentale de la mécanique quantique découverte en 1926 par Erwin Schrödinger, on résout une équation décrivant la propagation d'une onde, non pas dans l'espace, mais dans un espace de configurations à 6 dimensions, celle des positions des particules. Schrödinger en était bien conscient mais il pensait malgré tout que les ondes de matière postulées par de Broglie, et dont il était parti pour développer sa mécanique ondulatoiremécanique ondulatoire, devaient malgré tout être des densités de charges électriques oscillant et interférant à la manière des ondes à la surface d'un bac à eau dans lequel on aurait jeté une pierre.
Les électrons en orbite devaient donc être des paquetspaquets d'ondes de ce champ de densité électrique, se déplaçant à la façon des rayons lumineux dans un milieu d'indice donné. De cette manière, les mystérieuses propriétés ondulatoires de la matièrematière pouvaient être réconciliées avec ses indiscutables propriétés corpusculaires, parfaitement évidentes lorsque l'on considérait le mouvementmouvement d'une particule chargée dans l'ancêtre des chambres à bulles, les chambres de Wilson.
Il ne tarda pas à déchanter. La déconvenue vint de ses échanges épistolaires avec Hendrik Lorentz, le grand théoricien hollandais à l'origine de l'introduction de la forme moderne des équations de Maxwelléquations de Maxwell, tenant compte de la théorie cinétique des gazgaz appliquée aux électrons découverte par Thompson. Les deux chercheurs parvinrent à la conclusion que tout paquet d'onde bien localisé, décrit par l'équation de Schrödingeréquation de Schrödinger représentant un électron en orbite dans le champ coulombien électrostatiqueélectrostatique d'un noyau, devait finir par se disperser.
Au même moment, Max BornMax Born, à qui l'on devait la formulation matricielle précise de la mécanique quantique découverte initialement par Werner HeisenbergWerner Heisenberg, arriva à la conclusion que le scalaire de champ introduit par Schrödinger, ce que nous appelons aujourd'hui la fonction d'onde d'un électron, trouvait son interprétation non en tant que densité de charge mais en tant qu'amplitude de probabilité de trouver un quanta de matière en un point de l'espace de configuration. Il était parvenu à cette conclusion en cherchant à décrire l'expérience de diffusiondiffusion des particules alpha par des noyaux, c'est-à-dire la fameuse expérience de Rutherford.

Erwin Schrödinger. Crédit : th.physik.uni-frankfurt
L'image d'un paquet d'onde stable bien localisé pour décrire le mouvement d'un électron dans un atomeatome vient pourtant d'être en partie ressuscitée à la suite d'une récente expérience décrite dans un article de Physical Review Letters dont les auteurs sont H. Maeda (Japan Science and Technology Agency, Tokyo), J. H. Gurian, TT. F. Gallagher (université de Virginie).
Il faut savoir que malgré l'échec des tentatives de Schrödinger et Lorentz, on ne pouvait pas faire complètement l'impasse sur une notion d'orbite d'une particule pour décrire l'intérieur d'un atome. Comme Sommerfeld l'avait montré, on obtient une description plus précise du spectrespectre d'un atome si l'on introduit dans le modèle de Bohrmodèle de Bohr non pas des orbites circulaires mais des orbites elliptiques, comme dans le cas des planètes du système solairesystème solaire.
En fait, la découverte même de la mécanique des matrices par Heisenberg reposait sur l'utilisation des méthodes mathématiques avancées de la mécanique céleste avec les développements multipériodiques en séries de Fourier. Pas étonnant donc que Schrödinger ait été attaché à l'idée d'une représentation somme toute assez classique du mouvement d'un électron dans un atome.
Or, il existe en mécanique céleste un phénomène bien connu et découvert mathématiquement par Lagrange au dix-huitième siècle. Lorsque l'on considère deux corps, comme le SoleilSoleil et la Terre ou JupiterJupiter et le Soleil, il existe 5 points particuliers entraînés par la rotation d'un des deux corps. Il s'agit de valeurs extrêmes relativement à la combinaison des forces de gravitationforces de gravitation et de Coriolis dans le référentielréférentiel tournant autour du corps principal.
Deux de ces points sont stables. Un corps céleste, comme un astéroïdeastéroïde, s'y retrouve piégé et peut tout au plus effectuer autour de ces points des mouvements selon des trajectoires fermées. Il s'agit des célèbres points de Lagrangepoints de Lagrange L5 et L4.
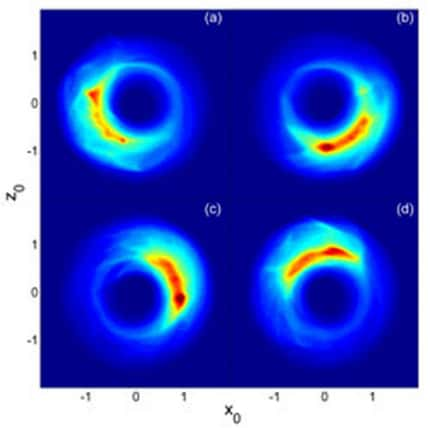
Remarquablement, le physicienphysicien Bialynicki-Birula avait prédit avec quelques collègues en 1994 que si l'on soumettait l'électron d'un atome de Rydbergatome de Rydberg à une onde électromagnétiqueonde électromagnétique polarisée circulairement, de telle sorte qu'elle soit synchronisée avec la période de cet électron sur son orbite, des points de Lagrange similaires devaient apparaître. Un électron sous forme initialement d'un paquet d'ondes bien localisé placé en ces points de Lagrange le restera donc.
L'expérience vient d'être réalisée avec des atomes de lithiumlithium ionisés. C'est un résultat remarquable qui montre une fois de plus qu'il faut se méfier des domaines de la physiquephysique qui semblent parfaitement explorés et maîtrisés. Pour un chercheur débutant, c'est heureux...