au sommaire
La société canadienne D-Wave Systems a très probablement marqué des points en direction de la réalisation de calculateurs quantiquescalculateurs quantiques performants. Mais il ne s'agit pas encore d'ordinateursordinateurs dans le sens précisé par Alan TuringAlan Turing et John Von NeumannJohn Von Neumann. C'est-à-dire que ce ne sont pas encore des machines sur lesquelles il est possible d'exécuter n'importe quel programme. Des outils qui sont spécifiques à la résolutionrésolution de problèmes spécifiques demeurent, comme de simuler certains systèmes quantiques en chimie et en physique du solide qui restent difficiles à analyser avec des ordinateurs classiques. Mais au fond, c'est probablement ce que Feynman avait avant tout en tête lorsqu'il a commencé ses travaux de pionniers dans le domaine des ordinateurs quantiques.
A l'instar des ordinateurs classiques, ces machines doivent manipuler des bits d'informations. Mais comme elles doivent exploiter le phénomène de superposition des états quantiques et faire intervenir celui d'intricationintrication, il est question de qubits. Le problème principal des ordinateurs quantiques est celui de la décohérence et il n'est pas assuré du tout qu'il soit résolvable.
Pour être efficace, un ordinateur ou un calculateur quantique doit permettre de manipuler un grand nombre de qubits qui se trouvent dans un état qui ressemble à celui d'un crayon en équilibre à la verticale sur sa pointe. En poursuivant l'analogieanalogie, il faut donc, en quelque sorte, opérer sous vide et en l'absence de toutes perturbations issues de l'environnement extérieur, sans quoi le crayon tombe.
Le prix Nobel de physique David Wineland et ses collègues du National Institute of Standards and Technology (NISTNIST) à Boulder, dans le Colorado (USA), qui travaillent sur ce problème, pensent que l'une des voies les plus prometteuses consiste à utiliser des qubits sous forme de moments cinétiques particuliers, c'est-à-dire de spinsspins, portés par des ionsions. Ils ne sont pas les seuls. D'autres groupes de recherche sur la Planète font de même comme l'Ion TrapTrap Quantum Computing Group de l'université d'Oxford (UK).

Le prix Nobel de physique David Wineland est un des pionniers des expériences sur la décohérence quantique. Il explore la voie des pièges à ions pour réaliser des ordinateurs quantiques. © NIST
Des portes logiques connectées à des mémoires quantiques
Dans tous les cas de figure, un ordinateur quantique doit posséder plusieurs composants avec des fonctions bien spécifiques. Il faut par exemple un ensemble de portesportes logiques élémentaires qui permettent ensuite d'effectuer tous les calculs et tous les algorithmes que l'on veut. Mais il faut aussi des mémoires.
Cela fait déjà un certain temps que les physiciensphysiciens, notamment ceux du NIST, savent réaliser ces composants en intriquant des ions. Mais il s'agissait toujours des mêmes. Or il se trouve qu'il est concevable d'améliorer les performances en choisissant des ions différents et, surtout, en intriquant des ions différents entre eux. Cette dernière possibilité vient d'être réalisée pour la première fois et indépendamment par les deux groupes qui l'ont annoncé dans deux articles publiés dans le journal Nature (en accès libre sur arxiv). Le groupe du NIST a intriqué un isotopeisotope de bérylliumbéryllium 9 avec un isotope de magnésiummagnésium 25 alors que celui d'Oxford a utilisé des isotopes de calciumcalcium 40 et de calcium 43.
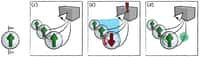
Pour tester la réalité de l'intrication, les deux groupes ont utilisé l'inégalité de Bell. En mesurant le spin de l'une des particules intriquées dans une paire puis celui de la seconde, il apparaît des corrélations dans les mesures obtenues qui sont décrites par des lois des probabilités. Bien que ces corrélations ne puissent pas servir à faire du morsemorse pour transmettre un message, elles montrent que l'état de l'une des particules est affecté par un changement dans celui de l'autre à une vitessevitesse supérieure à celle de la lumière. L'inégalité que Bell a découverte découle de ce phénomène qui est proprement quantique et signal sans l'ombre d'un doute, l'occurrence de l'intrication. Elles doivent apparaître comme violées dans les expériences de mesures de spins pour des paires intriquées.
Tel a bien été le cas dans les expériences menées par les chercheurs.