au sommaire
Albert EinsteinEinstein n'a jamais été satisfait de l'interprétation orthodoxe de la mécanique quantique avancée par Bohr, Heisenberg, Dirac et Born. Pourtant, il était très bien placé pour comprendre la mécanique quantique puisque ses travaux ont été à l'origine de ceux d'Heisenberg, de Broglie et Schrödinger. On simplifie souvent sa position en disant qu'il était incapable d'accepter l'apparition des probabilités en physique quantique et qu'il ne voulait pas renoncer au déterminisme.
En fait, Einstein a été le premier à introduire le calcul des probabilités en mécanique quantique avec sa théorie des transitions dans l'atome de Bohr. C'est cette théorie qu'Heisenberg va prendre pour base pour découvrir sa mécanique matricielle. Einstein n'était donc pas foncièrement opposé à l'usage des probabilités en physique quantique, mais comme il l'a fait remarquer dans une lettre à Pauli paraphrasant Caton l'Ancien : « Je ne dis pas probabilitatem esse delendam, mais probabilitatem esse deducendam, ce qui est très différent ».

De gauche à droite, les auteurs du fameux paradoxe EPR, Albert Einstein, Boris Podolsky et Nathan Rosen. L'article qu'ils ont publié ensemble en 1935 a révélé le phénomène de l'intrication quantique. © DP
Le paradoxe EPR et les inégalités de Bell
Pour Einstein, les vraies lois de la physique quantique devaient permettre de comprendre pourquoi l'utilisation du calcul des probabilités pour comprendre les orbitales atomiques était une nécessité. Il était sans doute aussi profondément insatisfait du conflit entre les conceptions de l'espace et du temps selon la mécanique quantique et selon sa théorie de la relativité générale. Anticipant sans doute les problèmes que l'on allait rencontrer en tentant de construire une théorie quantique de la gravitation, il refusait donc de croire que les équations découvertes par Heisenberg, Born, Schrödinger et Dirac représentaient la solution définitive à l'énigme des quanta de lumièrelumière.
C'est sans doute en raison de toutes ses considérations qu'Einstein a été conduit à découvrir le fameux paradoxe EPR. Pour lui, ce phénomène, que l'on sait profondément lié à la notion d'intrication quantiqueintrication quantique, devait signifier qu'il devait probablement exister des variables cachées qui, si elles étaient connues, non seulement permettraient de donner une meilleure solution, plus complète, à l'énigme quantique, mais aussi restaurerait un déterminisme fondamental.

Dans les années 1960, le physicien John Bell, ici dans son bureau du Cern, a découvert qu'un test permettait de départager Einstein et Bohr dans le cas de certaines alternatives à la théorie quantique orthodoxe. À l'époque, la technologie ne pouvait pas encore suivre, mais dans les années 1970, tout a changé. En 1982, Alain Aspect et ses collègues purent réaliser une expérience importante faisant pencher lourdement la balance en faveur de Bohr. © Cern
On sait que les inégalités de Bell, et surtout l'expérience d'Alain Aspect qui a permis de les tester, ont renforcé le point de vue de l'école de Copenhague. Les nombreux articles consacrés à des expériences sur l'effet EPR, menées parfois afin de tester d'une nouvelle façon les inégalités de Bell, répètent ad nauseam que ces expériences donnent raison à Bohr et tort à Einstein dans la mesure où elles excluent les théories à variables cachées dites locales. En fait, à rigoureusement parler, cela est faux, et personne n'en a jamais fait mystère dans la communauté scientifique, même si cela n'est pas très bien connu du public cultivé.
Les trois points faibles des tests avec photons intriqués
En effet, les expériences menées avec des paires de photons intriqués possèdent trois points faibles. Une réfutation imparable des théories locales supposerait une expérience ne comportant aucun de ces points faibles. On cherche à en réaliser une depuis longtemps, mais sans succès pour le moment. Les chercheurs ont pu remédier à au moins l'un des points faibles, celui qui exige que les expériences soient faites avec des détecteurs qui ne peuvent être connectés plus rapidement que la lumière pendant que l'on effectue des mesures sur des paires de particules intriquées. Alain AspectAlain Aspect avait déjà résolu ce problème en 1982 avec ses collègues. Un autre de ces points faibles est plus délicat, puisqu'il postule une certaine liberté dans le choix des mesures à faire par un observateur. Mais là aussi, on peut réaliser des expériences, comme celle d'Anton Zeilinger et ses collègues en 2010.
Le problème le plus facile à comprendre, mais qui s'est révélé peut-être le plus difficile à résoudre, est celui de l'efficacité de la détection des particules intriquées. En effet, notamment dans le cas des expériences avec les photonsphotons, quelques dizaines de pour cent de ceux crées lors de ces expériences sont détectés. On est donc contraint de postuler malgré tout que l'échantillonnageéchantillonnage est suffisamment important pour conduire à des conclusions solidessolides. Cela revient à postuler qu'un sondage réalisé avec un nombre restreint de personnes est finalement fiable pour prévoir l'issue une élection avec peu de chances de se tromper. Un opposant à l'interprétation orthodoxe de la mécanique quantique pouvait jusqu'à présent soutenir (bien que ce soit un peu tiré par les cheveux) que tous les tests avec des photons réalisés jusqu'ici n'étaient pas concluants en raison de ce problème d'échantillonnage.

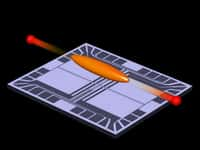
L'expérience qui a permis aux physiciens d'éliminer l’un des défauts des tests des inégalités de Bell. Elle a été menée par une équipe internationale de chercheurs américains et européens. © IQOQI Wien, Jacqueline Godany, 2012
Problème d'échantillonnage résolu
Une telle contestation est désormais impossible, comme l'a montré dernièrement un article publié dans Nature par Zeilinger et ses collègues. Les chercheurs ont utilisé des détecteurs de photons très efficaces. Il s'agit de systèmes supraconducteurssupraconducteurs refroidis à très basse température (100 mK), que l'on appelle des transition-edgeedge sensors (TES). Ils permettent de détecter 98 % des photons intriqués dans une expérience de test des inégalités de Bell. Le phénomène de l'intrication quantique est alors confirmé avec un écart aux prédictions des théories déterministes locales faisant intervenir 70 sigmas, comme on le dit dans le jargon des physiciensphysiciens. Rappelons qu'en physique, on accepte une découverte quand on obtient une mesure avec au moins 5 sigmas, comme ce fut le cas avec le boson de Higgs.
Nous sommes donc en présence d'un test extrêmement solide. Mais il faut garder à l'esprit, comme on le faisait remarquer précédemment, que les trois voies restantes pour contourner les tests portant sur les inégalités de Bell sont encore à fermer simultanément au sein d'une seule expérience.