au sommaire
Le nombre d'or, souvent désigné par Phi, enchevêtre toutes les apparences avec rigueur et équilibre parfait qui surprennent la raison par leurs agencements.

La suite géométrique de Fibonacci peut également être « complète ». Et voici son explication, ludique bien sûr. Nous avons établi graphiquement avec une ficelle et un triangle sublime les premiers éléments de la suite géométrique de Fibonacci :
1 Φ Φ2 Φ3... que l'on peut prolonger facilement : 1 Φ Φ2 Φ3 Φ4 Φ5 Φ6 Φ7...
Êtes-vous d'accord ? Amusez-vous à chercher graphiquement son prolongement, dans l'autre sens, à gauche de 1 avec la figure 1.
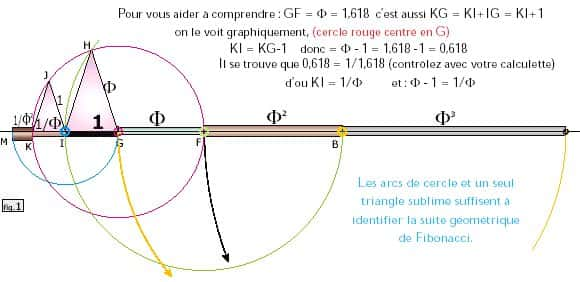
De même pour MK mais plus simplement, en généralisant :
- pour aller vers le plus grand, à droite, il faut multiplier par Φ (exemple Φ2 x Φ = Φ3 puis Φ3 x Φ = Φ4, etc.) ;
- pour aller vers le plus petit, à gauche, il faut diviser par Φ (exemple Φ/Φ = 1 1/Φ = 1/Φ et (1/Φ)Φ = 1/Φ2 ou encore (1/Φ2)/Φ = 1/Φ3 et ainsi de suite).
D'où la suite complète 1/Φ4 1/Φ3 1/Φ2 1 Φ Φ2 Φ3 Φ4 Φ5
Cette suite de Fibonacci est la plus simple qui puisse exister. C'est sans doute pour cette raison que nous la trouvons dans la nature, sur le fossilefossile ci-dessous par exemple, mais aussi sur des fleurs, des légumes, des arbresarbres et même sur nous !
Ce nombre d'or est surprenant
Avez-vous remarqué en regardant la figure 1 ci-dessus que :
- si l'on ajoute 1 à Φ on obtient son carré (1+Φ = Φ2) ;
- si l'on enlève 1 à Φ on obtient son inverse (Φ-1 = Φ/1).
C'est le seul nombre à réaliser cette prouesse ! Et si l'on considère les valeurs de Φ = 1,6180339... d'où Φ2 = 2,6180339... et 1Φ = 0,6180339... avec les mêmes chiffres (à l'infini) derrière la virgule, c'est encore plus remarquable.
Une suite géométrique de raison Phi dans un fossile vieux de 100 millions d'années
Regardez de près le fossile ci-dessous, une ammonite de 20 centimètres qui a 100 millions d'années. Son enroulement génère une suite de Fibonacci, les arcs de cercle le prouvent, de plus elle est géométrique de raison Φ tout comme la coquille d'escargot de la page 2. N'est-ce pas étonnant ?

Pour terminer, nous allons nous amuser à passer à la loupe le cœur de gerbera présenté en page 2.