au sommaire
Le fait que la conception d'un algorithme puisse demander la constructionconstruction d'un raisonnement fait que les mathématiques mésopotamiennes et égyptiennes posent rétrospectivement un problème : comment les Mésopotamiens, par exemple, ont-ils pu concevoir un algorithme pour la division sans avoir recours au raisonnement ? On doit supposer que les Mésopotamiens et les Égyptiens connaissaient une forme implicite de raisonnement. Le fait que, contrairement aux Grecs, ils n'aient pas rendu cette activité explicite, par exemple en écrivant leurs raisonnements sur des tablettes, et qu'ils n'aient sans doute pas eu conscience de l'importance du raisonnement dans la résolutionrésolution des problèmes mathématiques abstraits n'empêche pas qu'ils ont pu construire des raisonnements, comme Monsieur Jourdain faisait de la prose.

L'eau est selon Thalès le principe explicatif de toute chose. © Sven Hoppe, wikimedia commons, CC 3.0
Si on remarque souvent la nécessité de construire des raisonnements mathématiques pour concevoir des algorithmes, ce qui amène à supposer que les Mésopotamiens construisaient des raisonnements même s'ils ne les explicitaient pas, on remarque plus rarement que cette nécessité de construire des raisonnements pour concevoir des algorithmes éclaire le miracle grec : le passage du calcul au raisonnement. On peut, en effet, faire l'hypothèse que c'est en construisant des raisonnements pour concevoir de nouveaux algorithmes que les Grecs ont compris l'importance du raisonnement.
Par exemple, on attribue souvent le « premier » raisonnement géométrique à ThalèsThalès : pour mesurer la hauteur d'une pyramide trop haute pour une mesure directe, Thalès a eu l'idée de mesurer la longueur de l'ombre de la pyramide sur le sol et, indépendamment, la hauteur et la longueur de l'ombre d'un petit bâton, puis de faire une règle de trois.
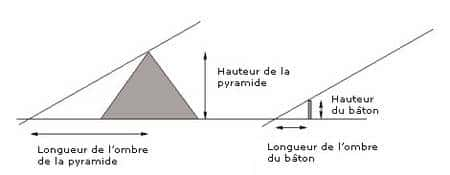
On peut faire l'hypothèse que le but de Thalès était de concevoir un nouvel algorithme pour calculer la longueur d'un segment et que, pour construire cet algorithme, il a eu besoin de démontrer que la pyramide avait avec son ombre le même rapport que le bâton avec la sienne. Théorème dont on a compris, par la suite, l'intérêt intrinsèque et que l'on appelle aujourd'hui le « théorème de Thalès ».