au sommaire
C'est ce type d'images qui a le plus contribué à l'impact artistique des fractales. Pourtant il s'agit au départ de travaux mathématiques très austères. En prolongeant d'anciens travaux de Fatou et Julia et en se servant des possibilités graphiques rudimentaires des ordinateursordinateurs de l'époque, Mandelbrot découvre les propriétés stupéfiantes d'un nouvel ensemble de nombres complexes.

Les nombres complexes
Pour comprendre de quoi il s'agit il faut expliquer (ou rappeler pour certains) ce que sont les nombres complexes. Ceci nécessite un détour par les nombres imaginaires. Le carré d'un nombre étant ce nombre multiplié par lui-même, un carré ne peut être que positif : en effet 4 est aussi bien le carré de 2 que celui de -2. Incidemment notons que 1 est le carré de 1 et de -1. Dans ces conditions un nombre négatif ne peut pas être un carré et la question « quelle est la racine carrée de -1 ? » n'a apparemment aucun sens. Ceci n'a pas arrêté les mathématiciensmathématiciens qui se sont demandé si l'on pouvait construire une arithmétique cohérente en supposant que -1 avait une racine imaginaire, désignée conventionnellement par i (l'autre racine étant -i.) La réponse est qu'en effet on peut construire une arithmétique englobant nos nombres usuels et des nombres imaginaires formés par le produit de i et d'un nombre réel quelconque (a.i).
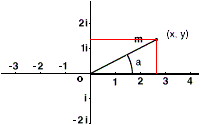
À partir de là, il est possible de définir les nombres complexes. Ceux-ci sont de la forme z = x + yi où x est la partie réelle et y la partie imaginaire. On peut représenter graphiquement ce nombre z dans un système de coordonnées planes puisque c'est un nombre à deux dimensions. Par convention, la partie réelle est affectée à l'axe des abscisses et la partie imaginaire à l'axe des ordonnées. Le nombre représenté ci-contre par le point m a pour coordonnées approximatives x=2,7 et y=1,3.
Le segment om a, d'après Pythagore, une longueur égale à la racine carrée de la somme des carrés de l'abscisse et de l'ordonnée :
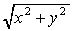
C'est le module du nombre complexe et ce nombre est un nombre réel. Il existe une arithmétique des nombres complexes qui utilise des règles un peu plus compliquées que notre arithmétique habituelle, mais qui permet d'effectuer sur les nombres complexes toutes les opérations classiques. Le plan défini par le système de coordonnées est appelé plan complexe.
Les ensembles de Julia et Fatou
Ceci étant expliqué, l'histoire de l'itération des polynômes complexes débute en 1918-1920, époque à laquelle deux mathématiciens, Julia et Fatou, publient les résultats de travaux conduits de façon totalement indépendante. Le plus simple des polynômes complexes étudiés ainsi est P(z)=z2+c ce qui conduit par itérations successives à la suite :
c est une constante complexe arbitraire et z est une variable également complexe. On calcule la valeur du polynôme pour une valeur de départ de z puis on donne à z la valeur ainsi trouvée et on recommence le calcul avec cette nouvelle valeur. Le résultat est à nouveau injecté dans z et on recommence, théoriquement un nombre infini de fois (z prenant à chaque itération la valeur trouvée dans le calcul précédent). Que constate-t-on alors ? Pour certaines valeurs de départ de z le résultat se maintient au fil des itérations successives dans un intervalle bien limité. Au contraire, pour d'autres valeurs, la fonction diverge et le point représentant le résultat s'échappe vers l'infini. En fait on démontre que le calcul divergera si au cours des itérations successives le module de z dépasse la valeur 2, ce qui permet d'arrêter le calcul dès que cette valeur est atteinte. Fatou et Julia s'étaient rendu compte du comportement très complexe des valeurs résultant de ce type de calcul, très long certes même si on s'arrête après un nombre raisonnable d'itérations, mais très simple dans son principe.
Malheureusement les ordinateurs n'existaient pas à l'époque et l'expression graphique des résultats était impossible sauf dans quelques cas simples. Si l'on se souvient que tout nombre complexe peut être représenté dans un plan avec les coordonnées x et y de sa partie réelle et de sa partie imaginaire, comment les valeurs de z pour lesquelles la valeur du polynôme ne diverge pas se répartissent-elles ?
Les points correspondants forment un ensemble bien défini dans le plan complexe, qu'on a pris l'habitude d'appeler un peu rapidement ensemble de Julia. Notons d'abord qu'il y a une infinité d'ensembles de Julia puisqu'on peut donner n'importe quelle valeur à la constante c. Pour certaines valeurs de c, les points sont rassemblés dans une surface qui forme une figure généralement assez compliquée mais connexeconnexe. Pour d'autres valeurs de c on obtient un ensemble « éclaté » formé de points séparés. Voici ce que cela donne lorsqu'on utilise l'écran pour représenter le plan complexe :

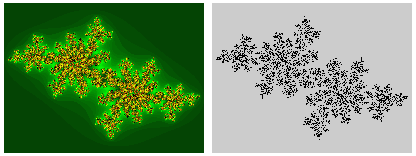
Dans cette représentation, les parties noires de l'image de droite représentent l'ensemble de Julia rempli. En effet l'ensemble de Julia est, à strictement parler, la limite de la zone noire de la première image, et la zone noire située à l'intérieur est l'ensemble de Fatou, mais on a pris l'habitude de parler d'ensemble de Julia sans faire cette distinction. Lorsque l'ensemble est non connexe, on peut démontrer qu'il a les propriétés d'une poussière de Cantor à deux dimensions (euclidiennes). Les auréoles colorées dans les images de gauches n'appartiennent pas à l'ensemble, mais, selon leur coloration, représentent les points qui échappent à l'ensemble au bout de 1, 2, 3, etc. itérations successives.

On voit qu'en choisissant judicieusement les couleurs, les zones qui entourent l'ensemble de Julia dessinent une structure très complexe et très belle.
L'ordinateur est un outil merveilleux pour exécuter la multitude de calculs bêtement répétitifs nécessaires à l'obtention de cette image. En effet il faut calculer z(n+1)=z(n)2+c pour chacun des points du plan complexe qui constituent l'image (soit 400x300=120.000 points pour l'image ci-dessus) avec un nombre d'itérations qui peut se mesurer en centaines pour chaque point.
Les ensembles de Julia sont fractals : on peut zoomer à l'infini dans l'image en trouvant toujours de nouveaux détails.
L'ensemble de Mandelbrot
Supposons maintenant que, dans le polynôme précédent, c ne soit plus une constante, mais une variable et représentons le résultat dans le plan complexe de c (et non dans le plan complexe de z comme dans le cas des ensembles de Julia). Pour chaque valeur de c, c'est-à-dire pour chaque pixelpixel de l'écran, itérons le polynôme en partant de la valeur z=0 et cherchons l'ensemble des points pour lesquels le polynôme ne diverge pas. Nous obtenons un nouvel ensemble qui a été découvert et étudié par Mandelbrot vers 1980. Son étude a été approfondie ultérieurement par Douady et Hubbard qui l'ont appelé ensemble de Mandelbrot (ou M). Mandelbrot insiste beaucoup dans son livre sur le fait qu'il a largement utilisé les possibilités graphiques des ordinateurs (pourtant très limitées à l'époque) pour étudier les propriétés de cet ensemble.
S'il y a une infinité d'ensembles de Julia il n'y a qu'un ensemble de Mandelbrot correspondant à la formule z(n+1)=z2(n)+c. Les points de l'ensemble de Mandelbrot (partie noire de l'image ci-dessous) sont l'ensemble des valeurs de c pour lesquelles l'ensemble de Julia correspondant est connexe. La frontière de l'ensemble de Mandelbrot est fractale, et sa dimension fractale est 2 (alors que sa dimension euclidienne est 1 puisque c'est une ligne). De la même manière que pour les ensembles de Julia, les zones colorées qui entourent la zone noire représentent les points qui échappent à l'ensemble après un certain nombre d'itérations.

L'ensemble de Mandelbrot est fractal et, en explorant l'image à des grossissements divers, on peut y trouver une infinité de détails spectaculaires. Comme pour toute figure fractale une caractéristique fondamentale est l'autosimilarité, c'est-à-dire qu'on va y retrouver à n'importe quel grossissement des structures semblables (ce qui ne veut pas dire strictement identiques) à celles qu'on observe à des grossissements moins élevés. En particulier une propriété très spectaculaire est la présence, cachée au milieu de structures variées, de mini-ensembles de Mandelbrot.
La figure suivante montre (en monochrome pour ne pas disperser l'attention, sauf pour la dernière image) une série de zooms successifs dans cet ensemble. Dans chaque image le cadre blanc montre la zone qui est agrandie dans l'image suivante.
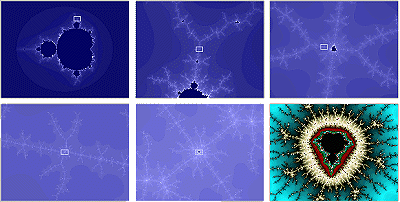
Et voici maintenant la même image agrandie :

L'ordinateur a permis de découvrir la beauté insoupçonnée de l'ensemble de Mandelbrot et des ensembles de Julia, objets mathématiques à première vue très abstraits. Ils sont à l'origine d'une branche nouvelle de l'art, appelée art fractal. De nombreux sites Web sont consacrés à ces images car InternetInternet est un moyen de diffusion particulièrement adapté pour les images informatiques.