au sommaire
Les observations, notamment celles menées dans le cadre du Sloan DigitalDigital Sky Survey (SDSS), montrent que l'univers n'est pas tout à fait homogène. Le modèle ΛCDM ou celui du vide minimal peuvent-ils expliquer cela ? Le point avec Philippe BraxPhilippe Brax, chercheur théoricien (interview complète pages 3 à 9 de ce dossier).
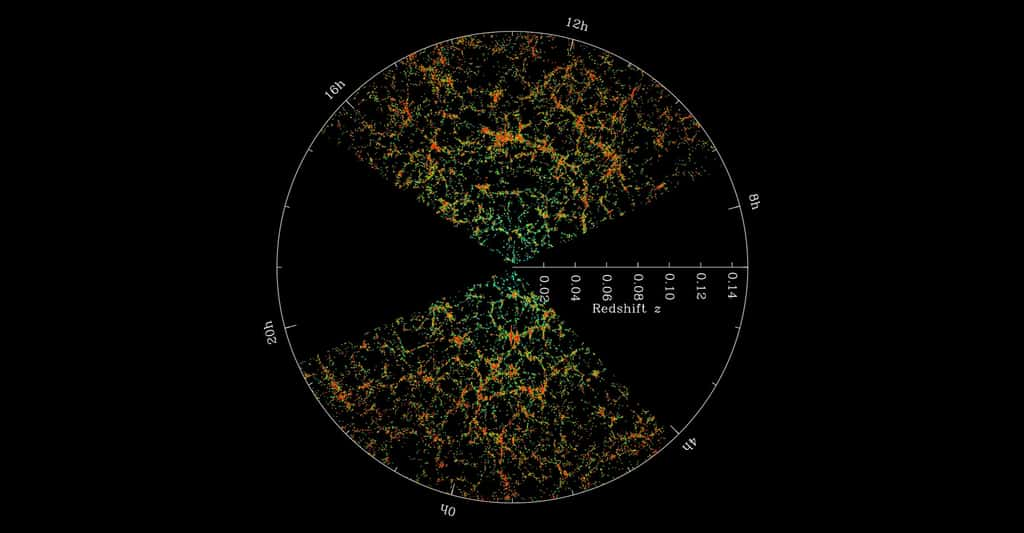
La campagne d'observations du Sloan Digital Sky Survey (SDSS). © M. Blanton and the Sloan Digital Sky Survey, DP

Une vue du télescope employé pour faire le Sloan Digital Sky Survey (SDSS). © David Kirkby
Peut-on justifier le principe cosmologique par des observations ?
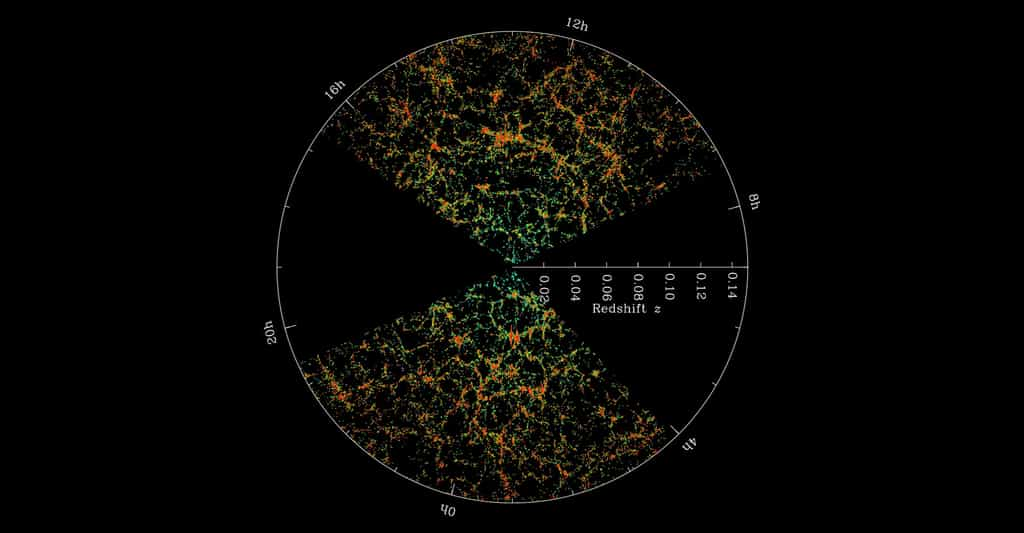
Philippe Brax : On a cherché à le faire en sondant l'univers de plus en plus loin et en mesurant les distributions de galaxies et de radiosources comme les quasars, de plus en plus précisément. Parmi les relevés de galaxies, on a en particulier eu le Sloan Digital Sky Survey (SDSS), celui de Las Campanas et enfin celui d'APM. Ils montrent qu'à des échelles supérieures à quelques centaines de millions d'années-lumière, l'univers n'est pas complètement homogène. Les amas de galaxies se rassemblent pour former des filaments et des mursmurs entourant des bulles vides.

Une illustration des observations soutenant le principe cosmologique pour l'univers observable. © Jean-Christophe Hamilton.
Toutefois, la distribution de ces bulles et filaments formant des superamassuperamas de galaxies montre une certaine homogénéité qui de prime abord semble suffisante pour une description effective du cosmoscosmos au-delà de ces échelles par un modèle FLRW.
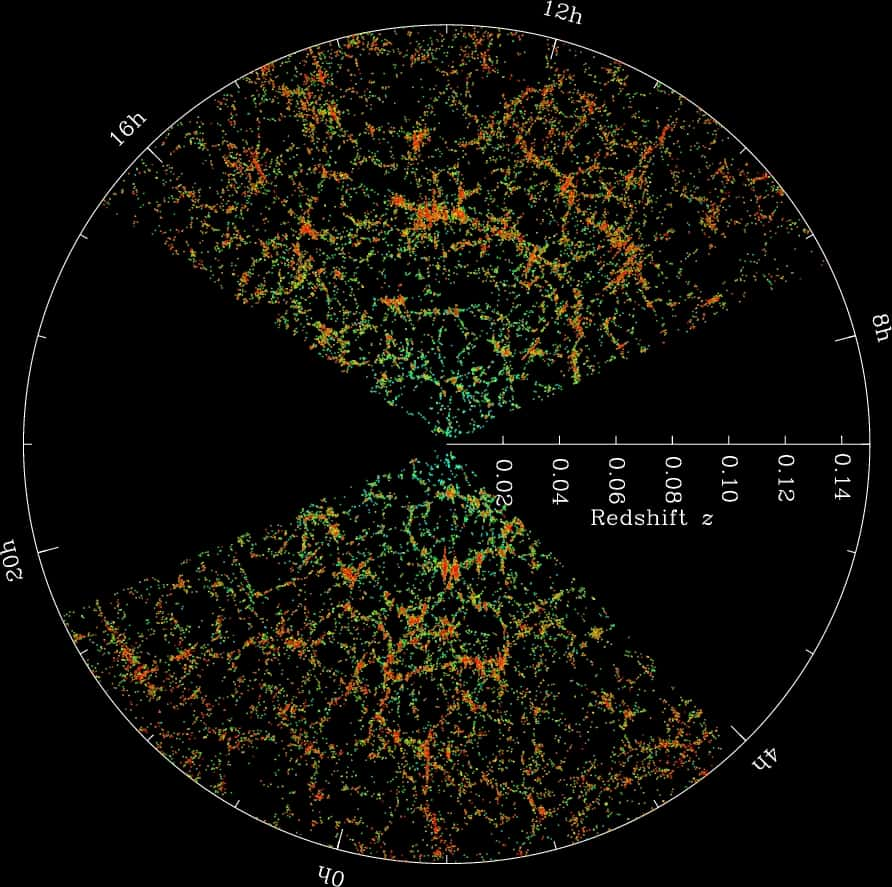
La campagne d'observations du Sloan Digital Sky Survey (SDSS) a permis de dresser une carte en 3D de la répartition des galaxies dont on voit une coupe ci-dessus. Chaque point représente une galaxie jusqu'à une distance de la Terre d'environ 2 milliards d'années-lumière. © SDSS.
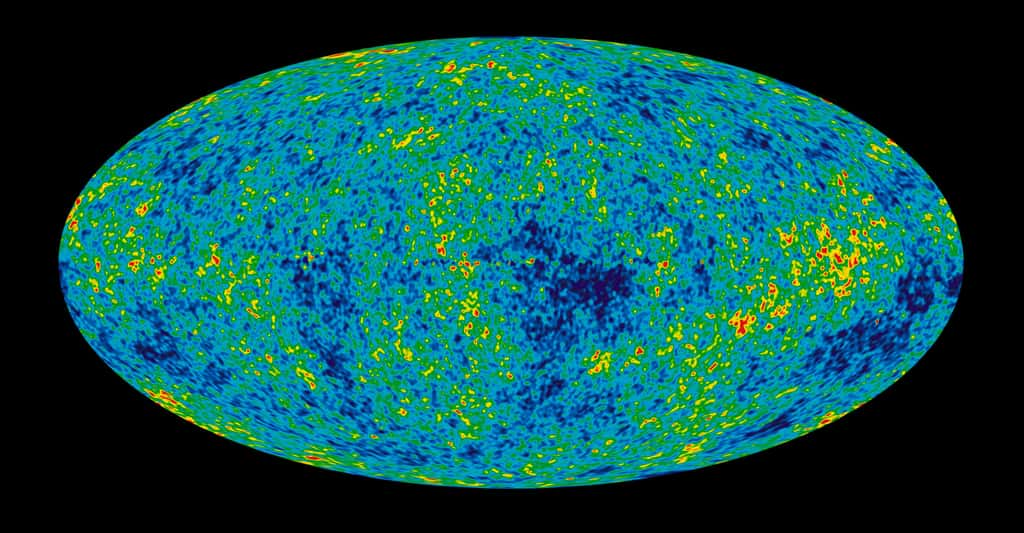
La véritable raison qui a fait que l'on considérait l'hypothèse d'homogénéité comme une très bonne approximation de l'univers observable depuis une vingtaine d'années, doit être recherchée au niveau du rayonnement fossile.
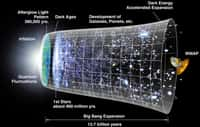
Les mesures de Cobe et WMap ont en effet établi que ce dernier était homogène et isotropeisotrope à 10-5 près. Les fluctuations de températures que l'on y mesure sont reliées aux fluctuations de densité dans l'univers primordial, 380.000 ans après la « naissance » du cosmos observable. Ces dernières étaient donc très faibles et cela donne beaucoup de poids au principe cosmologique. Ce n'est que plus tard, lorsque ces fluctuations de densité vont croître pour donner les structures en superamas actuelles, que l'univers observable va devenir moins homogène.
Cela ouvre donc la porte à une reconsidération de la solution des équations d’Einstein décrivant l’univers observable depuis quelques milliards d’années ?
Exactement. Si on prend l'analogieanalogie avec la surface de la Terre ou une surface plane, les modèles cosmologiques décrivent donc le cosmos comme s'il s'agissait de surfaces parfaites. On sait bien que celle de la Terre est bosselée et que l'image d'une sphère, ou plus précisément d'un ellipsoïde de rotation, parfaite n'est qu'une idéalisation de sa surface.
Il se trouve que, si l'on cherche une solution des équationséquations d'EinsteinEinstein plus réaliste décrivant l'univers observable, une moyenne sur les « bosses » de l'espace-tempsespace-temps dans le cas d'un univers relativiste inhomogène montre que la solution ce dernier s'écarte de celle d'un univers homogène, de la même façon qu'elle le ferait si l'on tenait compte de l'existence d'une constante cosmologiqueconstante cosmologique accélérant son expansion ! Celle-ci émerge donc directement sans que l'on ait besoin d'introduire de la nouvelle physiquephysique.
Il y a ainsi une solution des équations d'Einstein connue depuis longtemps et qui s'appelle la métrique de Tolman-Bondi, tout à fait appropriée pour décrire un tel univers inhomogène. Physiquement, on est ainsi conduit à postuler que nous serions à l'intérieur d'une zone de sous-densité dans l'univers, ce qui serait responsable du fait qu'elle soit en expansion accélérée. On parle de cette théorie en termes de scénario du vide minimal (Minimal Void ou MV en anglais). On peut montrer qu'il est possible d'être en accord de cette manière aussi bien avec les observations des supernovaesupernovae SNSN Ia qu'avec celles de WMap 3 et les calculs de la nucléosynthèsenucléosynthèse primordiale. Reste que pour cela, nous devrions être presque au centre de cette zone, ce qui est assez peu Copernicien.
Peut-on départager par des observations le modèle de concordance ΛCDM et celui du vide minimal ?
Le modèle ΛCDM est quand même celui qui reste le plus facile à mettre en accord avec les observations et qui colle le mieux avec celles-ci. Cependant, en procédant à des relevés de galaxies plus profonds dans l'univers, le modèle du vide minimal implique que l'on devrait mettre clairement en évidence que nous sommes dans une zone de sous-densité. Il serait possible aussi de voir que l'univers n'est pas localement en expansion avec la même vitessevitesse en fonction de la direction des observations. Une anisotropieanisotropie dans la valeur de la constante de Hubbleconstante de Hubble pourrait ainsi découler du modèle MV. Surtout, la courbe reliant luminositéluminosité et décalage spectral, qui a permis de découvrir l'expansion accélérée de l'universexpansion accélérée de l'univers grâce aux SN Ia, devrait posséder un pic caractéristique à la frontière séparant notre zone de sous-densité du reste de l'univers, comme le pensent Stephon Alexander, Tirthabir Biswas, Deepak Vaid et Alessio Notari.