au sommaire
La théorie des supercordes pourrait-elle résoudre le problème de la constante cosmologique ? Futura-Sciences a posé la question à Philippe BraxPhilippe Brax, chercheur théoricien (interview complète dans les pages 3 à 9 de ce dossier).

Simulation de la désintegration d'un boson de Higgs en 2 rayons de hadrons. © Lucas Taylor CERN, CC BY-SA 3.0
La théorie des supercordes, qui est justement la meilleure candidate au titre de théorie unifiée des interactions et surtout de théorie quantique de la gravitation, ne propose-t-elle pas de résoudre le problème de la constante cosmologique de cette façon ?
Philippe Brax : L'idée de base est effectivement un peu la même. En fait, la théorie des cordes introduit tout à la fois des champs supplémentaires et d'autres dimensions spatiales. Ces dernières nous seraient cachées parce que constituées de formes géométriques analogues à des bretzels et de très petites tailles. Dans ces dimensions spatiales supplémentaires compactifiées, formant ce qu'on appelle des espaces de Calabi-Yau, les champs supplémentaires s'y comportent un peu comme des champs magnétiques avec des énergies associées variant à la façon des niveaux d'énergies d'un atome.
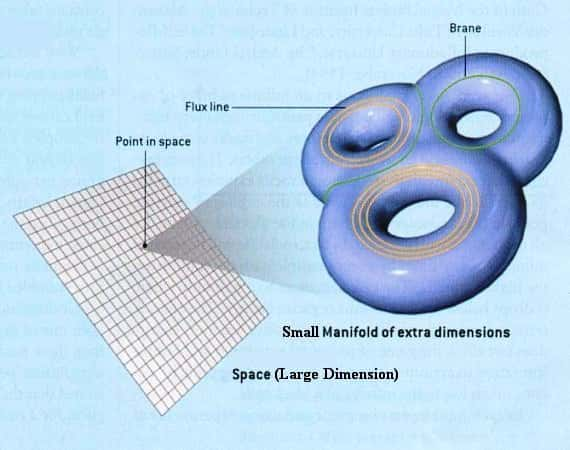
Dans un modèle simple de Kaluza-Klein et de théorie des cordes, représenté sur ce schéma, à tout point d'un univers de grande taille (Large Dimension) il existe des dimensions spatiales supplémentaires ayant la forme d'un espace de petite taille (Small Manifold) topologiquement compliqué et fermé sur lui-même. Dans cet espace, des lignes de champs analogues à celles d'un champ magnétique stabilisent ce dernier en l'empêchant de s'effondrer sur lui-même pour donner un trou noir, ou d'entrer en expansion comme les autres dimensions de cet univers. © Universe review
Ces niveaux d'énergies stabilisent les espaces de Calabi-Yau et les empêchent d'entrer en expansion ou de s'effondrer telle une étoileétoile donnant un trou noirtrou noir. Ce qui est intéressant, c'est que l'existence de ces espaces et de ces nouveaux champs (décrits par ce qu'on appelle des p-formes) est équivalente à l'apparition d'un très grand nombre de contributions à l'énergie du vide, similaires à celle d'un champ de Higgs.
Michael Green, avec en haut à gauche la formule de Veneziano qui a mis sur la piste de la théorie des cordes. La formule de Veneziano permet de reproduire une partie du comportement des mésons de la théorie des forces nucléaires fortes. Avec John Schwarz il a été à l'origine de la première révolution de la théorie des supercordes en 1984, dans laquelle plusieurs physiciens de premier plan ont basculé, comme le prix Nobel de physique 1979 Steven Weinberg et Edward Witten, qui a reçu la médaille Fields en 1990. © Université de Cambridge
Il existe alors un nombre immense d'états de vide possibles selon la valeur de ces champs qui se retrouvent sur une surface à plusieurs dimensions, et bien plus compliquée que celle en forme de sombrero du champs de Brout-Englert-Higgs. En fait, si on gardait une image à deux dimensions, c'est un peu comme si les différents états d'énergies possibles étaient représentés par la topographie d'un paysage, avec des vallées, des cuvettes et des collines.
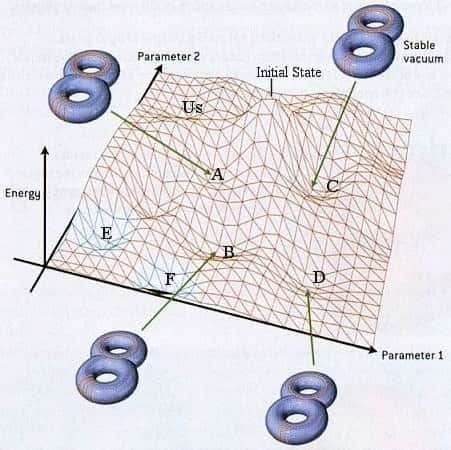
Le paysage cosmique d'un « univers jouet », avec deux dimensions spatiales compactes supplémentaires enroulées sous la forme d'un tore de genre 2. Ces tores sont stabilisés dans différents états de tailles et de formes par les modes d'enroulement des cordes/membranes et les flux « magnétiques » des champs introduits par la présence des membranes de la théorie des supercordes. À un couple de deux paramètres décrivant les tores, correspond un état d'énergie du vide possible sur la surface. © Universe review
Comme ces états d'énergies représentent en fait des valeurs possibles de la constante cosmologique, on en parle sous le nom de Paysage Cosmique, en anglais « Cosmological Landscape ». Généralement, le simple terme « Landscape » est utilisé.
Initialement, on se retrouve devant le même problème de réglage fin des lois physiquesphysiques pour qu'existe une faible valeur de la constante cosmologique, mais celui-ci apparaît sous un nouveau jour. Pour bien le comprendre, il faut mentionner la contribution à la fin des années quatre-vingt du prix Nobel de physique Steven WeinbergSteven Weinberg.

Le prix Nobel de physique Steven Weinberg. © Goethe Universität Frankfurt am Main
Weinberg a fait remarquer, calculs à l'appui, que si une constante cosmologique accélérant l'expansion de l'universunivers existait, elle ne pouvait pas être trop grande sans empêcher la formation d'étoiles et de galaxiesgalaxies. Elle doit même être vraiment très faible. Dès lors, il n'y aurait d'une certaine façon pas vraiment de raisons de s'étonner de sa faiblesse, car dans le cas contraire nous ne serions pas là pour observer la présence de cette constante. Ce genre de raisonnement, montrant un lien entre la présence de l'Homme dans l'univers et la structure de ces lois, s'appelle un argument anthropique.
Maintenant, il y aurait au moins 10500 états du vide possibles selon la théorie des cordesthéorie des cordes, ce qui fait qu'il doit exister un nombre important d'univers possibles dans lesquels les différentes contributions des énergies du vide peuvent presque s'annuler. Si l'on imagine un multivers constitué d'univers poches avec toutes les énergies du vide possible, certains auront une faible valeur et donc une faible constante cosmologique. Il n'y aurait que dans ces univers-là que la vie pourrait se développer.
Il n'y aurait donc pas besoin d'exiger un réglage fin des lois de la physique, ni de raison de s'en étonner, pas plus qu'il n'y a de raison de s'étonner que la Terre soit située à bonne distance d'une étoile brillant suffisamment longtemps pour que la vie se développe dans une galaxie constituée de centaines de milliards d'étoiles.