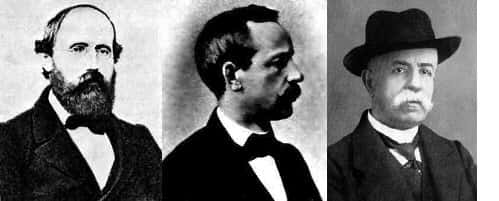au sommaire
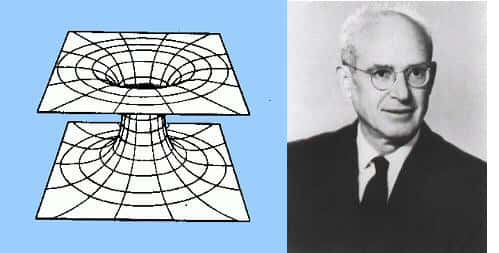
Le pont d'Einstein-Rosen et les trous de ver de Wheeler-Misner
Lorsqu'on aborde le sujet de l'espace-temps, deux notions essentielles sont à considérer : le pont d'EinsteinEinstein-Rosen et les trous de ver de Wheeler-Misner.

Pont d'Einstein-Rosen - Nathan Rosen. © DR
Le pont d'Einstein-Rosen
Dans sa quête de l'unification des forces et de la matière avec la géométrie de l'espace-temps, Einstein proposa, avec son collaborateur Nathan Rosen, une légère extension de la solution de Schwarzschild à la suite d'une analyse plus poussée de celle-ci. Le caractère atomique de la matière pouvait alors être interprété comme l'existence d'un pont entre deux feuillets d'espace-temps. Cela réalisait le vieux rêve d'Einstein d'une théorie non dualiste de la matière où les particules seraient des solutions des équations du champ de gravitation convenablement comprises et généralisées, pas des hypothèses indépendantes et surajoutées à ces dernières.
On pourra voir ci-dessous l'introduction de ce célèbre article.

L'article d'Einstein et Nathan Rosen.
C'est vraiment de là que date le début des spéculations sérieuses sur des raccourcis possibles dans l'espace-temps ou des passages entre des univers parallèles.
Regardons à nouveau la solution de Schwarzschild liée au pont d'Einstein-Rosen. Lorsque r devient inférieur à 2GM, on voit que les signes devant les deux premiers termes s'inversent, r prend la place du temps qui devient espace !
La géométrie est en réalité dynamique pour un observateur interne se dirigeant vers r=0.
La taille de la gorge du pont se met à diminuer et le voyageur aventureux se fait écraser complètement en ce point r=0 où se trouve la singularité.
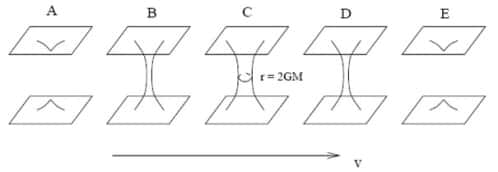
La coordonnée v est reliée à l'écoulement du temps dans la géométrie de Schwarzschild mais décrite selon le système de coordonnées de Kruskal. © DR
Réduite à deux dimensions, la géométrie de l'espace temps se représente par le diagramme de plongementdiagramme de plongement ci-dessus. Le passage subit un étranglement au fur et à mesure que le temps passe pour l'observateur précédent.
On ne peut donc pas voyager par un trou noirtrou noir car on se fait écraser par la singularité avant de pouvoir traverser le pont découvert par Einstein et Rosen.
Comme on l'a dit plus haut, la solution de Schwarzschild semblait pathologiquepathologique pour les contemporains d'Einstein car lorsque r était égal à 2GM les coefficients de la métrique s'annulaient ou devenaient infinis. Longtemps on a cru que cela signifiait qu'on ne pouvait pas considérer une étoileétoile dont la massemasse était située sous ce rayon limite noté Rs. Eddington et Lemaître avaient bien noté qu'il s'agissait juste d'un mauvais choix de coordonnées et absolument pas d'un problème avec la structure géométrique de la solution mais leurs remarques étaient passées inaperçues.
On peut le voir en construisant des quantités que l'on appelle des invariants à partir du tenseur de courbure.
Comme son nom l'indique un invariantinvariant peut être calculé dans un système de coordonnées mais sa valeur en est indépendante. Dans le cas de Schwarzschild si l'on considère l'invariant ci-dessous :
obtenu à partir du fameux tenseurtenseur de courbure de Riemann.
On voit que les problèmes n'arrivent que quand r est nul, ce qui est justement, on l'a dit, l'existence d'une singularité au centre de la solution. Ce n'est que plus tard, à partir de systèmes de coordonnées introduits par Finkelstein et Kruskal, à la fin des années 1950, qu'on a pu décrire correctement ce qui se passait, à savoir rien, lors du franchissement de la surface déterminée par Rs.
Cette surface est pourtant loin d'être anodine et l'on finira par lui donner le nom d'horizon des événementshorizon des événements car rien de ce qui pénètre à l'intérieur de la région déterminée par celle-ci ne peut plus en sortir ni influer sur l'extérieur en envoyant un signal. L'existence d'un horizon pour un objet compact est en fait la définition même de ce qui sera baptisé plus tard un trou noir.
Les trous de ver de Wheeler-Misner
Vers la même époque, John Wheeler, coauteur de la première théorie de la fissionfission avec Niels BohrNiels Bohr et directeur de thèse de Feynman, utilisa tout de même le concept de pont d'Einstein-Rosen pour décrire comme eux les particules chargées et leurs masses. C'est d'ailleurs à lui qu'on doit la dénomination trou de ver (wormhole) et structure en écumeécume (foam like structure), sans oublier bien sûr le mot trou noir (black hole) !

Collègue d'Einstein à Princeton, il n'est pas étonnant qu'il se soit alors laissé influencer par son idée de réduire toute la physiquephysique des forces et des particules à des structures géométriques.
À cause de son travail sur l'hydrodynamique des explosions nucléaires et en raison du parallèle entre la structure non linéaire des équations de la mécanique des fluides et de la relativité généralerelativité générale, il prit l'habitude de comparer la dynamique de la géométrie de l'espace-temps à celle des fluides.
Ainsi la formation de trous de ver ou même de trous noirs dans l'espace-temps est l'analogue de la formation d'écume, de bulles lorsque se brisent les vaguesvagues.
On lui doit en ce sens des articles séminaux dans lesquels il introduisit le concept de géométrodynamique, aussi bien en référence à l'hydrodynamique qu'à l'électrodynamique (classique et quantique).

John Archibald Wheeler. De même que la mer semble lisse à grande altitude, même si une tempête l'agite, l'espace-temps à l'échelle microscopique est secoué de violentes fluctuations. © DR
Peut-être vous êtes vous demandé pourquoi dans la série télévisée Stargate SG1 l'ouverture de la porteporte des étoiles s'accompagne toujours de quelque chose ressemblant à une surface d'eau légèrement agitée, vous avez maintenant la réponse !

La matière au centre de la porte des étoiles n'est désormais plus un mystère pour vous ! © DR
On peut montrer que les particules ainsi conçues sont aussi porteuses de masse. C'est ce que Wheeler a exprimé en parlant de « charge without charge, mass without mass ». Toute séduisante que soit cette image elle n'a jamais permis de retrouver les valeurs exactes de la masse des électronsélectrons (par exemple) ni de leur charge car on trouve plutôt des particules liées à l'échelle de PlanckPlanck et donc sans connexions évidentes avec les observations.
En généralisant cela avec l'image « foam like » de l'espace-temps à petite échelle de Wheeler, on obtient l'image topologiquement tourmentée suivante.
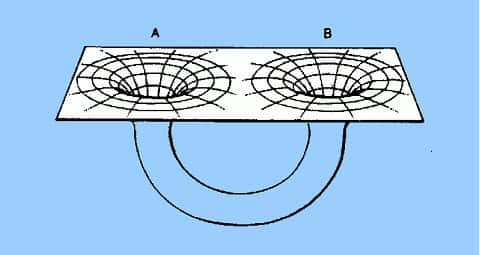
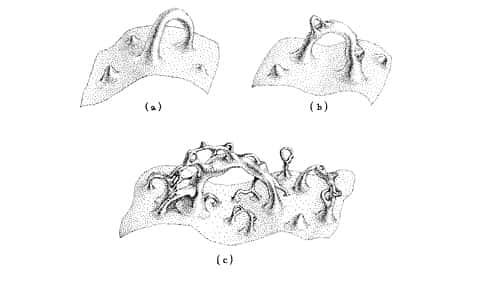
Structure en écume de l'espace-temps. © Kip Thorne
Regardons d'un peu plus près cette histoire de structure en écume de l'espace-temps.
On peut considérer la déviation
de la métrique de l'espace-temps par rapport à la métrique plate
dans un volumevolume très petit de celui-ci. La mécanique quantiquemécanique quantique nous apprend que pour chaque composante possible de longueur d'ondelongueur d'onde L d'un champ dans un volume d'espace-temps L4 il existe un demi-quantum d'énergieénergie associé aux fluctuations d'énergie du vide et fonction de cette longueur d'onde. On peut en effet, en espace-temps plat au moins, décomposer la majeure partie des champs physiques en superposition d'oscillations et de vibrationsvibrations élémentaires de longueurs d'onde données. Chaque oscillation est définie comme un mode, pensez à une corde vibrante.
Le champ gravitationnel ne doit pas faire exception à la règle, d'autant plus que l'on peut écrire une équation linéaire décrivant les fluctuations de ce champ par rapport à un espace-temps plat très similaire à celles décrivant les autres champs dans la même situation.
La densité d'énergie pour un mode de longueur L est
Ce qui pour un volume d'espace L3 donne une fluctuation d'énergie
Ainsi la fluctuation de métrique associée à ce mode est
Si l'on essaie de mesurer une longueur on aura ainsi une erreur inévitable
Une limite à la notion classique de longueur pour l'espace-temps émerge alors car c'est uniquement pour L telle que qu'une image lisse et stable de la géométrie de l'espace-temps peut être maintenue. On voit apparaître une longueur caractéristique (si l'on pose G=c=1 avec des unités convenables)
Cette valeur est appelée la longueur de Plancklongueur de Planck-Wheeler.
À cette échelle, l'espace-temps devient « turbulent » et doit être décrit par une théorie quantique de la gravitation. C'est précisément ce qui doit se produire aussi au voisinage des singularités classiques que l'on trouve à l'intérieur des trous noirs et à l'origine de l'univers.
Une conséquence de cette « turbulenceturbulence » est l'apparition de l'analogue de la cavitationcavitation (formation de bulles) en hydrodynamique, naturellement il s'agit de l'apparition/disparition de minitrous de ver, lesquels peuvent alors s'interpréter comme des paires de particules/antiparticulesantiparticules apparaissant et disparaissant sans cesse.