au sommaire
Certains physiciensphysiciens, tout en admettant la réalité de l'accélération récente de l'expansion de l'univers, pensent qu'avant d'invoquer de la nouvelle physique, il faudrait peut-être chercher du côté des hypothèses sur lesquelles les modèles cosmologiques sont construits à partir de la relativité générale. Nous avons interrogé le chercheur théoricien Philippe BraxPhilippe Brax à ce sujet (interview complète pages 3 à 9 de ce dossier).
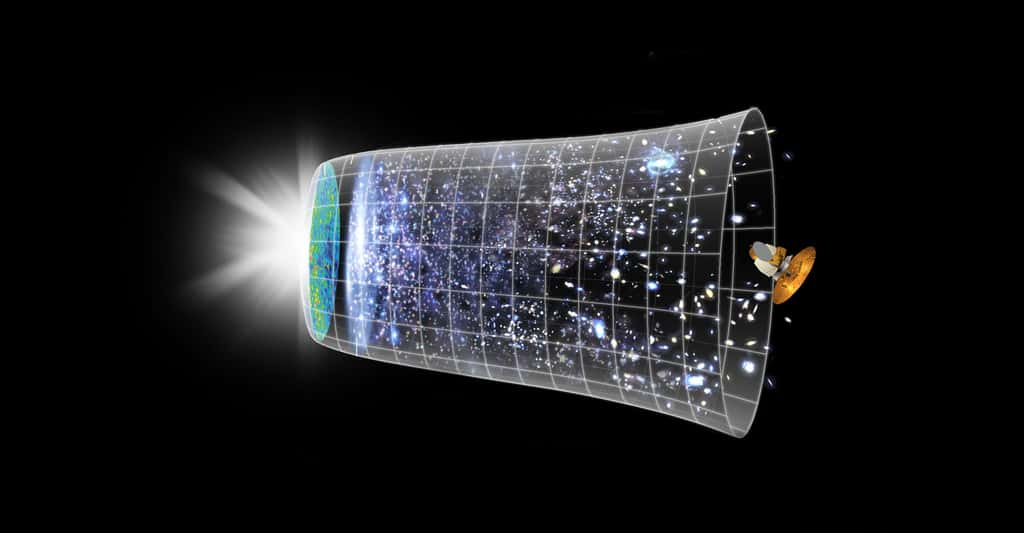
L'accélération de l'expansion de l'univers impliquerait l'existence d'une énergie noire. © Nasa, DP
Certains physiciens proposent de remettre en cause l’hypothèse d’homogénéité de l'univers. Que faut-il en penser ?
Philippe Brax : C'est une direction de recherche qui est de plus en plus explorée depuis quelques années. Pour bien comprendre de quoi il s'agit il faut en revenir aux hypothèses de bases de la cosmologie moderne. Il y a d'abord bien sûr celle que l'univers observable est bien décrit par la théorie de la relativité générale. Cela pose déjà de multiples problèmes lorsque l'on veut appliquer cette théorie à l'univers dans son ensemble.
Les équations d'EinsteinEinstein sont non linéaires et personne n'a été capable de trouver une solution générale à ces équations. C'est un problème très difficile et probablement au-delà de la portée de l'esprit humain. On ne sait généralement résoudre des équations non linéaires que sous certaines hypothèses simplificatrices, ou alors avec l'aide d'ordinateursordinateurs. L'exemple type à cet égard est celui de la mécanique des fluides.

À gauche, Edwin Hubble, le découvreur de l'expansion de l'univers et, à droite, Albert Einstein avec l'abbé Lemaître. Il est juste de dire que Georges Lemaître a complètement dominé la cosmologie relativiste à ses débuts, anticipant bien des aspects du modèle standard actuel avec sa théorie de l'atome primitif, ses réflexions sur la constante cosmologique, la naissance des galaxies et la cosmologie quantique. © 2015, American Institute of Physics
Plus encore que la théorie de la relativité restreinte, la théorie de la relativité générale bouleverse nos intuitions sur le temps et l'espace en faisant dépendre les caractéristiques de ces derniers des distributions de matièrematière et d'énergieénergie. Dans quel sens peut-on en effet parler d'un temps cosmique, d'une histoire générale de l'univers observable, si l'écoulement du temps n'est pas le même en fonction de ces distributions dans l'espace ?
Pour résoudre simultanément ces problèmes, les pionniers de la cosmologie relativiste, parmi lesquels on trouve Einstein et Herman Weyl, se sont appuyés sur une hypothèse connue sous le nom de principe cosmologique : « L'univers est homogène et isotropeisotrope à grande échelle ».
Implicitement, il affirme que notre galaxiegalaxie n'occupe pas de place particulière dans l'espace et qu'à des échelles supérieures à celles des amas de galaxiesamas de galaxies, l'univers observable apparaît identique à tous les observateurs. Depuis l'époque de CopernicCopernic, cela semble une affirmation raisonnable.
Précisons un peu ce que l'on entend par homogène et isotrope.

En haut de cette image, on voit les équations d'Einstein complétées par un terme Λ. Il s'agit de la fameuse constante cosmologique. Ces équations, sous certaines hypothèses simplificatrices, admettent une solution cosmologique dite de Friedmann-Lemaître-Robertson-Walker (FLRW). La géométrie de cette solution est alors de 3 types possibles en ce qui concerne la courbure (paramètre k) et il suffit d'une fonction a(t) pour décrire l'expansion de l'espace au cours du temps. © Jean-Christophe Hamilton
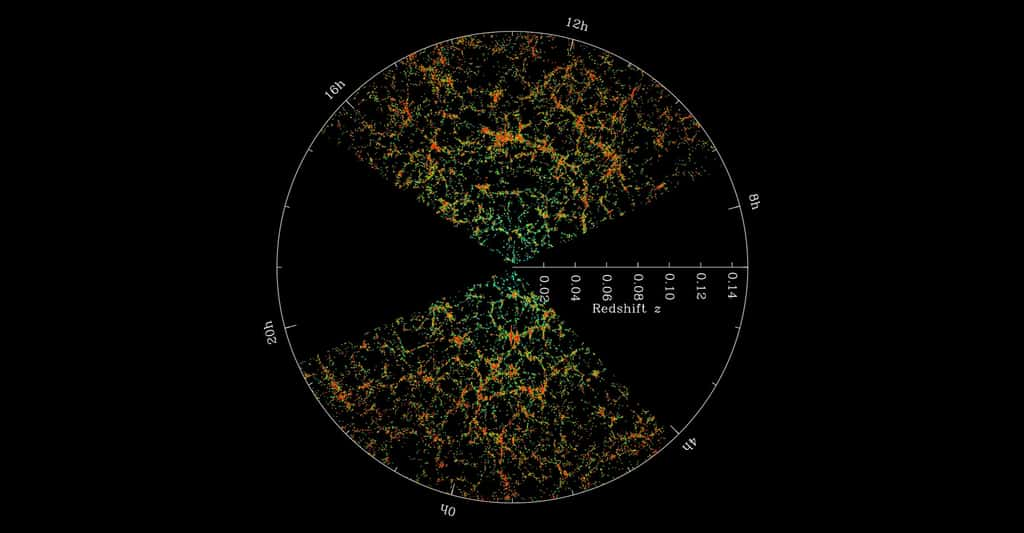
L'homogénéité signifie que, de même qu'à notre échelle, l'eau apparaît comme un fluide de densité uniforme, malgré le fait qu'elle soit en fait formée de moléculesmolécules, le « fluide » de galaxies possède lui-aussi une densité constante lorsqu'on le regarde à une très grande échelle, supérieure à des centaines de millions d'années-lumièreannées-lumière. L'isotropieisotropie indique quant à elle que l'univers apparaît comme identique à lui-même dans toutes les directions avec une excellente approximation. Dit autrement, on ne voit pas des caractéristiques différentes pour les galaxies selon que l'on regarde dans telle ou telle direction sur la sphère céleste.

En résolvant les équations d'Einstein pour un modèle cosmologique dit de FRLW, apparaissent deux équations différentielles simples, dites de Friedmann, décrivant la vitesse et l'accélération ä(t) de l'expansion à partir du facteur d'échelle a(t), en fonction de la constante cosmologique Λ, de la pression p et de la densité Ρ de matière et de rayonnement. © Jean-Christophe Hamilton.
Il se trouve que ces hypothèses simplifient énormément la résolutionrésolution des équations d'Einstein. De plus, l'hypothèse d'homogénéité implique automatiquement l'existence d'un temps cosmique partagé par toutes les galaxies et qui permet de parler d'une histoire de l'univers observable. Les simplifications sont même si spectaculaires qu'il ne reste plus que trois types de géométrie de l'espace-tempsespace-temps, celles décrites par les modèles de Robertson-Walker (RW) mais déjà explorées par Friedmann et Lemaître. La géométrie du cosmoscosmos peut alors être vue comme l'analogue de celle d'une sphère, d'un plan infini ou encore d'une selle de cheval.