au sommaire
L'article dont Kronecker a retardé la publication (voir page précédente) contient un résultat de Cantor tout à fait étonnant qui, bien que ne constituant pas un paradoxe, fut à n'en pas douter considéré sur le moment comme créant une situation logiquement peu satisfaisante.

Des chiffres à l'infini. © Tostphoto, Fotolia
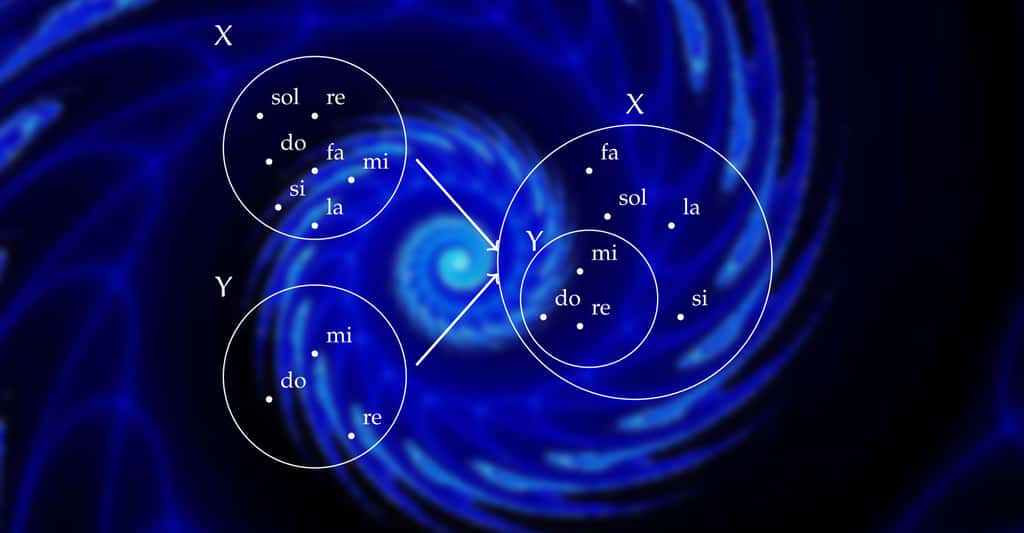
Cantor, toujours occupé à classer les infinis, a en effet découvert avec stupeur que l'ensemble des points d'une surface (un carré, par exemple) possède la même taille que l'ensemble des points d'un segment de droite. Du point de vue de leur taille d'ensemble infini, une droite et un plan (ou même un espace de dimension n) sont identiques. Il écrira à Dedekind à ce propos : « Je le vois, mais je ne le crois pas. »
Cantor adopte l'attitude téméraire qui consiste à accepter cette nouvelle vérité sans la décréter paradoxale, malgré la gêne qu'elle engendre. Comme aucune contradiction véritable ne découle des raisonnements et des calculs que Cantor élabore avec soin, il faut avoir l'audace d'accepter ce que nos facultés de raisonnement produisent et, aussi déconcertante que soit cette nouvelle réalité de l'infini actuel, il faut en poursuivre l'exploration. À vrai dire, au tournant du XXe siècle, certaines contradictions (ce qu'on appellera les antinomies) sembleront rendre la constructionconstruction cantorienne intenable. Toutefois, en quelques années, ces difficultés seront circonscrites (plusieurs méthodes seront même proposées), et ce qui apparut à certains comme la faillite de la théorie mathématique de l’infini actuel sera en définitive l'occasion pour cette théorie de se forger une armure qu'aujourd'hui rien n'est venu sérieusement érafler.

Au cours de ses travaux, Georg Cantor a distingué deux types de nombres infinis, les cardinaux et les ordinaux, pour son arithmétique de l'infini. © DP
Revenons à Cantor qui, en théoricien consciencieux, développe une arithmétique de l'infini, c'est-à-dire une extension, aux nombres qui lui servent à mesurer l'infini, des règles de calcul qu'on applique aux nombres entiers, servant à mesurer le fini. À cette occasion, il est contraint de distinguer deux types de nombres infinis, les cardinaux et les ordinaux. Les cardinaux sont les tailles des ensembles quand on les considère de manière brute, sans tenir compte d'un possible ordre entre leurs éléments. Cantor introduit en 1893 la notation pour le cardinal de l'ensemble des nombres entiers,
pour le cardinal du continu (l'ensemble des nombres réels), qui est le même que celui de P(ℕ), l'ensemble des parties de N. Il utilise
pour le cardinal de P(P(ℕ)), etc.