Inégalités de Heisenberg : qu'est-ce que c'est ?

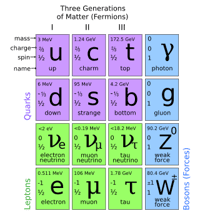
Mal nommé, le principe d'incertitude de Heisenberg est plus correctement désigné aujourd'hui sous le terme des inégalités de Heisenberg. Ces inégalités, énoncées en 1927 par le physicienphysicien allemand Karl Werner HeisenbergWerner Heisenberg, nous indiquent les limites sur la pertinence de l'emploi des concepts d'ondes et de particules classiques pour décrire les phénomènes à l'échelle atomique, comme ceux portant sur les électrons et la lumière.

Encore abusivement, on les nomme relations d'incertitudes ou d'indéterminations.

Les trois inégalités de Heisenberg :

i variant de 1 à 3 pour exprimer x,y,z

= racine carrée de l'écart quadratique moyen sur la mesure de la position = racine carrée de l'écart quadratique moyen sur la quantité de mouvement = constante de Planck divisée par

En aucun cas, elles n'indiquent une imprécision ou une limite à la connaissance simultanée de la position et de la quantité de mouvement d'une particule au sens classique. Elles ne reflètent pas une limite à la connaissance mais une limite à l'applicationapplication des concepts classiques pour décrire les phénomènes mécaniques à l'échelle de l'atomeatome.

Si l'on persiste à décrire la matièrematière et la lumière en termes de particules et d'ondes, on ne peut le faire qu'en limitant ces concepts l'un par l'autre et en donnant des probabilités d'observations de telle ou telle valeur classique d'un objet classique. Le vecteur d'état d'une particule dans l'espace prend alors la forme d'une fonction d'onde donnant la probabilité d'observation avec un appareil classique de l'aspect particule d'un quanta d'énergieénergie en un point de l'espace.

Il s'introduit alors un calcul avec des valeurs moyennes et des écarts quadratiques moyens mais il ne s'agit absolument pas de méthodes probabilistes utilisées pour décrire un système classique, ou plus exactement une population de systèmes, dont certaines informations déterminant l'état nous manqueraient, comme c'est le cas en théorie cinétique des gazgaz.

Il s'agit en fait d'une reformulation générale du caractère et de l'évolution d'une grandeur physiquephysique observable dans l'UniversUnivers.

Si l'on considère une fonction d'état pour des grandeurs A et B, qui peuvent ne rien avoir à faire avec une image d'onde ou de particule, alors si ces grandeurs sont conjuguées au sens de la théorie de Hamilton dans un système possédant une fonction d'énergie H, elles vérifieront une inégalité de Heisenberg.

Ainsi on pourra avoir les champs électriquechamps électrique E et magnétique B, l'énergie E et le temps t, un moment cinétiquemoment cinétique J et un angle etc...