Selon certains calculs en théorie des supercordes, les trous noirs n'existeraient pas mais à la place se formeraient des objets ayant des propriétés similaires appelés des « fuzzballs ». Ces boules diffuses de supercordes auraient des signatures particulières sous forme d'ondes gravitationnelles lors de collisions d'astres que nous pensons, à tort, être de vrais trous noirs.
au sommaire
Depuis la détection des ondes gravitationnellesondes gravitationnelles en 2015 et à un moindre degré grâce aux images de la collaboration Event Horizon Telescope, on pourrait croire que l'existence des trous noirs est un fait avéré. On peut le penser mais on ne peut pas encore l'affirmer et une récente publication dans le célèbre et réputé journal Physical Review D apporte de l'eau au moulin de ceux qui pensent que non seulement les trous noirs n'existent pas mais qu'il sera bientôt possible de le démontrer grâce à l'astronomie gravitationnelle et aux progrès des détecteurs tels LigoLigo et VirgoVirgo.
L'article à ce sujet provient d'une équipe de physiciensphysiciens basée à l'université de Rome « La Sapienza », la principale université italienne, et il est en accès libre sur arXiv. Pour comprendre de quoi il en retourne, remontons au début des années 1980, alors que ce qui a été baptisé l'âge d'or de la théorie des trous noirs prend fin, et que les théories de la supergravité et dans une moindre mesure des supercordes sont en plein essor.
Suite à ses impressionnants travaux en astrophysique, Subrahmanyan ChandrasekharSubrahmanyan Chandrasekhar se voit remettre le prix Nobel de physique en 1983. Comme d'habitude pour la remise de ce prix, le lauréat donne une conférence. À la fin de celle du grand astrophysicienastrophysicien indien, on trouve de fascinantes remarques concernant la théorie mathématique des trous noirs, qui sont à peu près les suivantes :
Un clip vidéo de Subramanyan Chandrasekhar, recevant sa médaille et son diplôme lors de la cérémonie de remise du prix Nobel au Concert Hall de Stockholm, en Suède, le 10 décembre 1983. Pour obtenir une traduction en français assez fidèle, cliquez sur le rectangle blanc en bas à droite. Les sous-titres en anglais devraient alors apparaître. Cliquez ensuite sur l'écrou à droite du rectangle, puis sur « Sous-titres » et enfin sur « Traduire automatiquement ». Choisissez « Français ». © Nobel Prize
« Je ne sais pas si toute la portée de ce que j'ai dit est claire. Laissez-moi vous expliquer. Les trous noirs sont des objets macroscopiques avec des masses variant de quelques masses solaires à des milliards de masses solaires. Lorsqu'ils peuvent être considérés comme stationnaires et isolés, ils sont tous, chacun d'entre eux, décrits exactement par la solution de Kerr. C'est le seul cas connu où nous avons une description exacte d'un objet macroscopique.
Les objets macroscopiques tout autour de nous sont régis par une variété de forces, décrites par diverses approximations de plusieurs théories physiques.
En revanche, les seuls éléments de constructionconstruction de trous noirs sont nos concepts de base de l'espace et du temps. Ils sont ainsi, presque par définition, les objets macroscopiques les plus parfaits de l'Univers. Et puisque la théorie de la relativité générale nous fournit une famille de solutions dépendant uniquement de deux paramètres pour leur description, ils sont aussi les objets les plus simples de l'Univers. »
Cette simple remarque est à la racine du fameux paradoxe de l'information découlant de la découverte par Stephen Hawking du fameux rayonnement quantique des trous noirs.
En effet, les remarques de Chandrasekhar concernent la théorie des trous noirs déduite rigoureusement de la théorie de la relativité générale d'EinsteinEinstein. Comme Hawking et un autre prix Nobel de physique, Roger Penrose vont abondamment le montrer avec leurs collègues, dans le cadre de cette théorie on se doit de considérer que ce qui définit un trou noir c'est uniquement l'existence d'un horizon des événementshorizon des événements et absolument pas l'existence d'une singularité de l'espace-tempsespace-temps. Cet horizon des événements est une surface fermée constituant une frontière entourant une région dans laquelle on ne peut qu'entrer et jamais sortir, car il faudrait pour cela dépasser la vitesse de la lumièrevitesse de la lumière. On le décrit parfois comme une membrane que l'on ne peut traverser que dans un seul sens et comme toutes les membranes c'est en fait un objet dynamique qui peut vibrer, se déformer, s'étirer mais qui aurait la particularité de ne jamais pouvoir se déchirer.
L'entropie et la théorie de l'information paradoxale des trous noirs
Mais selon les calculs d'Hawking, en décrivant quantiquement le comportement de la lumière et de la matièrematière autour d'un trou noir, ces objets très compacts se mettraient à rayonner comme le ferait un corps chauffé, plus précisément ce que l'on appelle un corps noir. Or, selon la théorie de la thermodynamiquethermodynamique ce rayonnement implique qu'un trou noir possède une quantité que l'on appelle l'entropieentropie. Dans tous les systèmes physiques connus, une grande entropie est associée à un objet très complexe dans le sens où il est constitué de très nombreuses particules décrites par un très grand nombre de paramètres et dont on devrait disposer d'un grand nombre d'informations pour les caractériser. Quand un gazgaz tombe dans un trou noir, cette information n'est plus disponible pour un observateur extérieur. Impossible aussi pour les mêmes raisons de communiquer avec une sonde qui traverserait l'horizon et d'avoir des informations précieuses sur ce que verrait cette sonde puisqu'elle ne pourrait pas envoyer des ondes radio à l'extérieur du trou noir - de plus toute information contenue uniquement dans la mémoire de cette sonde serait irrémédiablement perdue puisque incommunicable à l'extérieur du trou noir.
Dans cette vidéo, Jean-Pierre Luminet nous parle de l'évaporation des trous noirs via le rayonnement de Hawking. Cette évaporation pose une énigme connue sous le nom de paradoxe de l'information avec la physique des trous noirs. © Du Big Bang au vivant
En pratique donc, depuis la définition de l'information et de l'entropie donnée à partir des travaux de Claude Shannon et de John von NeumannJohn von Neumann, la perte d'information engendrée par l'horizon des événements se traduit par une entropie. Hawking, en particulier, avait montré avant sa découverte du rayonnement des trous noirs que la surface de l'horizon des événements devait croître quand un trou noir avale quelque chose et cela en plein accord avec la loi de la croissance de l'entropie de la thermodynamique si l'on identifiait la valeur de l'entropie d'un trou noir au produit de la surface de son horizon par une constante de proportionnalité appropriée.
En ayant les déclarations de Chandrasekhar à l'esprit, on comprend tout de suite que quelque chose ne va pas. Les trous noirs sont caractérisés rigoureusement par un petit nombre de paramètres, la masse, le moment cinétiquemoment cinétique et la charge, indépendamment du fait que l'objet d'une masse donnée qui tomberait dedans soit un bloc de ferfer ou un livre contenant bien plus d'informations.
En conséquence, les trous noirs ne devraient pas pouvoir contenir beaucoup d'information et une partie ne serait pas simplement cachée mais détruite, ou pour le moins c'est ce que l'on pourrait naïvement en déduire de prime abord de sorte que les trous noirs ne devraient pas pouvoir être dotés d'une forte entropie d'une façon cohérente avec les principes fondamentaux de la physique connue, contrairement à ce qu'impliquent les lois de la thermodynamique et de la mécanique quantiquemécanique quantique appliquée à ces objets, issues de la théorie de la relativité générale d'Einstein.
Nous sommes donc confrontés à un paradoxe qui est précisément celui de l’information avec des trous noirs. Il devrait exister des paramètres cachés en très grand nombres derrière le petit nombre de paramètres décrivant un trou noir et les solutions de la théorie d'Einstein ne serait donc que des descriptions artificiellement simplifiées d'un système physique qui pourrait contenir autant de degrés de libertés (positions et vitesses de particules) qu'un gaz comme disent les physiciens dans leur jargon. Les trous noirs ne devraient donc pas être des objets parfaitement "lisses" et simples de la même façon que la Terre n'est pas une sphère de matière parfaitement sphérique et constituée d'un matériaumatériau simple et homogène.
Depuis presque une décennie, l'étude de ce paradoxe a conduit à de nouveaux problèmes dont l'un a été débusqué par Ahmed Almheiri, Donald Marolf, Joseph Polchinski et James Sully. Il est connu sous le nom de controverse du « pare-feupare-feu » (firewallfirewall en anglais). Futura a consacré les deux précédents articles, ci-dessous, à sa résolutionrésolution de sorte que nous ne la détaillerons pas et qu'il sera utile au lecteur pour la suite de s'y référer avant de continuer, mais pas forcément en première lecture.
Il suffit en effet de savoir que l'une des solutions à ce paradoxe est d'admettre que les trous noirs se comportent bel et bien dans beaucoup de situations astrophysique et physique comme s'ils possédaient en pratique un horizon des événements, mais que dans l'absolu ce n'est pas vrai. Un horizon des événements ne serait que ce qu'on appelle en physique un concept effectif et pas fondamental, tout comme il est pratique de considérer que l'eau ou l'airair sont des fluides continus permettant des calculs avec les équationséquations de Navier-Stokes, alors qu'en réalité nous savons bien qu'ils sont formés de moléculesmolécules.
Un gaz de surpercordes autogravitant
On a souvent avancé qu'une théorie quantique de la gravitationgravitation et de son couplage à la matière permettrait de résoudre toutes les questions laissées en suspens avec les trous noirs, en supprimant notamment les singularités au cœur des solutions de trous noirs connues en relativité générale. Depuis des années, des physiciens et en particulier Samir Mathur de l'université d'État de l'Ohio ont avancé que ce doit effectivement être le cas en utilisant la théorie de supercordes laquelle impliquerait qu'au-delà du stade d'effondrementeffondrement d'une étoile à neutronsétoile à neutrons devenant un trou noir, l'objet un peu plus compact formé serait en fait une boule de supercordes baptisée « fuzzballs » en anglais, une théorie que l'on doit précisément à Samir Mathur.
Si l'on suppose que les particules de matière et même toutes les particules quantiques fondamentales, gluonsgluons et bosonsbosons de Brout-Englert-Higgs inclus, sont des supercordes vibrantes, alors les calculs montrent que la matière d'une étoile s'effondrant sans recours sous l'horizon des événements associée au trou noir qu'elle semble devenir ne devrait pas finir sous la forme d'un point de densité infini au lieu où l'espace-temps lui-même s'anéantit selon la théorie non quantique d'Einstein, au cœur d'un trou noir. Les supercordes quantiques s'étireraient et s'allongeraient au point de former une sorte de gaz quantique diffusdiffus occupant tout le volumevolume à l'intérieur d'un horizon des événements qui ne serait qu'effectif, un peu comme l'est ce qui tient lieu de surface pour le SoleilSoleil.
Mais comment tester une telle théorie ?

Des modes quasi-normaux caractéristiques des trous noirs
Le signal des ondes gravitationnelles détectées par Ligo et Virgo concernant des collisions de trous noirs était déjà un argument fort en faveur de l'existence des trous noirs de la théorie de la relativité générale mais il n'est pas encore à ce jour complètement probant. En fait, ce que l'on essaie vraiment de mettre en évidence au fur et à mesure que ces détecteurs, et d'autres comme Kagra, vont monter en sensibilité, c'est ce que l'on appelle les modes quasi-normaux de l’horizon des événements des trous noirs et on dispose d'ores et déjà d'indices en ce sens.
Les modes quasi-normaux sont déjà connus en physique classique avec des cloches que l'on frappe. Il se produit un son qui s'amortit avec le temps et ce son peut se décomposer en plusieurs fréquencesfréquences et ondes élémentaires particulières, analogue à des modes normaux composant une corde vibrante sans amortissement notable. Ces modes quasi-normaux constituent des sortes de cartes d'identité spectrales d'un trou noir en espace-temps courbe tout comme le spectrespectre lumineux des éléments pour la composition des atmosphèresatmosphères des étoiles.
Or, comme on l'a dit, un horizon des événements peut se comporter comme une membrane vibrante et il est donc en théorie possible de démontrer l'existence de cette membrane avec ses modes de vibrationvibration propres, les modes quasi-normaux, en analysant le signal gravitationnel d'une collision de trou noir. C'est un peu comme si on entendait le "son" du trou noir et que l'on vérifiait qu'il se comporte bien comme ce que l'on attendrait d'un trou noir.
Dans l'article qui vient d'être publié, étant donné la complexité des calculs avec la théorie des fuzzballs, les chercheurs ont voulu faire un test plus simple concernant la collision de deux de ces boules de cordes et avoir une idée du signal gravitationnel produit. Ils ont fait des simulations numériquessimulations numériques concernant le comportement d'un espace-temps décrit par une théorie de supergravitésupergravité en quatre dimensions dite de type N=2 et capturant la géométrie d'une solution de type fuzzball pour ce qui serait un trou noir effectif extérieurement perturbé.
Les calculs montrent alors qu'initialement le signal obtenu est semblable à celui des modes quasi-normaux d'un trou noir nouvellement formé par la fusionfusion de deux trous noirs en collision, mais au bout d'un certain temps le signal ne comporte plus les modes décrivant un horizon et trahit donc le fait qu'il n'est qu'effectif. En bonus, les mêmes calculs montrent que l'on pourrait aussi mettre en évidence des échos gravitationnels, un phénomène décrit dans le précédent article ci-dessous, et proviendrait ici des ondes gravitationnelles se propageant à l'intérieur de la boule de supercordes.
Selon les chercheurs, Ligo et Virgo devraient un jour être en mesure de détecter ce signal.
Des traces des trous noirs quantiques de Hawking dans les ondes gravitationnelles ?
Article de Laurent SaccoLaurent Sacco publié le 24/01/2020
Selon deux physiciens, un traitement quantique de l'horizon des trous noirs, pouvant aider à comprendre les énigmes posées par les trous noirs quantiques de Hawking, pourrait conduire à une signature du comportement quantique de l'horizon des événements dans les ondes gravitationnelles. Ligo et Virgo pourraient avoir déjà détecté des indices de cette signature avec la source d'onde GW170817.
On ne le répétera sans doute jamais assez mais un trou noir ne se définit ni par sa densité ni par le fait qu'il posséderait une singularité de l'espace-temps en son cœur. Les trous noirs supermassifstrous noirs supermassifs possèdent des densités qui peuvent être celle de l'eau ou de l'air, et une théorie quantique de la gravitation supprime très probablement l'effondrement de la matière, de la lumière et finalement, de l'espace-temps lui-même au point de devenir une singularité, tout comme les lois quantiques stoppent l'effondrement des électronsélectrons sur les noyaux des atomesatomes malgré l'attraction électrostatiqueélectrostatique entre ces particules.
Ce qui définit un trou noir de façon rigoureuse -- depuis notamment les travaux de Roger PenroseRoger Penrose, Stephen HawkingStephen Hawking, John Wheeler et d'autres chercheurs des années 1960 --, c'est l'existence d'un horizon des événements clos entourant une région de l'espace. Il existe une formulation très précise de la nature de cet horizon mais, grossièrement, on peut dire que, dans le cadre d'une théorie classique de la gravitation avec un espace-temps courbe (il n'est pas nécessaire de supposer que les équations d'Einstein soient les bonnes équations pour décrire la dynamique de cet espace-temps complètement), un trou noir est une sorte de bulle formée d'une membrane fictive, effective, qui ne laisse passer matière et lumière que dans un seul sens. Une fois dans la bulle, elles ne peuvent plus en sortir car le champ de gravitation nécessiterait qu'un objet physique, particule ou onde, puisse se propager parfois plus vite que la lumière.
On sait que Stephen Hawking, en se basant notamment sur les travaux de Jacob Bekenstein, Yakov Zel'dovich et Alexei Starobinski, a été conduit à découvrir que la mécanique quantique impliquait que les trous noirs, en rotation ou pas, devaient tout de même s'évaporer en perdant leurs masses et leurs moments cinétiques s'ils en avaient. Un trou noir doit, en effet, émettre un rayonnement chaud du type de celui d'un corps noir avec une température inversement proportionnelle à sa masse. En clair, plus un trou noir devient petit, plus il devient chaud et plus il s'évapore vite.
L'horizon des événements pose un problème avec l'information quantique
La découverte du rayonnement Hawking a ensuite conduit à l’énigme du paradoxe de l’information, là aussi une découverte du défunt Stephen Hawking. Si la mécanique quantique force un trou noir à rayonner, son évaporation et l'existence d'un horizon des événements devraient conduire à la destruction de l'information qui était portée par les objets tombants dans un trou noir. Tout le contenu en information d'un livre comme l'HypérionHypérion de Friedrich Hölderlin devrait disparaître à tout jamais dans un trou noir et seule sa masse ne pourra en sortir et que sous la forme de l'énergieénergie et des particules du rayonnement Hawking.
Malheureusement, cette destruction d'information est interdite par la mécanique quantique. Il y a une erreur mais où ?
Or, au début des années 2010, en poursuivant leur étude de cette énigme, les théoriciens sont tombés sur des contradictions encore plus graves qui ont conduit certains d'entre eux à remettre en question la notion classique de l'horizon d'un trou noir en invoquant, par exemple, l'existence d'un « pare-feu » (firewall en anglais). Une intense controverse s'ensuivit conduisant Stephen Hawking à faire sans doute un peu malicieusement son buzz habituel en suggérant effectivement que les trous noirs, au sens habituel, n'existaient pas et que l'horizon des événements n'était qu'une approximation commode pour comprendre certains phénomènes mais n'existait pas vraiment.
Futura avait consacré un précédent article à cette polémique que le lecteur peut trouver ci-dessous pour en apprendre beaucoup plus.
Toujours est-il que l'idée que l'horizon des événements classique ne soit pas vraiment là -- à cause d'effets quantiques par exemple si l'on introduit la théorie des supercordesthéorie des supercordes pour décrire les trous noirs comme des sortes de « pelotes de cordes » baptisées des « fuzzballs » en anglais, une théorie que l'on doit au physicien théoricien Samir Mathur de l'université d'État de l'Ohio --, est toujours bien présente à l'esprit des chercheurs. Il existe même des alternatives plus radicales comme la théorie des gravastars qui suppose qu'un tout autre objet apparaît lors de l'effondrement des étoiles, un objet avec une sorte de coque solidesolide presque à la place de cet horizon. Mais comment le démontrer ou au contraire le réfuter ?
L'essor de l'astronomie gravitationnelle est peut-être en train de changer la donne avec la possible détection des modes quasinormaux des trous noirs, comme l'expliquait OlivierOlivier Minazolli à Futura, et même les images de trous noirs qui peuvent être fournies via l'Event Horizon Telescope comme l'expliquait également à Futura Aurélien Barrau. Le regretté Pierre Binetruy parlait déjà il y a quelques années, comme le montre la fin de la vidéo ci-dessus, de pouvoir tester des théories quantiques des trous noirs avec les ondes gravitationnelles.
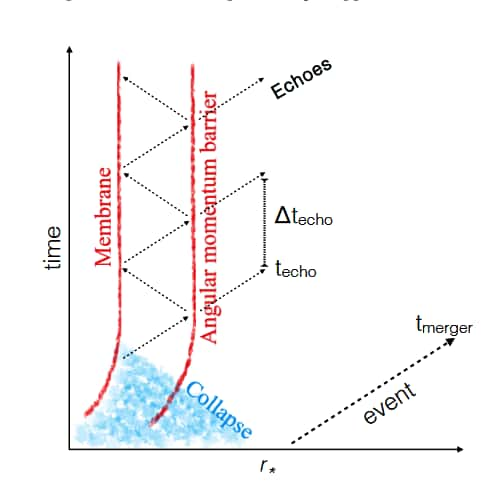
Des ondes gravitationnelles qui rebondissent entre deux barrières
C'est donc avec un certain intérêt que l'on prend connaissance de l'article d'une équipe de chercheurs composée de Jahed Abedi, chercheur postdoctoral au Max PlanckMax Planck Institute for Gravitational Physics (Albert Einstein Institute en Allemagne), et de Niayesh Afshordi (de l'université de Waterloo et de l'Institut Périmètre de physique théorique au Canada). Disponible en accès libre sur arXiv, il a été publié dans le Journal of Cosmology and Astroparticle Physics et a même été récompensé par un prix, le Buchalter Cosmology Prize.
L'idée est la suivante : On part de l'hypothèse que l'horizon des événements d'un trou noir est modifié par des effets quantiques ou une nouvelle physique. Mais dans les deux cas, ils font tout de même en sorte que l'extérieur du nouvel objet se comporte toujours à bien des égards comme un trou noir en rotation ordinaire. On peut donc toujours montrer que des ondes, notamment gravitationnelles mais aussi celles émises par l'évaporation quantique d'un trou noir, vont rencontrer une sorte de murmur, une barrière, produite par la structure de l'espace-temps mais un peu au-delà de la région où se trouverait un horizon quantique ou ce qui remplace l'horizon des événements standard (pour les initiés voir l'équation de Klein-Gordon tout en bas de l'article).
Si l'on prend l'analogieanalogie avec un son, alors une partie des ondes émises par le trou noir ou ce qui en tient lieu, va traverser le mur et une autre va être réfléchie. L'énergie des ondes initiales étant répartie entre ces deux parties. Mais si le lieu de l'horizon des événements se comporte en fait aussi comme un mur partiellement réfléchissant, en raison précisément d'effets quantiques ou d'une nouvelle physique, alors les ondes vont rebondir entre les deux murs et un signal périodique -- bien que de plus en plus faible à cause du partage de l'énergie en ondes transmises et réfléchies -- va se présenter comme une sorte d'écho si l'on prend le cas des ondes gravitationnelles.
On peut en effet appliquer ce scénario au cas de la source d'ondes baptisée GW170817, issue de la fusion de deux étoiles à neutrons, et qui a été détectée le 17 août 2017 par Ligo et Virgo. Le trou noir qui a dû se former lors de la fusion de ces deux astresastres compacts a dû produire des ondes pendant un certain temps, comme le ferait une cloche dont les vibrations s'amortissent après un choc.
Dans leur article primé, Jahed Abedi et Niayesh Afshordi annoncent (bien que la preuve convaincante ne soit pas encore là) que, selon leurs analyses encore embryonnaires, on commencerait à voir des indices de la présence de ces échos gravitationnels dans le signal détecté pour GW170817.
La prudence s'impose mais les conclusions qu'en tire Niayesh Afshordi semblent raisonnables : « Nos résultats sont encore provisoires ; il y a encore une petite chance que ce que nous voyons soit dû à un bruit aléatoire dans les détecteurs, mais cela deviendra de moins en moins probable au fur et à mesure si nous trouvons plus de cas de ce genre. Maintenant que les scientifiques savent ce que nous recherchons, nous pouvons guetter d'autres exemples et obtenir une confirmation beaucoup plus solide de ces signaux. Une telle confirmation serait la première sonde directe de la structure quantique de l'espace-temps ».
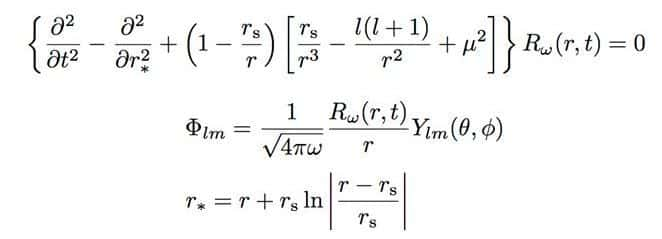
Trous noirs : Stephen Hawking remet-il en cause leur existence ?
Article de Laurent Sacco publié le 30/01/2014
Stephen Hawking avait déjà fait sensation il y a 40 ans en annonçant que les trous noirs ne piégeaient pas de l'énergie pour toujours et qu'ils pouvaient s'évaporer. Il s'agissait d'une conséquence des lois de la mécanique quantique. Il jette à nouveau le trouble en suggérant que les trous noirs n'existent pas. Mais est-ce vraiment ce qu'il affirme ? L'information ayant suscité des réactions et des affirmations parfois fantaisistes, la réponse mérite une analyse fine...
Stephen Hawking vient de réaliser un nouveau coup d'éclat médiatique dont il a le secret. On se souvient par exemple il y a quelques années des remous qu'il avait causés avec le boson de Brout-Englert-Higgs. Ses travaux sur la théorie des trous de ver l'avaient conduit à douter de la possibilité de découvrir cette fameuse particule au LHCLHC. Il avait donc parié avec le physicien Gordon Kane qu'on ne l'observerait pas.
Cette année, deux semaines après son anniversaire, Hawking a déposé sur arxiv un article court et sans équations dans lequel il semble affirmer que les trous noirs n'existent pas. En réalité, le contenu de cet article a déjà été exposé sur Skype en août 2013, devant ses collègues, lors d'un colloque du Kavli Institute for Theoretical Physics, à Santa Barbara (Californie). Il concerne une solution à une énigme découverte il y a environ deux ans par Ahmed Almheiri, Donald Marolf, Joseph Polchinski et James Sully (AMPS) en réfléchissant au fameux paradoxe de l'information avec les trous noirs. Il s'agit donc d'un nouveau rebondissement dans la saga du problème du corps noircorps noir, liant de façon étroite la mécanique quantique, la relativité générale et la thermodynamique.
Présenté par Hubert Reeves et Jean-Pierre Luminet, Du Big Bang au vivant est un projet multiplateforme qui couvre les plus récentes découvertes dans le domaine de la cosmologie. Jean-Pierre Luminet explique ici l'histoire des découvertes théoriques des trous noirs. © Du Big Bang au vivant
Les travaux de Hawking sur la théorie des trous noirs, aussi bien du point de vue de la relativité générale classique qu'en utilisant les lois de la mécanique quantique, sont au cœur du paradoxe découvert par AMPS. Quelques rappels sur la théorie classique et quantique des trous noirs sont indispensables pour comprendre en quoi consiste ce paradoxe. Ils permettent aussi de prendre du recul par rapport aux déclarations récentes de Stephen Hawking.
L'effondrement gravitationnel des étoiles
Pendant longtemps, la communauté scientifique n'a pas pris au sérieux l'existence des objets que l'on appelle aujourd'hui des trous noirs, et qui étaient prédits par les équations de la relativité générale d'Einstein. Les choses ont commencé à changer quand au début des années 1960, une équipe aux États-Unis (un trio de physiciens qui avaient été impliqués dans la conception de la bombe H états-unienne) s'est attelée à un problème de simulation numérique bien précis. Michael Mayn, Richard White et Stirling Colgate ont mis à profit les compétences qu'ils avaient acquises en physique nucléaire, mécanique des fluides et théorie du transfert radiatif pour simuler sur ordinateurordinateur l'implosion d'une étoile de façon réaliste. Il s'agissait de vérifier les conclusions découlant des calculs simplifiés conduits par Robert Oppenheimer et Hartland Snyder à la fin des années 1930.
Presque au même moment, dans l'ex-URSS, l'un des concepteurs de la bombe H soviétique, le grand Yakov Zel'dovich, lance trois de ses collègues sur le même problème. Les deux équipes ont abouti à des résultats identiques. Au-dessus d'une certaine masse, rien ne peut plus stopper la contraction gravitationnelle d'une étoile, qui finit par franchir une surface sphérique dont la taille est donnée par le rayon de Schwarzschildrayon de Schwarzschild. L'état final de la matière sous cette surface restait cependant problématique. Les calculs menés avec la relativité générale semblaient impliquer que la courbure de l'espace-temps augmentait en même temps que la densité de la matière pour finir par atteindre une valeur infinie : une singularité.
En 1965, le mathématicienmathématicien Roger Penrose démontra que ce devait bien toujours être le cas dans le cadre de la relativité générale classique. Il suffisait de postuler des conditions très plausibles concernant l'état de la matièreétat de la matière sous la surface, que l'on appelle maintenant l'horizon des événements, c'est-à-dire une région de l'espace-temps dont on ne peut s'échapper même à la vitesse de la lumière.
Trou noir et horizon des événements
Il était déjà clair à ce moment-là, notamment pour le grand John Wheeler, qu'avant d'atteindre la courbure infinie prédite par le théorèmethéorème de singularité de Penrose, la mécanique quantique devait entrer en ligne de compte au niveau de l'espace-temps lui-même. Elle devait probablement supprimer la singularité, comme elle avait stoppé l'effondrement des électrons sur le noyau de l'atome dans le modèle de Rutherford.
Du point de vue de la relativité générale, on pouvait développer une théorie précise des singularités gravitationnelles, mais nul doute que l'état final de l'implosion d'une étoile ne serait connu que lorsqu'on disposerait d'une théorie quantique de la gravitation et même d'une théorie unifiée des forces et de la matière. En pratique, l'espace-temps d'une étoile s'effondrant, ou de toute autre masse de matière suffisamment comprimée, évoluait jusqu'à un état d'équilibre final identique pour un observateur extérieur à ce qu'on appelle la solution de Schwarzschild décrivant un trou noir statique et éternel. La singularité centrale de cette solution devait être une description idéalisée et non physique d'une région extrêmement dense dominée par des effets quantiques.

On pouvait donc se contenter de développer pour l'astrophysique une théorie des astres complètement effondrés gravitationnellement en se basant sur la solution idéalisée de Schwarzschild. On avait donc défini ce qui est maintenant appelé un trou noir non par le fait qu'il contiendrait une vraie singularité de l'espace-temps et des équations décrivant le comportement de la matière, mais par l'existence d'un horizon des événements. Stephen Hawking, notamment, s'est beaucoup appuyé sur les propriétés de la surface que constitue l'horizon des événements pour explorer la physique des trous noirs. Cette surface définissant une région dont plus aucune information ne peut émerger en physique classique, on peut lui associer une entropie, puisque, en pratique ou de manière absolue, elle rend indisponible pour un observateur extérieur l'information contenue dans un objet ayant traversé l'horizon.
Des trous noirs quantiques qui rayonnent
Toutefois, au voisinage de l'horizon, comme partout dans le vide, des paires de particules apparaissent et disparaissent du fait des lois de la mécanique quantique. Les forces de maréeforces de marée exercées par le trou noir peuvent séparer ces particules, de sorte que l'une tombe parfois dans le trou noir et l'autre s'échappe vers l'infini. L'énergie utilisée pour séparer ces paires étant prise au trou noir, sa masse diminue et cette perte se retrouve associée à l'énergie portée par la particule rayonnée par le trou noir. Comme Hawking allait le montrer pendant les années 1970, tout se passe donc comme si un trou noir se mettait à rayonner comme un corps noir en s'évaporant. Le rayonnement thermiquerayonnement thermique du corps noir étant très désordonné, l'évaporation d'un trou noir semblait détruire de l'information. L'énergie d'un livre jeté dans un trou noir finirait par en ressortir, mais l'information qu'il portait serait perdue à jamais du fait de l'existence d'un horizon des événements.
Pour Leonard Susskind et Gerard 't Hooft, cela devait être impossible, car cela conduisait à violer les lois de la mécanique quantique. Hawking en était bien conscient et il pensait justement avoir découvert une clé pour aller au-delà de ces lois. Mais pendant les années 1990, la seconde révolution de la théorie des cordesthéorie des cordes, et notamment la fameuse correspondance AdS/CFT (encore appelée conjecture de Maldacena) allait changer tout cela. Confirmant l'idée de 't Hooft et Susskind qu'une théorie de la gravitation quantiquegravitation quantique devait faire apparaître des phénomènes ressemblant à ceux associés à des hologrammes, cette correspondance impliquait avec force que les lois de la mécanique quantique étaient bien respectées par l'évaporation d'un trou noir. On pouvait considérer d'une certaine façon que les paires de particules à l'origine de l'évaporation d'un trou noir étaient intriquées. De sorte que l'information initialement contenue par celui-ci était, grâce à l'intrication quantiqueintrication quantique, tout de même libérée et présente dans le rayonnement, bien que celui-ci apparaisse très désordonné pour un observateur extérieur.
Dans cette vidéo, Jean-Pierre Luminet nous parle de l'évaporation des trous noirs via le rayonnement de Hawking. Cette évaporation pose une énigme connue sous le nom de paradoxe de l'information avec la physique des trous noirs. © Du Big Bang au vivant
Revenons maintenant vers le paradoxe découvert par Ahmed Almheiri, Donald Marolf, Joseph Polchinski et James Sully. Il est connu depuis environ deux ans sous le nom de controverse du « pare-feu » (firewall en anglais). Il fait toujours l'objet de nombreuses discussions entre physiciens théoriciens, car il en rend perplexes plus d'un qui avouent être plutôt dans la confusion à son sujet.
Des particules maximalement intriquées
Pour le comprendre, il faut savoir qu'il existe différents degrés d'intrication quantique entre systèmes physiques. Il y a notamment ce qu'on appelle l'intrication maximale, qui affirme que lorsque deux systèmes sont maximalement intriqués, on ne peut plus les intriquer avec un troisième. Rien n'interdit une intrication entre plus de deux systèmes, mais elle n'est alors plus maximale. La mécanique quantique implique que si on attend suffisamment longtemps, une duréedurée appelée le temps de Page (en référence au physicien Donald Page), le rayonnement passé émis par un trou noir avant ce temps sera maximalement intriqué avec le rayonnement émis après ce temps.
Si un objet est jeté dans le trou noir après ce temps de Page, il devrait aussi être intriqué avec le rayonnement passé et futur du trou noir en contradiction avec le fait qu'ils sont déjà maximalement intriqués. Si l'on refuse de modifier les lois de la mécanique quantique, il semble qu'il faille interdire à l'objet de pénétrer dans le trou noir.
Un pare-feu en contradiction avec la relativité générale
AMPS est arrivé à la conclusion que juste au niveau de l'horizon d'un trou noir, l'objet en chute libre devait rencontrer un intense flux d'énergie, un pare-feu, le mettant en pièces et l'empêchant de pénétrer dans le trou noir. Ce scénario pose problème : pour des trous noirs d'assez grande taille, comme un trou noir supermassif contenant des milliards de masses solaires, il n'y a aucune raison pour qu'un observateur en chute libre remarque quoi que ce soit au voisinage de l'horizon. Les forces de marée sont très faibles et il n'y a pas de rayonnement quantique pour un tel observateur en chute libre. Qui plus est, un tel trou noir apparaît comme très froid pour un observateur extérieur même, dans cette situation, au temps de Page. C'est en réalité une conséquence du principe d'équivalence de la relativité générale, sur lequel elle repose lourdement. Le message semble clair : si on refuse de toucher à la théorie quantique, il faut un pare-feu, mais celui-ci entre en contradiction avec la relativité générale...

Voilà l'endroit où nous allons rejoindre Stephen Hawking... Si on ne change par les principes de la mécanique quantique et qu'on ne touche pas à ceux de la relativité générale, il faut peut-être modifier légèrement la théorie des trous noirs. Hawking propose donc de remettre en cause le caractère absolu de l'horizon des événements, ce qui permettrait de se passer d'un pare-feu tout en conservant les lois de la mécanique quantique. En pratique, l'horizon ne définirait pas une région dont la lumière ne pourrait pas s'échapper, mais une région où elle serait piégée comme la matière pendant un temps assez long.
Hawking ne rejette donc pas en bloc ses travaux ni les trous noirs, il parle de l'existence d'un horizon apparent, effectif, comme l'est la description continue d'un fluide par les équations de Navier-Stokes. Hawking propose d'ailleurs de reconsidérer un trou noir comme une sorte d'état lié du champ de gravitation, turbulent et chaotique. La perte apparente d'information donnant lieu à l'existence d'une entropie associée à la surface définie par l'horizon des événements serait donc analogue à celle connue en physique classique pour une collection de particules, un artefact d'une description macroscopique simplifiée.
Chaos, turbulence et trous noirs
L'article de Hawking laisse ses collègues quelque peu perplexes, et même dubitatifs, même si Hawking fait bien allusion à la correspondance de Maldacena posant qu'à la frontière d'un espace-temps AdS, un fluide quantique, ressemblant à un plasma de quarksquarks et de gluons (conformément au principe holographique) reflète le comportement d'un trou noir en train de s'évaporer. Elle suggère que l'effondrement chaotique de la matière donnant un trou noir serait relié à un état turbulent de ce fluide. Mais cette connexion reste floue dans les propos de Hawking.
Lorsqu'il parle d'un état chaotique classique de l'espace-temps et de la matière sous l'horizon apparent d'un trou noir, on peut se demander s'il n'a pas en tête une connexion explorée depuis quelques années entre la théorie des trous noirs et celle des fluides turbulents. Il s'agit de la correspondance fluide-gravité, qui utilise la correspondance AdS/CFT pour traduire des problèmes de la dynamique des fluides en problèmes de relativité générale.
Ce qui est sûr, c'est que Stephen Hawking compare la perte effective d'information et de prédictibilité dans un trou noir avec l'impossibilité de prédire la météométéo à long terme. En principe, nous dit la physique classique, le fluide que constitue l'atmosphère a un comportement déterministe, mais en pratique, on perd rapidement de l'information sur lui et on ne peut plus faire de prédictions précises. On pourrait donc, par analogie, concevoir un trou noir comme une boule de fluide très dense, chaotique et turbulente, mais qui finit par s'évaporer.
Les nouveaux trous noirs, des boules de supercordes ?
Une telle description n'est pas radicalement nouvelle. John Wheeler utilisait dès les années 1950 et 1960 des images issues de l'hydrodynamique pour se représenter la physique de l'espace-temps. On peut penser aussi au paradigme de la membrane développé pendant les années 1970 et 1980 par Kip Thorne et Thibault DamourThibault Damour. En effet, pour les besoins de l'astrophysique, par exemple pour étudier les quasars, on peut remplacer la description d'un trou noir avec son horizon par celle d'une sorte de bulle de fluide visqueux douée de propriétés électriques et thermodynamiques. On n'a pas à se soucier de ce qu'il y a à l'intérieur de cette bulle, qui se comporte donc comme un horizon apparent.

On peut finalement se demander si la solution que propose Hawking au paradoxe du pare-feu mis en évidence par AMPS n'a pas déjà été donnée dans le cadre de la théorie des cordes par le physicien théoricien Samir Mathur de l'université d'État de l'Ohio. Il a proposé voilà une dizaine d'années que les trous noirs étaient des sortes de « pelotes de cordes » qu'il a baptisées des « fuzzballs » en anglais. Selon ses calculs, en tenant compte du fait que les particules seraient en réalité des cordes, une fois qu'elles ont pénétré dans un trou noir, elles se mettraient en quelque sorte à s'étaler jusqu'à occuper tout l'intérieur de la région sous l'horizon d'un trou noir. Si le trou noir est petit, l'image qui émerge est celle d'une sorte d'équivalent d'une étoile à neutrons très dense, mais cette fois constituée de cordes quantiques. L'essentiel de ce que contient la théorie standard des trous noirs serait conservé, mais l'horizon des événements serait bien effectif, apparent, exactement comme le propose Hawking. Mathur vient d'ailleurs de publier récemment des articles dans lesquels il affirme que si la description des trous noirs en termes de fuzzballs est bien correcte, on conserve la thermodynamique des trous noirs standard et la théorie quantique tout en résolvant le paradoxe de l'information et sans avoir besoin de pare-feu.
Une chose est sûre : les trous noirs sont encore loin d'avoir fini de susciter des énigmes, et ils sont une extraordinaire fenêtrefenêtre sur la physique la plus fondamentale de l'univers.
Futura dans les Étoiles - Podcast
---
Futura dans les Étoiles, c'est le rendez-vous incontournable des amateurs d'astronomie et d'espace. Tous les 1ers du mois, retrouvez-nous pour un tour complet des éphémérides du mois, avec des conseils pour observer au mieux ce qu'il se passe dans le ciel. Un épisode spécial publié tous les 15 du mois vous proposera d'en apprendre plus sur un objet ou un événement particulier qui marquera l'actualité astronomique et spatiale.
---